- •Глава II. Дифференциальное исчисление функций одной переменной
- •2.1. Производная функции
- •2.1.1. Определение производной функции
- •2.1.2. Дифференцируемость функции, ее взаимосвязь с производной и непрерывностью функции
- •2.1.3. Непосредственное нахождение производной
- •2.1.4. Геометрический смысл производной
- •2.1.5. Механический смысл производной
- •2.1.6. Правила дифференцирования функций
- •2.1.7. Вывод производных основных элементарных функций
- •2.1.8. Сводка формул Правила дифференцирования
- •2.1.9. Производные высших порядков
- •2.1.10. Эластичность функции
- •2.1.11. Геометрический смысл эластичности
- •2.1.12. Экономический смысл эластичности
- •2.1.13. Свойства эластичности функции
- •2.2. Дифференциал функции одной переменной
- •2.2.1. Определение дифференциала функции
- •2.2.2. Геометрический смысл дифференциала
- •2.2.3. Свойства дифференциала
- •2.2.4. Применение дифференциала для приближенных вычислений
- •2.2.5. Дифференциалы высших порядков
- •2.3. Теоремы о дифференцируемых функциях
- •2.3.1. Теорема Ролля
- •2.3.2. Геометрический смысл теоремы Ролля
- •2.3.3. Примеры использования теоремы Ролля
- •2.3.4. Теорема Лагранжа о конечном приращении функции
- •2.3.5. Геометрический смысл теоремы Лагранжа
- •2.3.6. Теорема Коши
- •2.3.7. Раскрытие неопределенностей при нахождении пределов. Правило Лопиталя
- •2.3.8. Применение правила Лопиталя для раскрытия неопределенностей типа степени
- •2.4. Формулы Тейлора и Маклорена
- •2.4.1. Формула Тейлора. Остаточный член в форме Лагранжа
- •2.4.2. Формула Маклорена
- •2.4.3. Разложение основных элементарных функций по формуле Маклорена
- •2.4.4. Применение формулы Маклорена для вычисления пределов и значений функций
- •2.5. Исследование функций
- •2.5.1. Необходимый и достаточный признаки монотонности функций
- •2.5.2. Определение экстремума функции
- •2.5.3. Необходимый признак экстремума функции
- •2.5.4. Первый достаточный признак экстремума функции (с использованием первой производной)
- •2.5.5. Второй достаточный признак экстремума функции (с использованием производной второго порядка)
- •2.5.6. Определение выпуклости, вогнутости графика функции, точки перегиба
- •2.5.7. Достаточный признак выпуклости, вогнутости графика функции
- •2.5.8. Необходимый признак существования точки перегиба
- •2.5.9. Достаточный признак существования точки перегиба
- •2.5.10. Асимптоты графика функции
- •2.5.11. Построение графика функции
2.2.5. Дифференциалы высших порядков
Дифференциалом n-го порядка называется дифференциал от дифференциала (n 1)-го порядка, полученный в предположении, что дифференциал независимой переменной постоянный, т. е.
![]() .
.
Находим
![]() ,
,
![]() .
Очевидно,
.
Очевидно,
![]() .
.
Из последнего
равенства можно записать
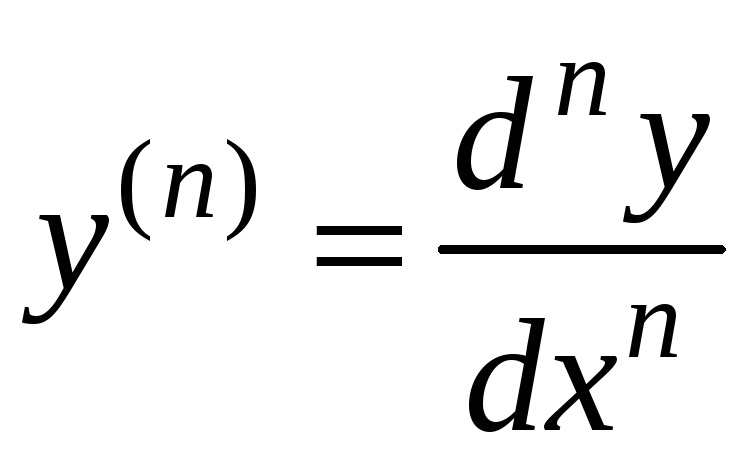 .
.
Пример 2.9. Найти
дифференциал второго порядка функции
![]() .
.
Находим:
![]() ,
,
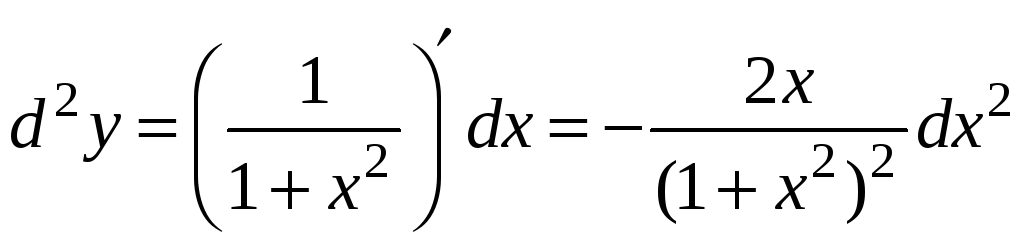 .
.
2.3. Теоремы о дифференцируемых функциях
2.3.1. Теорема Ролля
Теорема Ролля.
Если функция
y
= f(x)
непрерывна на отрезке [a,
b],
дифференцируемая в каждой его внутренней
точке и принимает равные значения в
граничных точках отрезка, то найдётся
такая внутренняя точка отрезка х=
с,
в которой производная функции равна
нулю
![]() .
.
Д о к а з а т е л ь с т в о. Так как функция y = f(x) по условию теоремы непрерывная, то она достигает на отрезке [a, b] наибольшего М и наименьшего m значений, т. е.
![]() ;
;
![]() .
.
Рассмотрим два возможных случая.
1. M
= m.
Если наибольшее М
и наименьшее m
значения
функции совпадают, то она является
постоянной y
= f(x)
= const
и её производная равна нулю в любой
внутренней точке этого отрезка, т. е.
![]() .
.
2. M
m.
Тогда y
= f(x)
не является постоянной и не может
одновременно достигать наибольшего и
наименьшего своих значений в граничных
точках отрезка [a,
b]
. Пусть она достигает наибольшего
значения в некоторой внутренней точке
х =
с,
т. е. f(c)=
M.
В этом случае
![]()
![]() и приращение функции в этой точке
и приращение функции в этой точке
![]()
![]() .
Найдем односторонние пределы функции
в этой точке
.
Найдем односторонние пределы функции
в этой точке
![]() ,
так как
,
так как
![]() ,
,
![]() .
.
![]() ,
так как
,
так как
![]() ,
,
![]() .
.
Функция y
= f(x)
дифференцируемая в каждой внутренней
точке, в том числе и при х
= с.
Следовательно, производная функции в
этой точке равна нулю
![]() .
.
2.3.2. Геометрический смысл теоремы Ролля
|
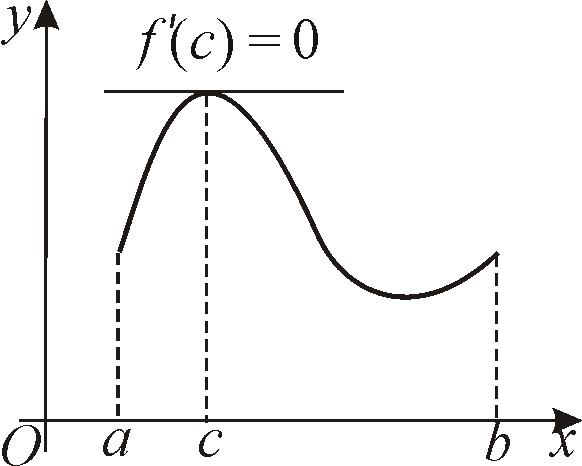
Рис. 23
|
Если график функции y = f(x) непрерывный на отрезке [a, b] и гладкий (не имеет точек излома) на интервале (a, b) и ординаты графика функции в граничных точках отрезка равные f(а)= f(b), то найдется такая внутренняя точка отрезка х = с, в которой касательная параллельна оси Ох (рис. 23).
|
2.3.3. Примеры использования теоремы Ролля
Рассмотрим три функции.
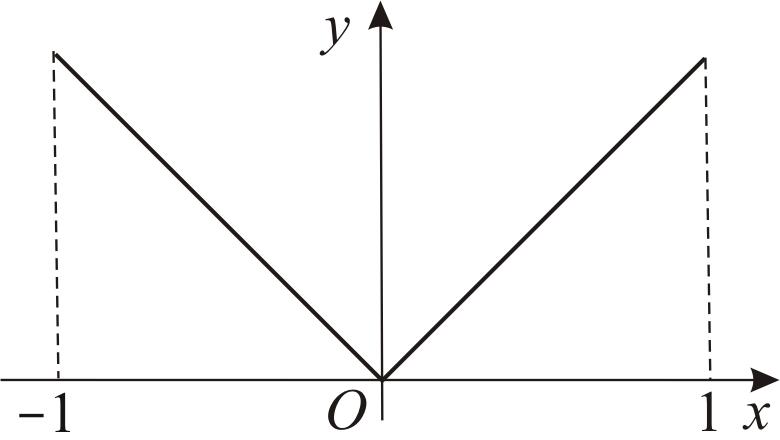
1. Функция
![]() является непрерывной на отрезке [1;
1] и принимает равные значения в граничных
точках
является непрерывной на отрезке [1;
1] и принимает равные значения в граничных
точках
![]() .
Однако функция не имеет производной в
точке х
= 0, так как при х
> 0
.
Однако функция не имеет производной в
точке х
= 0, так как при х
> 0
![]() ,
а при х
< 0
,
а при х
< 0
![]() .
Нарушение условия дифференцируемости
функции только в одной внутренней точке
отрезка приводит в данном случае к
отсутствию точки, в которой производная
функции равна нулю, а касательная к
графику горизонтальна (рис. 24).
.
Нарушение условия дифференцируемости
функции только в одной внутренней точке
отрезка приводит в данном случае к
отсутствию точки, в которой производная
функции равна нулю, а касательная к
графику горизонтальна (рис. 24).
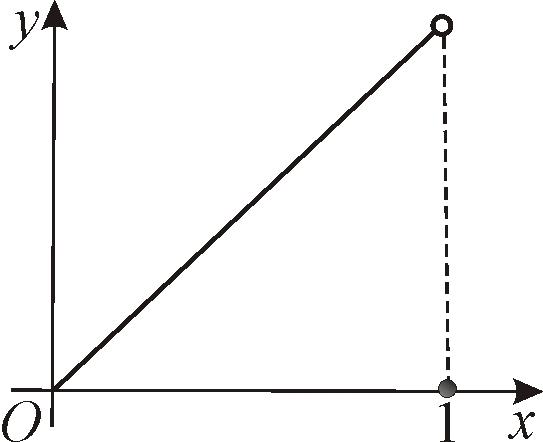
2. Функция
![]() принимает равные значения в граничных
точках рассматриваемого отрезка
принимает равные значения в граничных
точках рассматриваемого отрезка
![]() ,
является дифференцируемой в каждой
внутренней точке отрезка [0; 1], но имеет
одну точку разрыва при х
= 1. В результате этого в данном случае
отсутствует точка, в которой производная
функции равна нулю, а касательная к
графику горизонтальна (рис. 25).
,
является дифференцируемой в каждой
внутренней точке отрезка [0; 1], но имеет
одну точку разрыва при х
= 1. В результате этого в данном случае
отсутствует точка, в которой производная
функции равна нулю, а касательная к
графику горизонтальна (рис. 25).
|
Рис. 24 |
Рис. 25 |
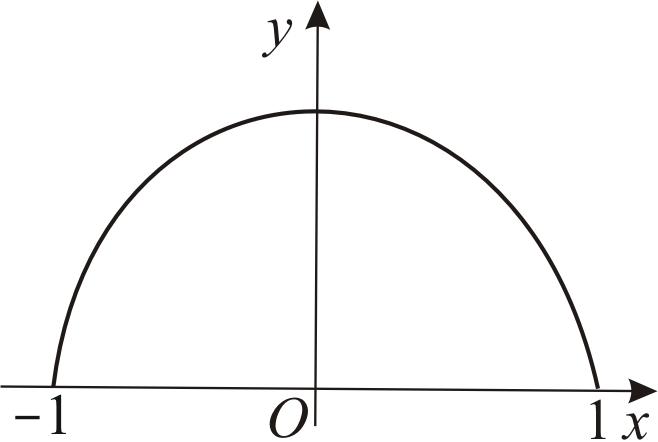
Рис. 26 |
3. Функция
![]() на
отрезке [1;
1] удовлетворяет всем требованиям теоремы
Ролля. Функция является непрерывной на
отрезке [1;
1], принимает равные значения в граничных
точках отрезка
на
отрезке [1;
1] удовлетворяет всем требованиям теоремы
Ролля. Функция является непрерывной на
отрезке [1;
1], принимает равные значения в граничных
точках отрезка
![]() и ее производная
и ее производная
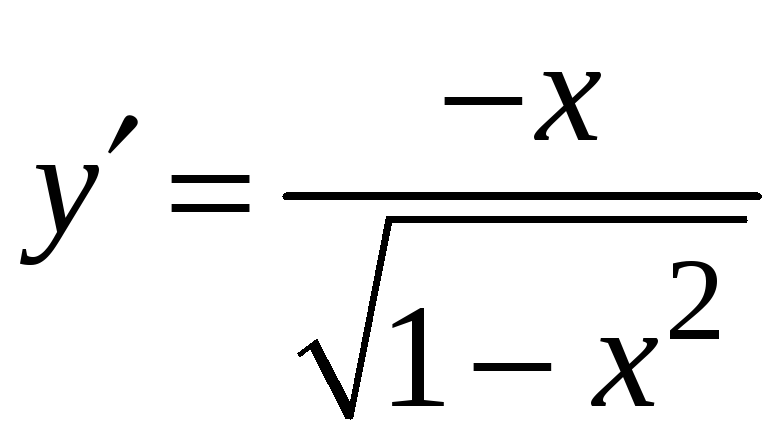 существует в каждой внутренней точке
отрезка. В граничных точках отрезка
производная не существует (бесконечная).
В теореме Ролля не требуется
дифференцируемости функции в граничных
точках отрезка. Всего этого достаточно,
чтобы существовала внутренняя точка
отрезка х
= 0, в которой производная равна нулю, а
касательная параллельна оси Ох
(рис. 26).
существует в каждой внутренней точке
отрезка. В граничных точках отрезка
производная не существует (бесконечная).
В теореме Ролля не требуется
дифференцируемости функции в граничных
точках отрезка. Всего этого достаточно,
чтобы существовала внутренняя точка
отрезка х
= 0, в которой производная равна нулю, а
касательная параллельна оси Ох
(рис. 26).