2.4.4. Применение формулы Маклорена для вычисления пределов и значений функций
Пример 2.18.
Найти предел
.
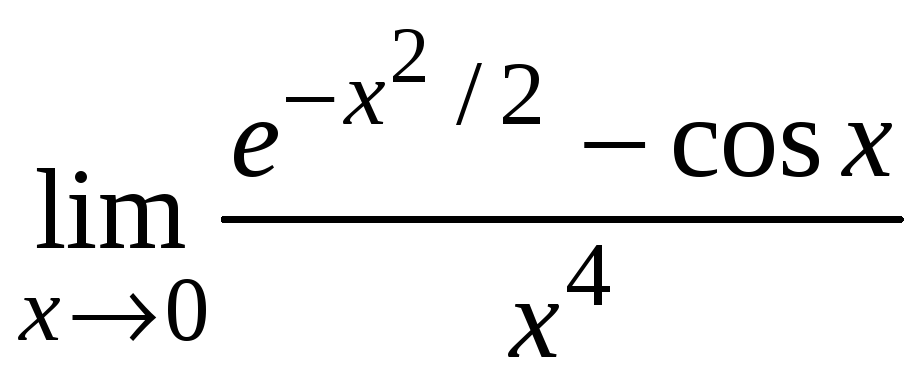Используя формулу
Маклорена, разложим по степеням х
функции
и cosx.
В разложениях возьмем столько слагаемых,
чтобы остаточные члены (они записаны в
форме Пеано) были более высокого порядка
малости, чем бесконечно малая функция
,
стоящая в знаменателе. Выполним приведение
подобных. Учтем, что сумма (разность)
бесконечно малых функций
и
является
.
Получим
.
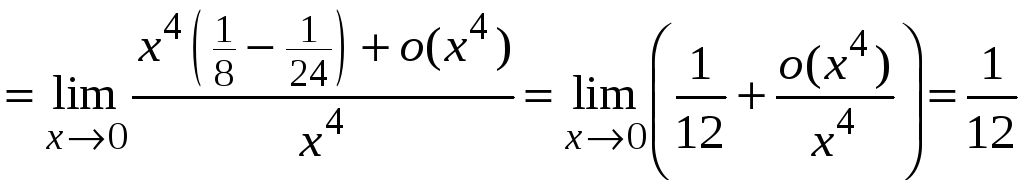Пример 2.19.
.
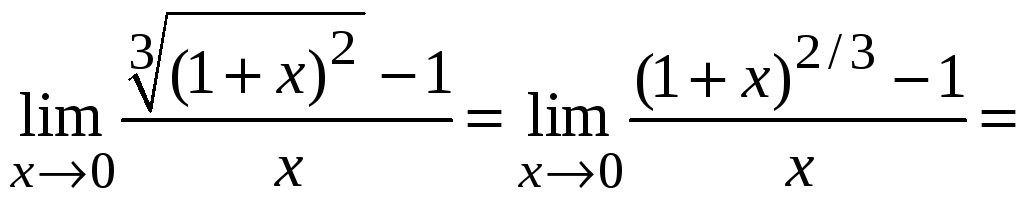
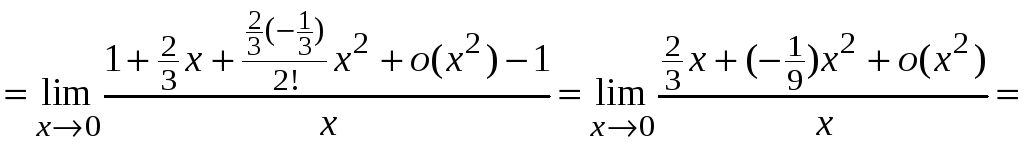
Пример 2.20.
Вычислить
число е
с точностью
.
Запишем разложение
функции
по
степеням х
,
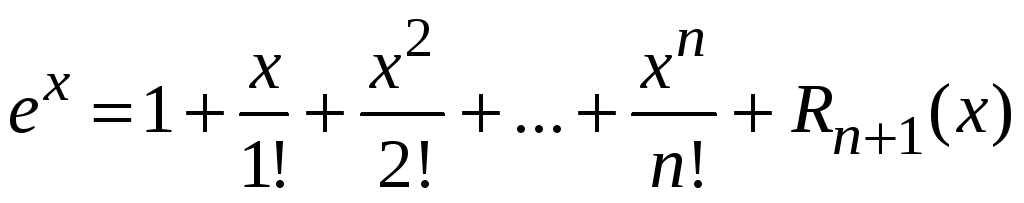где
,
.
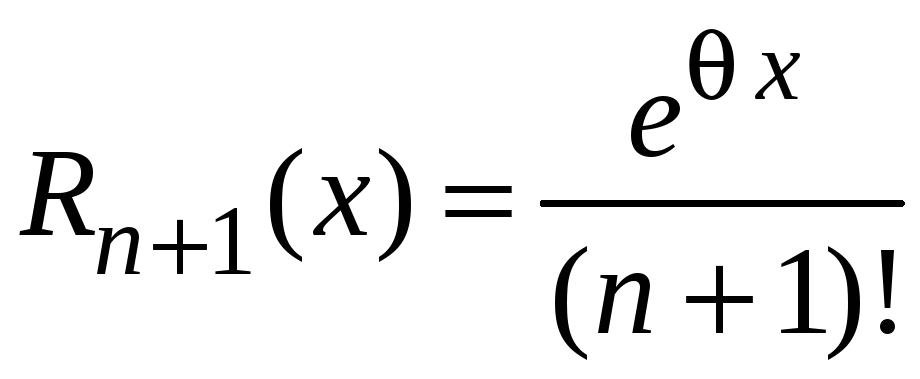При х
= 1 получим
.
Пусть нам известно,
что это число меньше трех (e
<3), поэтому можно записать
.
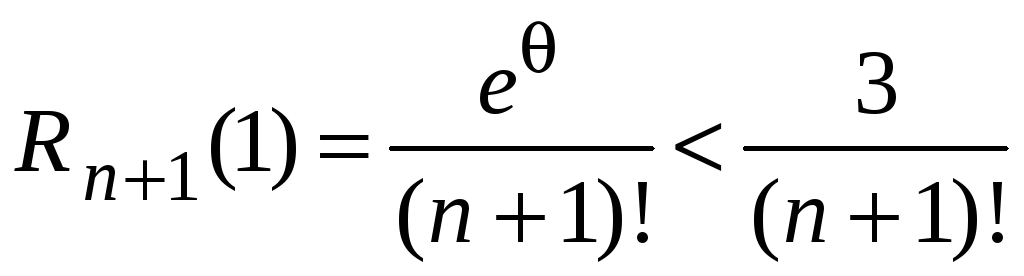Найдем оценку остаточного члена при
различных значениях n,
равных 1, 2, 3, 4, 5, 6. Получим
n
= 1,
;
n
= 2,
;
n
= 3,
;
n
= 4,
;
n
= 5,
;
n
= 6,
.
Следовательно,
для того, чтобы вычислить значение числа
е
с точностью
,
необходимо учесть в разложении по
формуле Маклорена 6 слагаемых. Находим
.
2.5. Исследование функций
2.5.1. Необходимый и достаточный признаки монотонности функций
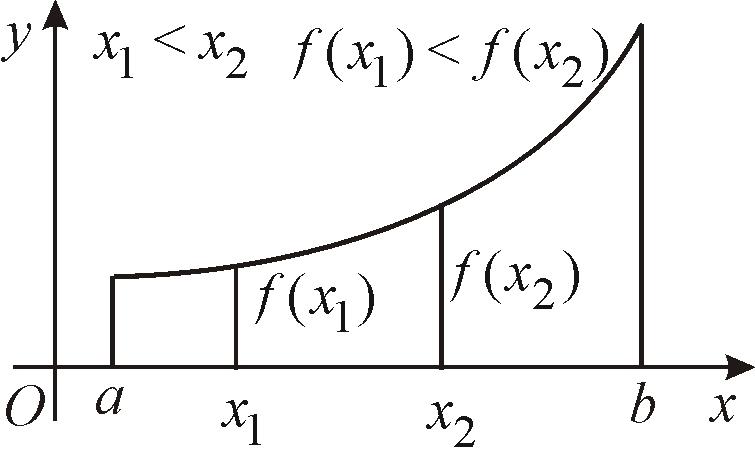
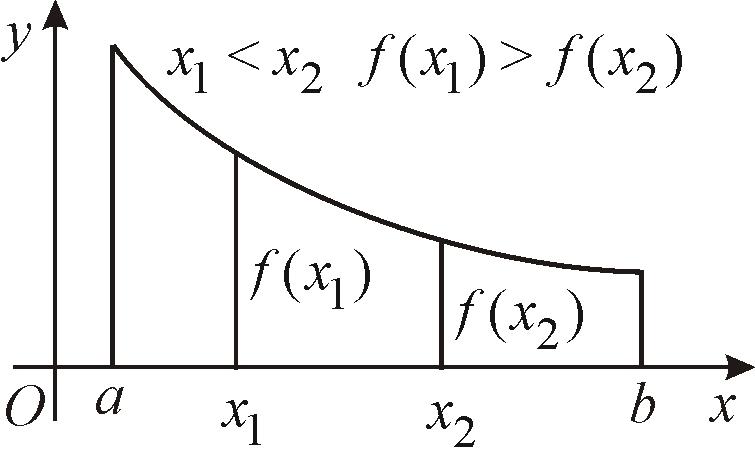
Функция называется
монотонно возрастающей (рис.29) (убывающей
(рис.30)) на интервале (a,
b),
если
,
(
).
|
Рис. 29 |
Рис. 30 |
Теорема
2.3. Необходимый
признак монотонности функции. Если
функция
монотонно возрастает (убывает) на
интервале (a,
b),
то ее производная в любой точке этого
интервала неотрицательная (неположительная).
Д о к а з а т е л ь
с т в о. Пусть функция
монотонно возрастает на интервале (a,
b).
Тогда для любого
и
.
Аналогично для монотонно убывающей
функции. Если
и
.
Теорема
2.4. Достаточный
признак монотонности функции. Если на
интервале (a,
b)
для любого значения х
производная функции положительная
(отрицательная
),
то функция монотонно возрастает
(убывает).
Д о к а з а т е л ь
с т в о. Пусть
.
Пусть точки
произвольно выбранные на интервале
(a,
b)
и
.
На отрезке
функция
удовлетворяет условиям теоремы Лагранжа,
согласно которой
,
где
.
По предположению
,
,
поэтому
,
т. е. функция
является возрастающей. Аналогично можно
показать, что при
функция
является убывающей.
2.5.2. Определение экстремума функции
|
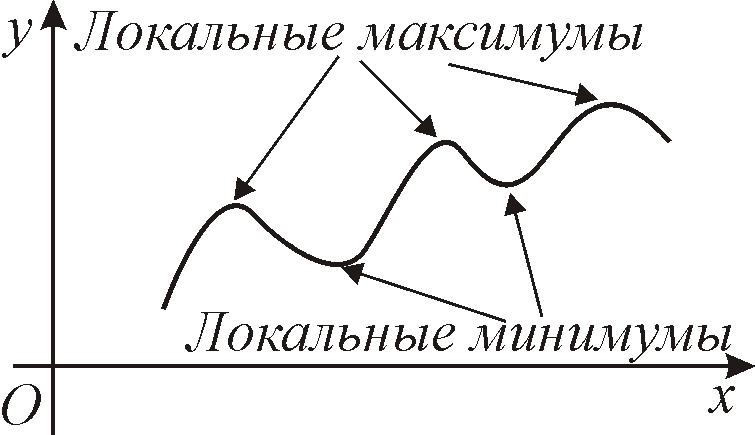
Рис. 31 |
Точка
|
называется точкой локального максимума
(минимума) функции
,
если существует некоторая окрестность
этой точки
,
что для любой точки этой окрестности
(
)
(Рис. 31).Максимум и минимум функции называются экстремумами.
2.5.3. Необходимый признак экстремума функции
Теорема
2.5. Если точка
является точкой экстремума функции
,
то производная функции в этой точке
либо равна нулю, либо не существует.
Д ок а з а т е л ь с т в о. Рассмотрим два возможных случая.
1. Пусть функция
является дифференцируемой на некотором
интервале (a,
b).
Тогда функция является непрерывной и
имеет конечные производные в любой
точке (a,
b).
Пусть
является точкой максимума. Тогда
существует такая -окрестность
этой точки
,
что для любого приращения независимой
переменной, положительного х
>
0 или отрицательного х
< 0, приращение
функции
.
Найдем односторонние пределы в точке
.
,
.
Необходимым и
достаточным условием существования
предела в точке является существование
односторонних пределов и равенство их
между собой
.
Функция
дифференцируемая, поэтому ее производная
в точке
существует и, следовательно, равна нулю
.
2. Пусть функция
в точке
имеет экстремум и не является
дифференцируемой. Тогда ее производная
в этой точке либо неограниченна и
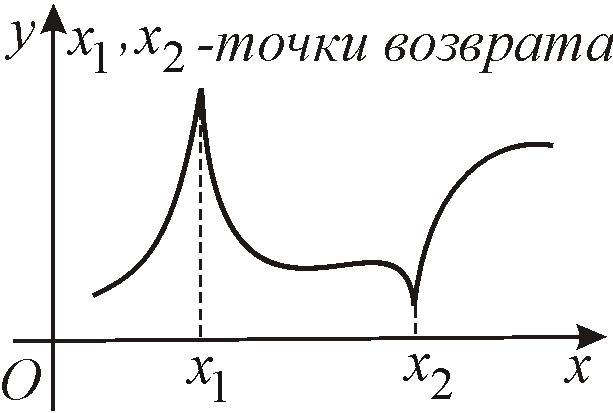
является точкой возврата (рис. 32), либо
существуют в этой точке только
односторонние производные не равные
между собой и точка является точкой
излома (рис. 33).
|
Рис. 32 |
Рис. 33 |
Точка
называется критической для функции
,
если производная функции в этой точке
либо равна нулю, либо не существует.
Таким образом,
если
точка экстремума функции, то она является
критической.