2.3.8. Применение правила Лопиталя для раскрытия неопределенностей типа степени

Если при нахождении пределов имеет место неопределенность типа степени вида , то ее необходимо привести к неопределенности типа частного. Пусть имеет место неопределенность типа степени при нахождении предела . Используем определение логарифма, преобразуем данный предел

.

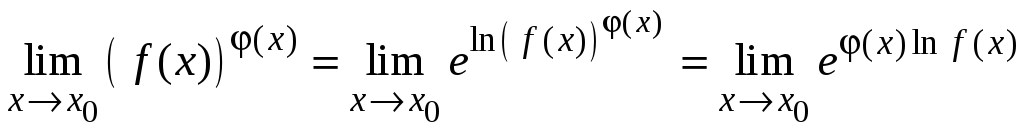Так как показательная функция является непрерывной, то можно перейти к пределу в показателе степени, т. е.

.

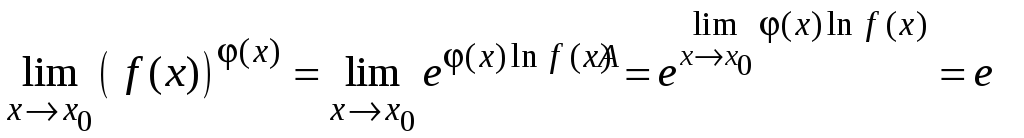При нахождении предела неопределенность имеет тип произведения, которую необходимо свести к неопределенности типа частного.

Пример 2.16. .

. .

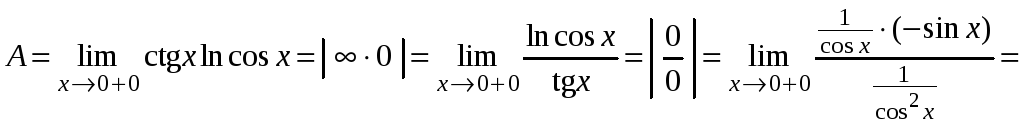
Пример 2.17. .

..

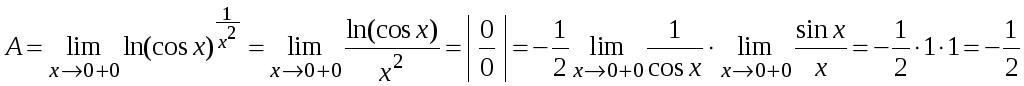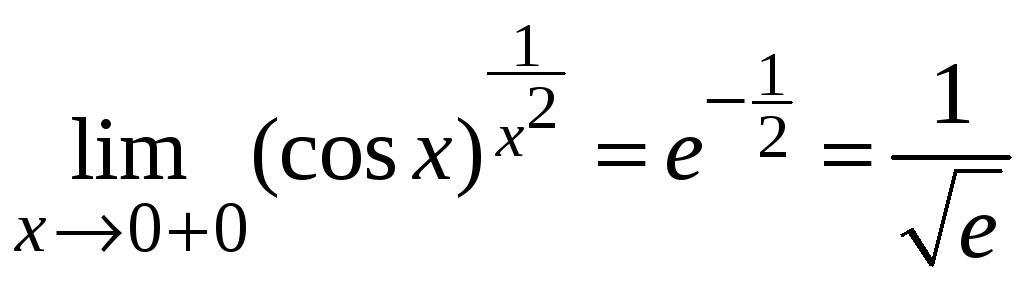2.4. Формулы Тейлора и Маклорена

2.4.1. Формула Тейлора. Остаточный член в форме Лагранжа

Теорема 2.2. Если в некоторой окрестности точки х = а функция имеет конечные производные до (n+1)-го порядка включительно, то для любой точки этой окрестности справедлива формула

,

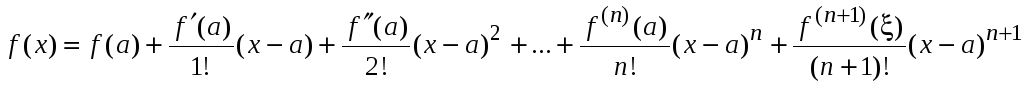где .

Д о к а з а т е л ь с т в о. Используем теорему Ролля.

Обозначим .

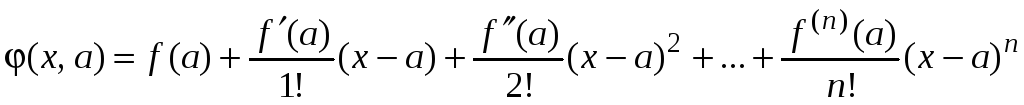Покажем, что разность , где .

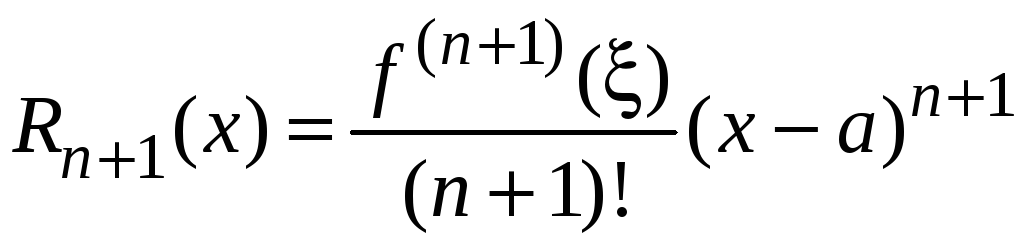Для этого составим вспомогательную функцию

.

Запишем ее подробнее

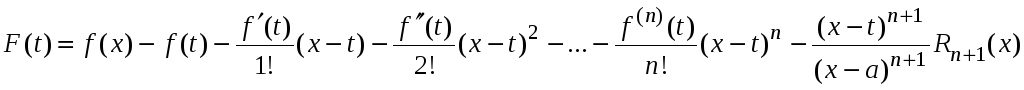и покажем, что она удовлетворяет условиям теоремы Ролля.

Очевидно, функция является непрерывной на отрезке и дифференцируемая в каждой его внутренней точке, т.е. на интервале, так как образована с помощью алгебраических действий сложения, умножения и возведение в целую степень над непрерывными и дифференцируемыми функциями. Найдем значения функции в граничных точках отрезка .

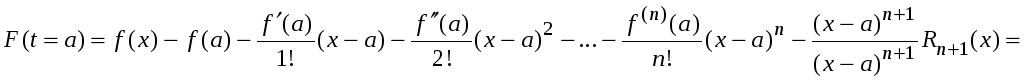
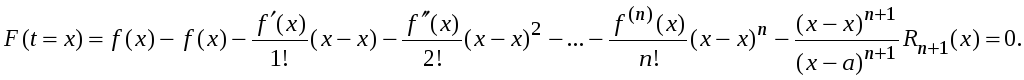. Согласно теореме Ролля существует такая точка , что . Найдем

.

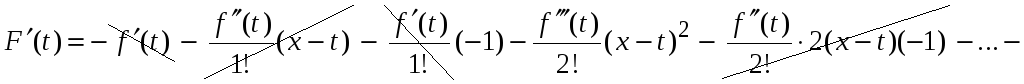
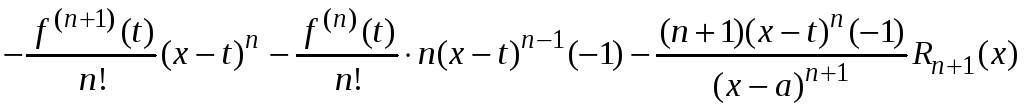Здесь в производной уничтожаются все слагаемые, первое и третье, второе и пятое и т. д., кроме двух. Имеем

.

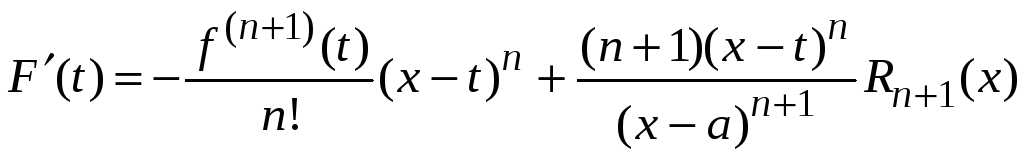Найдем значение производной в точке t = 

.

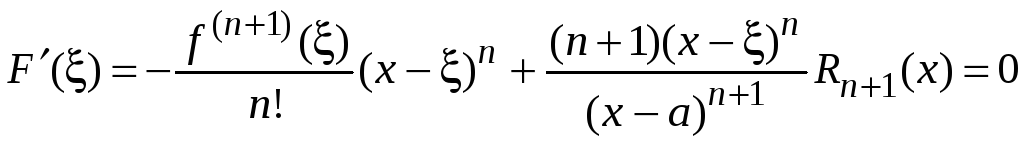Отсюда получаем

.

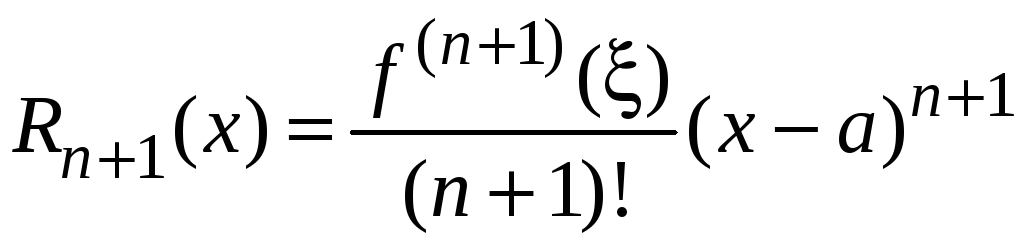Данное выражение для называется остаточным членом в форме Лагранжа.

Если представить  в виде , где , то остаточный член примет вид

.

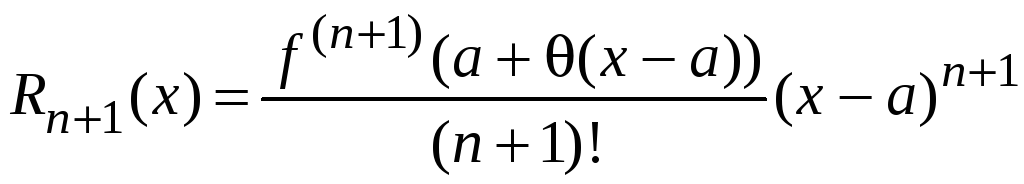В частном случае, если , , то формула Тейлора примет вид

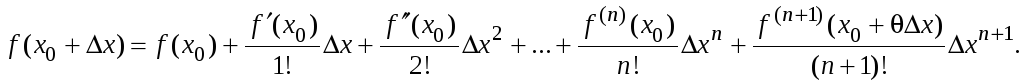При n = 0 из формулы Тейлора получается формула теоремы Лагранжа о конечном приращении функции

Найдем ,

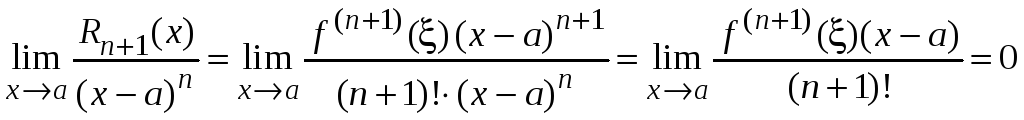т. е. остаточный член является бесконечно малой функцией по сравнению с . Поэтому его можно кратко записать следующим образом

.

Данная запись остаточного члена называется в форме Пеано.

Формула Тейлора позволяет записать функцию в окрестности некоторой точки в виде многочлена по степеням . В практических задачах часто требуется записать это разложение по степеням х, т. е. в окрестности точки х = 0.

2.4.2. Формула Маклорена

Если а = 0, то формула Тейлора принимает вид

,

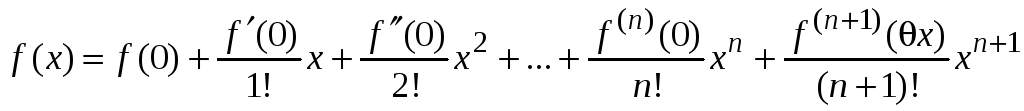где .

Данный вид формулы называется формулой Маклорена. В этом случае остаточный член (последнее слагаемое в формуле) в форме Лагранжа имеет вид 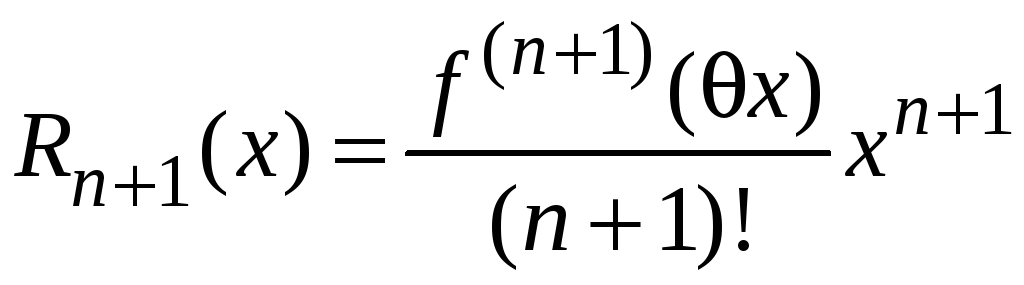, а в форме Пеано .

2.4.3. Разложение основных элементарных функций по формуле Маклорена

Найдем производные функций и их значения в начале координат (при х = 0), запишем разложения следующих функций: .

1. .

.

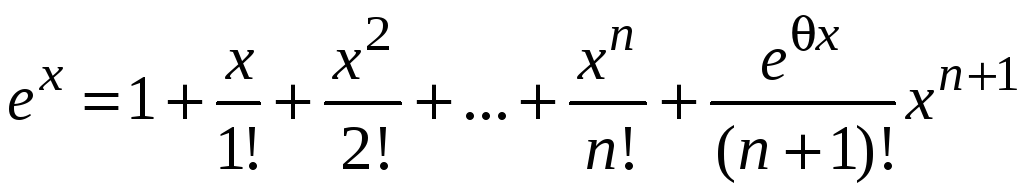2.
.
3.
.
4.						.
	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .				. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
.
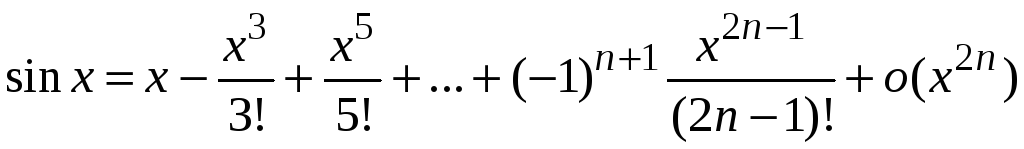