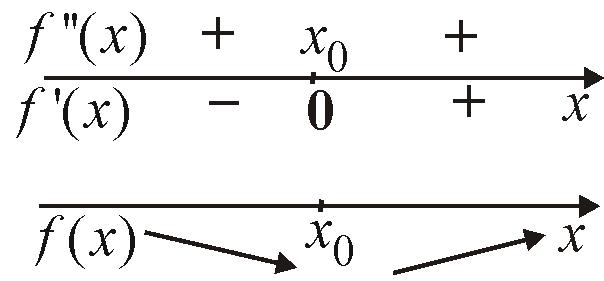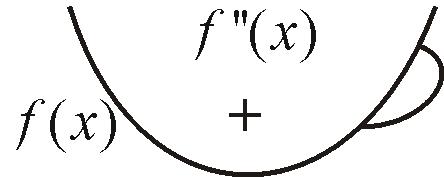- •Глава II. Дифференциальное исчисление функций одной переменной
- •2.1. Производная функции
- •2.1.1. Определение производной функции
- •2.1.2. Дифференцируемость функции, ее взаимосвязь с производной и непрерывностью функции
- •2.1.3. Непосредственное нахождение производной
- •2.1.4. Геометрический смысл производной
- •2.1.5. Механический смысл производной
- •2.1.6. Правила дифференцирования функций
- •2.1.7. Вывод производных основных элементарных функций
- •2.1.8. Сводка формул Правила дифференцирования
- •2.1.9. Производные высших порядков
- •2.1.10. Эластичность функции
- •2.1.11. Геометрический смысл эластичности
- •2.1.12. Экономический смысл эластичности
- •2.1.13. Свойства эластичности функции
- •2.2. Дифференциал функции одной переменной
- •2.2.1. Определение дифференциала функции
- •2.2.2. Геометрический смысл дифференциала
- •2.2.3. Свойства дифференциала
- •2.2.4. Применение дифференциала для приближенных вычислений
- •2.2.5. Дифференциалы высших порядков
- •2.3. Теоремы о дифференцируемых функциях
- •2.3.1. Теорема Ролля
- •2.3.2. Геометрический смысл теоремы Ролля
- •2.3.3. Примеры использования теоремы Ролля
- •2.3.4. Теорема Лагранжа о конечном приращении функции
- •2.3.5. Геометрический смысл теоремы Лагранжа
- •2.3.6. Теорема Коши
- •2.3.7. Раскрытие неопределенностей при нахождении пределов. Правило Лопиталя
- •2.3.8. Применение правила Лопиталя для раскрытия неопределенностей типа степени
- •2.4. Формулы Тейлора и Маклорена
- •2.4.1. Формула Тейлора. Остаточный член в форме Лагранжа
- •2.4.2. Формула Маклорена
- •2.4.3. Разложение основных элементарных функций по формуле Маклорена
- •2.4.4. Применение формулы Маклорена для вычисления пределов и значений функций
- •2.5. Исследование функций
- •2.5.1. Необходимый и достаточный признаки монотонности функций
- •2.5.2. Определение экстремума функции
- •2.5.3. Необходимый признак экстремума функции
- •2.5.4. Первый достаточный признак экстремума функции (с использованием первой производной)
- •2.5.5. Второй достаточный признак экстремума функции (с использованием производной второго порядка)
- •2.5.6. Определение выпуклости, вогнутости графика функции, точки перегиба
- •2.5.7. Достаточный признак выпуклости, вогнутости графика функции
- •2.5.8. Необходимый признак существования точки перегиба
- •2.5.9. Достаточный признак существования точки перегиба
- •2.5.10. Асимптоты графика функции
- •2.5.11. Построение графика функции
2.5.4. Первый достаточный признак экстремума функции (с использованием первой производной)
Теорема
2.6. Если в
окрестности критической точки
![]() функция
функция
![]() является непрерывной, а так же
дифференцируемой в этой окрестности,
за исключением быть может самой точки,
и при переходе х
через
является непрерывной, а так же
дифференцируемой в этой окрестности,
за исключением быть может самой точки,
и при переходе х
через
![]() производная
производная
![]() изменяет знак, то
изменяет знак, то
![]() является точкой локального экстремума;
причем, если знак
является точкой локального экстремума;
причем, если знак
![]() изменяется с «+» на «»,
то
изменяется с «+» на «»,
то
![]()
точка максимума, если знак изменяется
с «»
на «+», то
точка максимума, если знак изменяется
с «»
на «+», то
![]()
точка минимума.
точка минимума.
Д о к а з а т е л ь
с т в о. Пусть в -окрестности
критической точки
![]() знак
знак
![]() изменяется с «+» на «».
Тогда по достаточному признаку
монотонности функции на интервале
изменяется с «+» на «».
Тогда по достаточному признаку
монотонности функции на интервале
![]() функция возрастает, а на интервале
функция возрастает, а на интервале
![]() функция убывает, т. е.
функция убывает, т. е.
![]() является точкой локального максимума.
Аналогично для случая изменения знака
производной функции с «»
на «+», функция на интервале
является точкой локального максимума.
Аналогично для случая изменения знака
производной функции с «»
на «+», функция на интервале
![]() убывает, а на интервале
убывает, а на интервале
![]() возрастает и точка
возрастает и точка
![]() является точкой минимума.
является точкой минимума.
2.5.5. Второй достаточный признак экстремума функции (с использованием производной второго порядка)
Теорема
2.7. Если
функция
![]() является непрерывной и дважды
дифференцируемой в окрестности точки
является непрерывной и дважды
дифференцируемой в окрестности точки
![]() ,
производная функции в этой точке равна
нулю
,
производная функции в этой точке равна
нулю
![]() ,
а производная второго порядка отлична
от нуля
,
а производная второго порядка отлична
от нуля
![]() ,
то
,
то
![]() является точкой локального экстремума
функции; причем, если
является точкой локального экстремума
функции; причем, если
![]() ,
то имеет место минимум, а если
,
то имеет место минимум, а если
![]()
максимум.
максимум.
Д о к а з а т е л ь
с т в о. Пусть в точке
![]()
![]() ,
,
![]() (рис.34).
(рис.34).
Так как
![]() является производной от производной
является производной от производной
![]() ,
то она определяет характер изменения
функции
,
то она определяет характер изменения
функции
![]() .
По предположению
.
По предположению
![]() .
Так как
.
Так как
![]() непрерывная функция, то она больше
нуля не только в точке
непрерывная функция, то она больше
нуля не только в точке
![]() ,
но и в некоторой окрестности этой точки
,
но и в некоторой окрестности этой точки
![]() .
.
|
Рис. 34 |
Так как
|
По первому
достаточному признаку экстремума в
этом случае в точке
![]() имеет место минимум.
имеет место минимум.
Аналогично можно
показать, что если
![]() ,
то
,
то
![]() является точкой максимума.
является точкой максимума.
Пример
2.21. Исследовать
на экстремум функцию
![]() .
.
|
Рис.35 |
Найдем
|
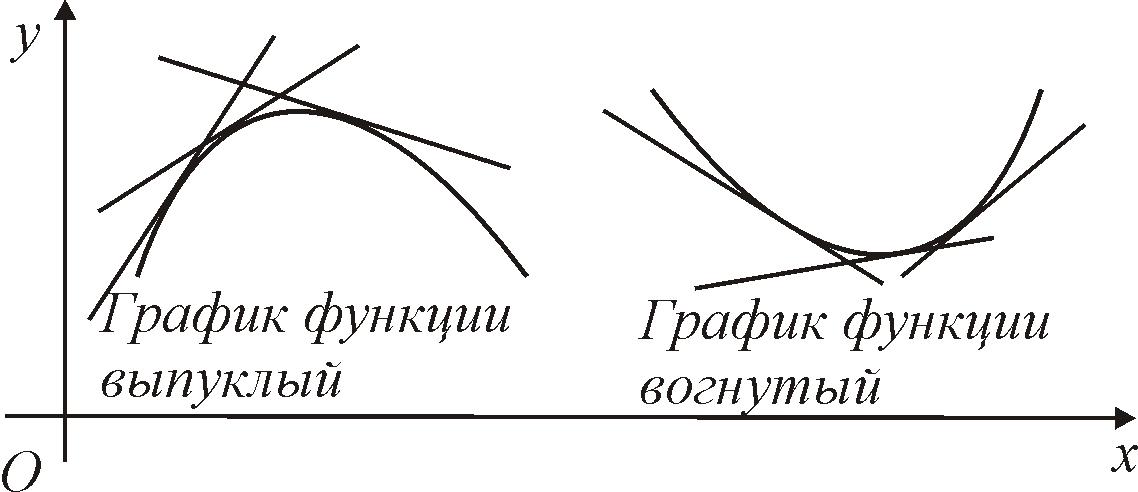
2.5.6. Определение выпуклости, вогнутости графика функции, точки перегиба
|
Рис. 36 |
График функции называется выпуклым (вогнутым) вверх на некотором интервале, если он находится ниже (выше) касательной к графику функции, проведенной в любой точке этого интервала (рис. 36). |
2.5.7. Достаточный признак выпуклости, вогнутости графика функции
Теорема
2.8. Если
функция
![]() является непрерывной и дважды
дифференцируемой на интервале
является непрерывной и дважды
дифференцируемой на интервале
![]() и производная второго порядка в любой
точке этого интервала положительная
и производная второго порядка в любой
точке этого интервала положительная
![]() (отрицательная
(отрицательная
![]() ),
то график функции является вогнутым
(выпуклым)
),
то график функции является вогнутым
(выпуклым)
на этом интервале.
Д о к а з а т е л ь
с т в о. Пусть
![]() касательная к графику функции
касательная к графику функции
![]() ,
проведенная в произвольно выбранной
на интервале
,
проведенная в произвольно выбранной
на интервале
![]() точке
точке
![]() (рис. 37).
(рис. 37).
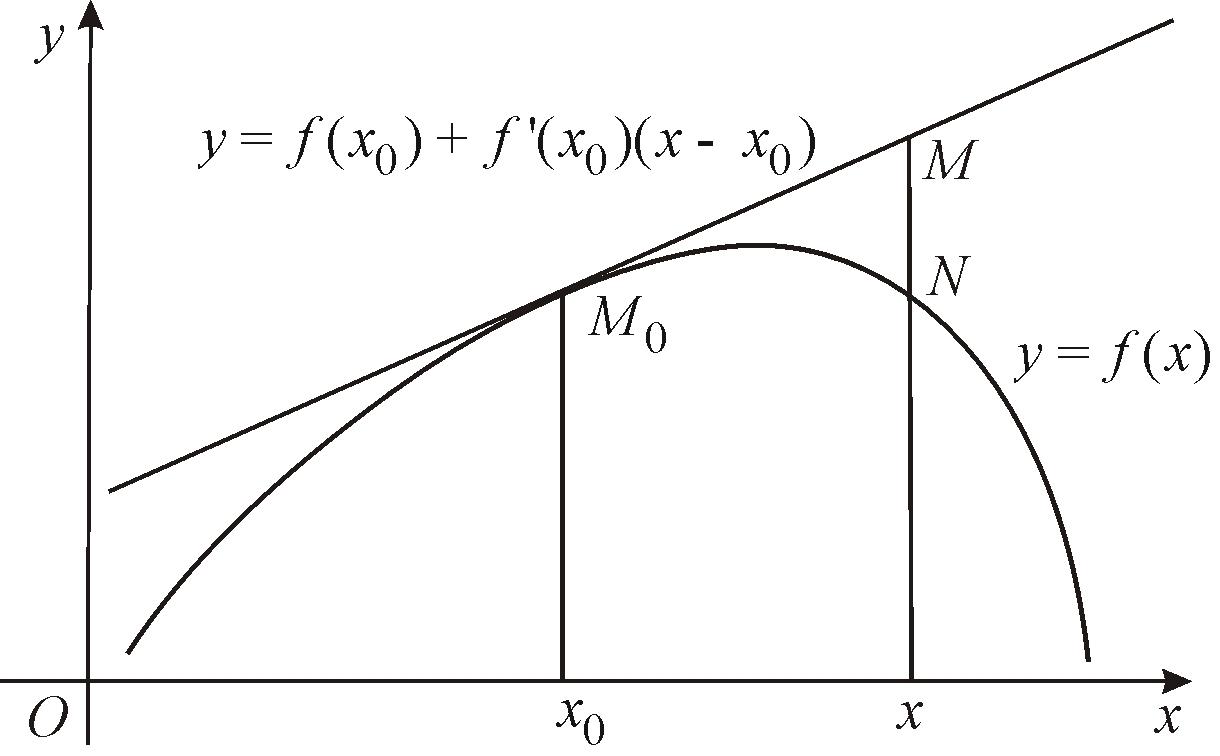
Рис. 37
О
характере выпуклости (вогнутости)
графика функции будем судить по разности
MN
ординат графиков функции
![]() и касательной
и касательной
![]() в точке х.
Используем разложение функции
в точке х.
Используем разложение функции
![]() в окрестности точки
в окрестности точки
![]() по формуле Тейлора (достаточно учесть
два слагаемых и остаточный член)
по формуле Тейлора (достаточно учесть
два слагаемых и остаточный член)
![]() ,
где
,
где
![]() .
.
Запишем

![]() .
.
Отсюда следует,
что если
![]() ,
то MN
> 0 и на
интервале
,
то MN
> 0 и на
интервале
![]() график вогнутый. Если же
график вогнутый. Если же
![]() ,
то MN
< 0 и график
функции выпуклый.
,
то MN
< 0 и график
функции выпуклый.
Запоминают
следующим образом. Если
![]() («+»), то график функции вогнутый (вода
производная второго порядка держится
на кривой) (рис. 37а). Если
(«+»), то график функции вогнутый (вода
производная второго порядка держится
на кривой) (рис. 37а). Если
![]() («»),
то график функции выпуклый (вода
производная второго порядка скатывается
с кривой) (рис. 37а).
(«»),
то график функции выпуклый (вода
производная второго порядка скатывается
с кривой) (рис. 37а).
|
Рис. 37а |
Рис. 37б |