
- •Физические основы механики.
- •1. Кинематика поступательного движения.
- •1.1 Механическое движение.
- •1.2.Пространство и время.
- •1.3. Система отсчета.
- •1.4. Кинематические уравнения движения.
- •1.5. Перемещение, элементарное перемещение.
- •1.6. Скорость.
- •1.7. Ускорение. Нормальное и тангенциальное ускорения.
- •2.Динамика поступательного движения
- •2.1. Поступательное движение
- •2.2. Закон инерции.
- •2.3. Инерциальная система отсчета.
- •2.4. Масса. Второй закон Ньютона.
- •2.5. Сила.
- •2.6.Основной закон динамики материальной точки.
- •2.7. Третий закон Ньютона
- •2.8. Преобразования Галилея
- •Продифференцировав их по времени, получим связь между скоростями точки а в системах отсчета и в векторной и координатной формах:
- •2.9. Принцип относительности Галилея
- •Законы сохранения.
- •Сохраняющиеся величины
- •3.3 Центр масс
- •3.4. Уравнение движения центра масс.
- •4.Работа и энергия
- •4.1 Работа
- •2. Работа упругой силы
- •4.3. Консервативные силы
- •4.4. Центральные силы.
- •4.5. Потенциальная энергия частицы в силовом поле.
- •4.6. Связь между потенциальной энергией и силой для консервативного поля.
- •4.7. Кинетическая энергия частицы в силовом поле.
- •4.8. Полная механическая энергия частицы.
- •4.9. Закон сохранения механической энергии частицы.
- •5.Кинематика и динамика вращательного движения.
- •5.1.Кинематика.
- •5.2. Момент импульса частицы. Момент силы.
- •5.3. Момент импульса и момент силы относительно оси.
- •5.4. Закон сохранения момента импульса системы.
- •5.5. Момент инерции твердого тела.
- •5.6. Уравнение динамики вращения твердого тела.
- •5.7. Кинетическая энергия вращающегося тела.
- •5.8. Работа вращения твердого тела.
- •6.Неинерциальные системы отсчёта
- •6.1 Силы инерции (Сав. Стр.118)
- •6.2. Центробежная сила инерции
- •6.3 Сила Кориолиса
- •7.Механические колебания
- •7.1 Общие сведения
- •7.1 Малые колебания
- •7.2 Гармонические колебания.
- •7.3 Математический маятник Это материальная точка, подвешенная на нерастяжимой нити длиною , совершающая колебания в вертикальной плоскости под действием силы тяжести.
- •Записав для пути точки: , а для ускорения , запишем уравнение движения вдоль оси : . Или для малых углов (когда )
- •7.4. Физический маятник.
- •7.5 Затухающие колебания
- •7.6 Автоколебания
- •7.7 Вынужденные колебания
- •7.8 Резонанс
- •8. Волны
- •8.1 Распространение волн в упругой среде.
- •8.2 Уравнение плоской и сферической волн.
- •8.3. Волновое уравнение
- •Подставим в уравнение () и и учтем, что , получим:
8.3. Волновое уравнение
Уравнение волны является решением дифференциального уравнения, называемого волновым.
Для
его установления найдем вторые частные
производные по времени и координатам
от уравнения волны.
![]() (1)
(1)
![]() (2),
известно, что
(2),
известно, что
![]()
Аналогичные
уравнения (3) и (4) можно записать для
координат
![]() и
и
![]() .
.
Сложив производные по координатам, получим:
![]() (5)
(5)
Величина
![]() обозначается знаком
обозначается знаком
![]() и называется оператором Лапласа
(лапласиан). Сопоставив уравнения (1) и
(5), получим :
и называется оператором Лапласа
(лапласиан). Сопоставив уравнения (1) и
(5), получим :
![]() или
или
![]()
![]() (6)
– волновое
уравнение.
(6)
– волновое
уравнение.
Любая
функция, удовлетворяющая уравнению
(6), описывает некоторую волну, при этом
корень квадратный из величины обратной
коэффициенту при второй производной
по времени дает фазовую скорость волны.![]()
8.4 Энергия волны.
Упругая среда, в которой распространяются механические волны, обладает как кинетической энергией колебательного движения частиц, так и потенциальной энергией, обусловленной деформацией среды при движении волны.
Кинетическая
энергия малого объема
![]() среды
с плотностью
среды
с плотностью
![]() ,
в котором все частицы движутся с
одинаковой скоростью
,
в котором все частицы движутся с
одинаковой скоростью
![]() равна:
равна:
![]() ,
а объемная плотность энергии
,
а объемная плотность энергии
![]() .
.
Потенциальная энергия малого объема упруго – деформированной среды:
![]() ,
где
,
где
![]() - фазовая скорость волны в среде,
- фазовая скорость волны в среде,
![]() -
относительная деформация среды. Объемная
плотность потенциальной энергии:
-
относительная деформация среды. Объемная
плотность потенциальной энергии:
![]()
Сумма
дает объемную плотность энергии упругих
волн, т.е., объемную плотность механической
энергии среды, обусловленную
распространением волн, равную:![]()
![]() ()
для определенной координаты и времени.
()
для определенной координаты и времени.
Если
в среде распространяется продольная
плоская волна вдоль оси
![]() ,
,
![]() ,
то скорость колебаний частиц малого
объема:
,
то скорость колебаний частиц малого
объема:
![]() .
А деформация этого объема:
.
А деформация этого объема:
![]() .
.
Подставим в уравнение () и и учтем, что , получим:
![]() -
плоская волна.
-
плоская волна.
Таким
образом, объемная плотность энегрии
волны зависит как от координаты, так и
от времени. В каждый момент времени она
разная в разных точках среды. В одной и
той же точке она изменяется со временем
по закону
![]() .
Т.к., среднее значение
.
Т.к., среднее значение
![]() равно ½, то среднее по времени значение
энергии в каждой точке среды:
равно ½, то среднее по времени значение
энергии в каждой точке среды:
![]()
т.е., пропорционально плотности среды, квадрату амплитуды и частоты.

Рис.8,3 а)
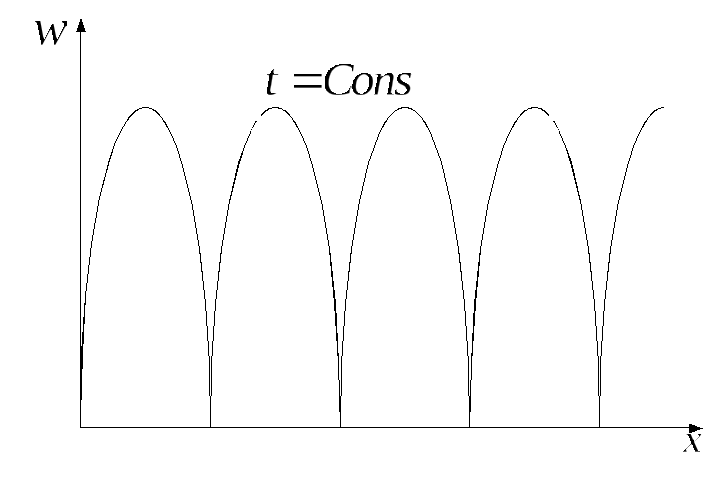
Рис.8,3б
