Динамика вязкого газа, турбулентность и струи

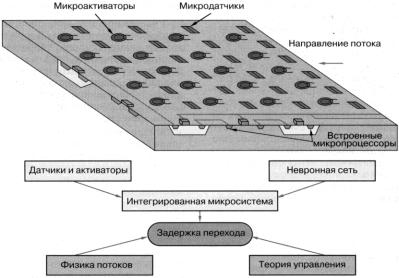
11.2. Активное управление пограничным слоем

121

В существующих методах управления невозможно идентифицировать структуры и провести выборочное управление ими в реальном времени.

Совсем недавно появилось новое направление в технике. Грандиозные достижения в микроэлектронике были применены для создания микромашин. Новейшие технологии позволяют производить механические части и целые устройства микронных размеров (рис. 11.8) для применения в различных областях техники. Для механики жидкости и газа эта технология дает возможность создавать микродатчики и микроустройства для управления течением. Их масса, теплопроводность и другие инерциальные характеристики очень малы. Таким образом, удовлетворяется основное требование к датчикам и активаторам – отклик на высокие частоты. Более того, можно достичь интерактивного распределенного управления соединением на одной поверхности микродатчиков, микроактиваторов и микропроцессоров для создания интегрированной системы.

Рис. 11.8

Рис.34.

Такая система имеет на поверхности датчики напряжения сдвига, улавливающие локализованные вихри возмущений в нелинейной области пограничного слоя, встроенную сеть для обработки сигналов в соответствии с алгоритмом распознавания образов и набор магнитных закрылков для управления вихрями. Этот подход может открыть новые горизонты для интерактивного управления течениями, но также ставит новые научные и инженерные задачи:

122	11. МЕТОДЫ УПРАВЛЕНИЯ ПОГРАНИЧНЫМ СЛОЕМ

построение распределенного управления, исследование усталостных свойств микромеханических частей и изучение течений сплошной среды на микронном уровне. В то же время набор микроактиваторов способен контролировать макрообъект при условии существования подходящего механизма управления. Например, можно использовать линейный набор выдвижных линейных активаторов для создания вращающего момента на модели дельтовидного крыла.

Таким образом, теория гидродинамической устойчивости и экспериментальное моделирование в настоящее время являются мощными средствами в исследовании динамики жидкости и газа. Они позволяют исследовать наиболее сложные явления ламинарно-турбулентного перехода и дают основу для современных стратегий управления переходом.

До сих пор способы управления пограничными слоями были сконцентрированы на пассивных подходах. Устройствами такого типа можно было пытаться подавить формирование или взаимодействие организованных структур в течении. Эти устройства играют пассивную роль в том смысле, что не существует цепи обратной связи для детектирования структур в течении и манипулирования ими. Современные работы направлены на активное управление динамическими структурами для достижения задержки перехода или уменьшения поверхностного трения. Стратегия управления реализуется через цепь обратной связи при изменении структур в потоке.

Микроэлектромеханические системы имеют дело с явлениями в специфическом микронном масштабе расстояний. Многие интересные научные проблемы необходимо понять в микромеханике сплошных сред. В частности, управляющие механизмы меняются и многие фундаментальные знания оказываются под вопросом. Наиболее интересно то, что мы сможем осуществлять интерактивное управление в реальном времени фактически случайными событиями и эксплуатировать явления вне пределов разрешения традиционных устройств.

12.ТУРБУЛЕНТНЫЕ ТЕЧЕНИЯ

Турбулентные течения наиболее распространены в природе и очень усложняют все задачи, встречающиеся в динамике вязкого

газа. Возникновение турбулентного режима течения приводит к увеличению аэродинамического сопротивления, более интенсивному нагреву поверхности летательных аппаратов, затягиванию отрыва потока. Для турбулентных течений характерны чрезвычайно нерегулярные, беспорядочные изменения параметров течения со временем в каждой точке пространства (развитая турбулентность) и такие же нерегулярные изменения от точки к точке потока.

По мере увеличения числа Рейнольдса в потоке появляются сначала крупномасштабные пульсации. При больших значениях Re в потоке присутствуют пульсации самого разного масштаба. Наибольшим характерным размером является толщина пограничного слоя . Наименьшим масштабом, на котором происходит постоянный переход энергии от крупномасштабных пульсаций через мелкомасштабные в тепло (обнаружил L. Richardson, 1922) является

ж		ц1/4
колмогоровский масштаб = з		ч	. Здесь – скорость диссипации энергии
и		ш

турбулентности. Для поддержания стационарного состояния потока необходимо наличие внешних источников энергии, непрерывно передающих ее основному крупномасштабному движению.

Численное моделирование турбулентных течений представляет сложную математическую задачу. Самым общим подходом к турбулентности было бы прямое численное моделирование уравнений Навье–Стокса. Однако в реаль-

ных течениях отношение масштабов /	~ 103 и расчетная сетка для численно-
го моделирования должна содержать ( /	)3 ~ 109 узлов в объеме ~ 3, что в на-

стоящее время совершенно нереально. Для описания турбулентных течений, как правило, используются упрощающие модели, основанные на усреднении уравнений движения.

124	12. ТУРБУЛЕНТНЫЕ ТЕЧЕНИЯ

12.1. Уравнения Рейнольдса

Введем понятие о средних значениях параметров потока, получающихся в результате усреднения по большим промежуткам времени истинных значений в каждой точке пространства. Отклонения истинных значений от средних будем называть пульсационной частью. При описании турбулентного движения мгновенная скорость и давление представляются в виде суммы составляющих для усредненного потока (V, P) и наложенных турбулентных пульсаций (vi, p). Подставим эти суммы в уравнения Навье–Стокса

й	¶	+ (V j + v j )	¶	щ	(Vi + vi ) = -			¶	(P + p) +	¶2	(Vi + vi ),
к				ъ
								¶xi		¶x2
к	¶t		¶x j ъ
л				ы						j	(12.1)
					¶		(Vi + vi ) = 0.
						¶x
						i

Поскольку ¶v j 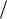¶x j = 0 , из уравнения неразрывности (12.1) после усреднения получим, что ¶V j ¶x j = 0 . Вычитание этого выражения из уравнения неразрывности дает

¶v j

¶x j

= 0 .

(12.2)

Усредняя величины в уравнении движения, получим

ж

ц

¶2V

¶V

¶V

¶P

¶v

з

i

+V j

i

ч

= -

+

i - v j

i

.

(12.3)

и

¶t

¶x j ш

¶xi

¶x2j

¶x j

Умножение уравнения неразрывности в (12.1) на (Vi + vi) и усреднение дают

v j ¶vi ¶xi = 0 . Тогда уравнение (12.3) можно переписать в виде

ж ¶V

¶V

ц

¶P

¶ ж ¶V

ц

з

i

+V

j

i

ч

= -

+

з

i

-

v v

j ч

.

(12.4)

¶t

¶xi

¶x j

i

и

¶x j ш

¶x j и

ш

Уравнения (12.4) известны как уравнения Рейнольдса.

12.2. Гипотеза Буссинеска

125

Сравнивая (12.4) с уравнениями Навье–Стокса для ламинарного потока, видим, что полное напряжение теперь определяется как

				(12.5)
ij = ij - uiv j ,
где добавочные турбулентные напряжения uiv j				получили название напряже-

ний Рейнольдса или кажущихся напряжений турбулентного течения. В общем случае они значительно превосходят напряжения, обусловленные молекулярной вязкостью жидкости.

Граничные условия для усредненных величин остаются прежними – это условия прилипания. Пульсации скорости на твердых поверхностях тоже обращаются в нуль, и поэтому исчезают добавочные турбулентные напряжения в выражении (12.5). В непосредственной близости к поверхности напряжения будут определяться только вязкими напряжениями и течение будет ламинарным. Область течения в непосредственной близости к поверхности называется ламинарным подслоем. В ламинарном подслое преобладают вязкие силы. По мере удаления от поверхности мы перейдем в переходную область, а затем – в область развитой турбулентности.

12.2. Гипотеза Буссинеска

Уравнения Рейнольдса дают возможность качественно понять структуру течения, но мало помогают количественному описанию. Для того чтобы приступить к решению уравнений, необходимо замкнуть уравнения, связать компоненты напряжений Рейнольдса со средними характеристиками течения. Задание таких связей определяет задание модели турбулентности. В разделах 12.2, 12.3 и 12.4 описаны два полуэмпирических подхода к замыканию уравнений Рейнольдса, так называемые алгебраические модели турбулентности.

Общая идея полуэмпирического подхода сформулирована Т.В. Буссинеском (T.V. Boussinesq, 1925). По аналогии с законом Стокса для ламинарных течений он предположил, что турбулентное касательное напряжение определяется формулой (так называемая градиентная гипотеза)

				= A	¶ui
	m	= - uўuў				,	(12.6)
			i j		¶x j

126						12. ТУРБУЛЕНТНЫЕ ТЕЧЕНИЯ
где uў		– турбулентные пульсации; ui – усредненная скорость; A – коэффици-
ij
ент турбулентного обмена.
Однако у гипотезы Буссинеска имеется крупный недостаток. Если для
ламинарных течений коэффициент вязкости						, по аналогии с которым введен
А, являлся физической константой течения, то в турбулентном течении коэф-
фициент А пропорционален приближенно первой степени скорости и необхо-
димо знать его связь с усредненным полем скоростей.
12.3. «Путь перемешивания» Прандтля
		Значительный	успех в	развитии идеи Буссинеска был достигнут
Л. Прандтлем (L. Prandtl, 1926). Рассмотрим плоскопараллельное течение, из-
меняющееся только в одном направлении (рис. 12.1). Пусть
			u = u(y),		v = 0,	w = 0.		(12.7)
Из касательных напряжений останется только
			m	= - uўvў = A ¶u .				(12.8)
						¶y
Прандтль предложил следующую упрощенную картину турбулентного
течения: в течении возникают некоторые жидкие объемы, которые обладают
своей скоростью и движутся на протяжении некоторого расстояния, сохраняя
x-составляющую своего импульса. Предположим, что один такой объем воз-
				ник в слое y1 – l, обладает скоростью u(y1 – l)
y		u(y1+l)		и перемещается на расстояние l в				направ-
				лении y. В новом слое он будет иметь
	u(y1)		l	меньшую скорость, чем окружающая среда.
		u(y1-l)	l	Разность скоростей будет равна
			y1
						ж ¶u	ц
					u1 = u ( y1) - u ( y1 - l) » l з		ч	. (12.9)
						и ¶y	ш y = y
		Рис. 12.1					1

12.3. «Путь перемешивания« Прандтля

127

При таком поперечном течении v

0 . Аналогичным образом

ж

¶u ц

u2 = -u ( y1) + u ( y1 + l) » l з

ч

,

(12.10)

и ¶y ш y = y

1

а v

0 .

Если подобрать величину l соответствующим образом, то разности u1 и

u2

можно принять за турбулентные пульсации, следовательно,

1

(

) = l

ж ¶u ц

.

(12.11)

uў

=

u1

+

u2

з

ч

2

и ¶y ш y = y

1

Следуя Прандтлю,

назовем l

путем перемешивания,

которому можно

дать такое физическое истолкование: путь перемешивания представляет собой то расстояние в поперечном направлении, которое пройдет жидкая частица, передвигаясь со средней скоростью своего первоначального слоя, так что разность ее скорости и скорости нового слоя будет равна усредненному значению абсолютной величины продольной пульсации турбулентного течения.

Возникновение поперечной пульсации скорости v можно представить следующим образом. Если две жидкие частицы, попавшие в слой y1, располагаются в нем друг за другом так, что позади оказывается частица, движущаяся быстрее, они столкнутся со скоростью 2u и получат боковое отклонение в обе стороны от y1. Если позади будет медленная частица, то в образующийся промежуток устремится окружающая жидкость и тоже возникнет поперечное движение. Из этих рассуждений следует, что поперечную пульсацию можно принять одного порядка с продольной:

ж

¶u ц

vў

= const

uў

= const l з

ч .

(12.12)

и ¶y ш

Вычислим величину u v . Обычно если частица придет снизу v

0 , это

приведет к уменьшению скорости

uў < 0 , если придет сверху v 0 –

то к

увеличению uў > 0 . Таким образом,

усредненное во времени значение

uiv j

отличается от нуля и притом отрицательно. Поэтому можно принять, что

u v

k

u

v

.

(12.13)

128 12. ТУРБУЛЕНТНЫЕ ТЕЧЕНИЯ

Учитывая выражения (12.11) и (12.12), получим

			2	ж du ц			2
	uўvў = -const l						.	(12.14)
				з		ч
				и dy ш

Так как l пока еще не определена, в нее можно включить const из выражения

(12.14). Тогда

m = l2 жз du цч2 . и dy ш

Правильнее придать формуле (12.15) следующий вид:

= l2 du ж du ц , m з ч

dy и dy ш

(12.15)

(12.16)

поскольку очевидно, что при изменении знака производной должен меняться знак касательного напряжения.

Формула Прандтля успешно применяется для расчета турбулентных течений. Входящая в нее неопределенная величина l является функцией координат, и в конкретных течениях для нее можно найти приемлемую аппроксимацию. Хорошие результаты дает подход Прандтля для расчетов турбулентных течений вдоль стенок и для свободной турбулентности.

12.4. Гипотеза подобия Кармана

Для расчета турбулентных течений желательно иметь правило, позволяющее определять зависимость l от координат. Попытку отыскать такое правило предпринял Т. Карман (Th. Karman, 1930). Он предложил следующую гипотезу: поля пульсационных скоростей во всех точках течения подобны.

Рассмотрим двумерное усредненное течение

u = u(y), v = 0, w = 0.

(12.17)

Введем функцию тока (x, y) такую, что

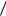u = ¶ ¶y , v = -¶ ¶x .

12.4. Гипотеза подобия Кармана

129

Дифференцируя первое уравнение движения по y, второе – по x и исключая давление, можно получить одно уравнение для , уравнение переноса вихрей,

¶

+

¶

¶

-

¶

¶

=

.

(12.18)

¶t

¶y

¶x

¶x

¶y

Пренебрежем вязкостью в уравнении (12.18)

¶

+

¶

¶

-

¶

¶

=

.

(12.19)

¶t

¶y

¶x

¶x

¶y

Пусть =

+ ў , причем ¶

¶y = u (y) № 0 . Тогда из (12.19) получим

¶ ў

ж

¶ ўц

¶

ў

¶

ў

ж d 2u

¶

ўц

+ зu

+

ч

-

з

+

ч

= 0 .

(12.20)

¶t

и

¶y ш ¶x

¶x

и dy2

¶y

ш

Разложим в ряд u в окрестности точки (x0, y0):

u u0	du	y y0	1		d 2u	y	y0	2	...
	dy		2		dy2
		0				0

Введем систему координат, движущуюся со скоростью u, и предположим, что в этой системе координат движение установившееся. Тогда приближенное уравнение (12.20) можно записать в виде

ж du ц			¶
( y - y0 )з		ч
и dy ш0			¶x

ў

ж d 2u ц

¶ ў

¶

ў ¶

ў

¶

ў ¶

ўў

= 0

. (12.21)

- з

ч

+

-

и dy2

ш

0

¶x

¶y

¶x

¶x

¶y

Исходя из гипотезы Кармана в различных точках течения подобны, т. е. различаются только масштабами длины и скорости. Пусть каждой точке течения соответствует свой масштаб длины l и свой масштаб скорости B. Введем безразмерные координаты и безразмерную функцию тока следующими выражениями:

(x– x0) = l , (y – y0) = l ,

= Blf( , ).

(12.22)

130	12. ТУРБУЛЕНТНЫЕ ТЕЧЕНИЯ

Подставив выражения (12.22) в уравнение (12.21), получим уравнение для f( , )

		ж d 2u					ц
		l з					ч
¶	f				2
		и dy					ш
	-						0
¶		ж du ц
		з				ч
		и dy				ш0

¶f

¶

+		B		ж	¶f
				з
	ж du ц
				и ¶
	l з		ч
	и dy ш0

¶ f	-	¶f	¶	f ц	= 0 .	(12.23)
				ч
¶		¶	¶	ш

На основании гипотезы Кармана уравнение (12.23) не должно зависеть от величин l, B, (du/dy)0 и (d2u/dy2)0. Для выполнения этого условия необходимо, чтобы соблюдались соотношения

ж du

d 2u ц

ж du ц

l » з

ч

,

B » l з

ч .

(12.24)

dy

2

и dy

ш

0

и dy ш0

Карман предположил, что длина смешения

l =

du

d 2u

,

(12.25)

dy

dy2

где – безразмерная постоянная, которую определяют опытным путем.

Турбулентные касательные напряжения

¶

ў ¶

ў

B2 ,

(12.26)

m = - uўvў =

»

¶x

¶y

и с учетом того, что B l(du / dy), получим

m »

l

2 ж du ц2

з

ч .

(12.27)

и dy ш

Выражение (12.27), полученное на основе гипотезы Кармана, совпало с выражением (12.15), вытекающим из теории пути перемешивания Прандтля. Так как m B2, то для масштаба скорости получим с учетом (12.17)

B v* .