Динамика вязкого газа, турбулентность и струи

4.2. Уравнения Прандтля

51

Учитывая проведенные оценки, уравнение энергии для пограничного

слоя можно представить в следующем виде:

ж

¶T

¶T ц

ж ¶P

¶P

¶P ц

з

+ u j

ч

= Ec з

+ u1

+ u3

ч

+

¶t

¶x1

¶x3

и

¶x j ш

и ¶t

ш

1

¶ ж ¶T ц Ec

йж ¶u

ц

2 ж ¶u

ц2

щ

+

+

к

1

+

3

ъ.

(4.13)

з

ч

з

¶x2

ч

з

ч

ъ

Pr Re ¶x2 и ¶x2 ш Re

ки

ш

и ¶x2 ш

л

ы

Возвращаясь к размерным величинам, выпишем уравнения плоского стационарного пограничного слоя в общепринятых обозначениях:

ж	¶u		¶u ц		dP		¶	ж	¶u ц
зu		+ v	ч	= -		+		з	ч	,
	¶x				dx
и			¶y ш				¶y и ¶y ш

¶( u)

+

¶( v)

= 0,

¶x

¶y

ж

¶T

¶T ц

dP

ж

¶u ц

2

¶

ж

¶T ц

(4.14)

CP зu

+ v

ч

= u

+

з

ч

+

з

ч

,

¶x

dx

и

¶y ш

и ¶y ш

¶y и ¶y ш

P = RT ,

=(T ).

Вполученной системе содержится пять уравнений и пять неизвестных:

,u, v, T, .

4.2. Уравнения Прандтля

Для несжимаемой среды ( = const, М = 0) и для постоянной вязкости уравнения движения в общепринятых обозначениях примут вид

¶u		¶u	¶u			1 dP				¶2u
	+ u		+ v ¶y	= -					+	¶y2	,
¶t		¶x						dx
											(4.15)
			¶u +	¶v	= 0.
			¶x	¶y

Уравнения (4.15) впервые были выведены Прандтлем (Prandtl, 1904).

52	4. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ

Обозначим продольную скорость вдали от тела через V = V (x, t). Поперечную скорость примем равной нулю. Тогда, принимая во внимание, что распределение давления в пограничном слое совпадает с тем, которое было бы на поверхности тела в отсутствие пограничного слоя, получим уравнение

¶V	+V	¶V	= -	1	¶P .	(4.16)
¶t		¶x			¶x

Уравнение (4.16) задает скорость на внешней границе пограничного слоя. Его решением будет интеграл Коши–Лагранжа. В стационарном случае его решением будет интеграл Бернулли

V2 2 + P = const.

Тогда первое из уравнений Прандтля (4.15) для стационарного течения можно записать в виде

	¶u		¶u		dV		¶2u
u		+ v		= V		+	¶y2 .	(4.17)
	¶x		¶y		dx

Граничные условия требуют обращения в нуль скорости на стенке и асимптотического приближения к скорости невозмущенного потока V(x, t) при удалении от нее.

4.3.Интегральные характеристики пограничного слоя

Обсудим еще раз те преимущества, которые дает использование уравнений пограничного слоя. С математической точки зрения они существенно проще уравнений Навье–Стокса, но все еще сложны для решения, так как остаются нелинейными уравнениями. Допущения, положенные в основу вывода уравнений пограничного слоя, привели к тому, что давление можно считать постоянным поперек его толщины и определять из решения невязких уравнений. Оценки показали, что толщина пограничного слоя мала и в первом приближении для расчета внешнего течения ее можно не учитывать.

4.3. Интегральные характеристики пограничного слоя

53

В качестве характеристики расстояния, на которое невозмущенный поток оттесняется наружу от тела из-за торможения газа в пограничном слое за счет вязкости, вводят так называемую толщину вытеснения согласно определению

Ґ ж				u ц
* = т з1		-			ч dy.	(4.18)
0	и			ҐVҐ ш
Здесь индексом отмечены величины,				взятые из решения невязкой задачи.
Расход идеального газа через поперечное сечение толщиной						* равен потере

расхода из-за торможения газа в пограничном слое, т.е. из-за торможения газа в пограничном слое линия тока внешнего течения оттесняется на величину *. Фактически невязкий поток обтекает тело, толщина которого увеличена на *. Это обстоятельство позволяет вычислить следующее приближение для расчета пограничного слоя. Расчет невязкого течения во втором приближении ведется для тела, толщина которого увеличена на *, полученную в первом приближении. Затем снова рассчитывается пограничный слой. Толщина вытеснения представляет собой некоторую меру толщины пограничного слоя, более определенную, чем сама толщина . Обычно за принимают значение ординаты, для которой продольная скорость в данном сечении отличается на 1 % от скорости невозмущенного течения, что вносит некоторую неопределенность.

В дальнейшем будет встречаться еще одна условная толщина слоя – толщина потери импульса **. Она задается выражением

Ґ		u	ж			u ц
** = т
			з1	-			ч dy.	(4.19)
0		ҐVҐ и			VҐ ш
Легко показать, что через отрезок		** в отсутствие пограничного слоя прохо-

дило бы количество движения, равное потере импульса в пограничном слое из-за торможения газа, т. е. толщина потери импульса тесно связана с величиной сопротивления тела при ламинарном обтекании. Вычисление сопротивления тела при его движении в газе является одной из основных задач динамики вязкого газа. Оно определяется касательным напряжением

xy =	ж	¶u		¶v ц
	з		+	ч .	(4.20)
	и ¶y			¶x ш

54 4. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ

Так как ¶u¶y >> ¶v¶x , в выражении (4.20) останется только основной член

xy =	¶u	.	(4.21)
	¶y

Для вычисления сопротивления следует проинтегрировать выражение (4.21) на стенке по всей поверхности тела:

l
W = b т xy cos ds,	(4.22)
S =0

здесь l – высота обтекаемого цилиндрического тела; b – его ширина; – угол, образуемый касательной к поверхности тела с направлением скорости V набегающего потока; s – координата, измеряемая вдоль поверхности тела (рис. 4.1).

u(y)

V

ds

xy

x

Рис. 4.1

Так как сos ds = dx, где координата x направлена по скорости V, выражение (4.22) можно записать в виде

l	ж	¶u ц	dx.	(4.23)
W = b т	з	ч
x=0	и ¶y ш y =0

Таким образом, для вычисления сопротивления трения необходимо знать градиент скорости на стенке.

4.4. Отрыв пограничного слоя

55

4.4. Отрыв пограничного слоя

Потеря энергии и количества движения в пограничном слое приводит к замедлению потока и утолщению пограничного слоя. Если есть область возрастания давления, то поток в конце концов остановится, пограничный слой оторвется от поверхности. В точке отрыва касательное напряжение становится равным нулю, так что

ж	¶u ц	= 0.
з	ч
и ¶y ш y =0

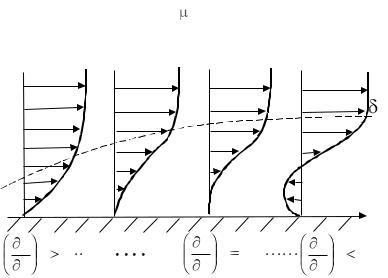
За точкой отрыва возникает медленное возвратное течение (рис. 4.2).

Отрыв пограничного слоя возможен только в зоне замедляющегося течения, т.е. в зоне с ¶P¶x > 0 . Действительно, в точке отрыва профиль скорости

должен иметь точку перегиба. Покажем, что появление точки перегиба возможно только при возрастании давления. Обратим внимание на то, что вторая производная скорости у внешней границы пограничного слоя всегда отрицательна. На поверхности тела, как это следует из уравнений Прандтля и граничных условий, выполняется следующее равенство:

	dP	=	ж	¶2u ц			.	(4.24)
			з		2	ч
	dx			¶y
			и			ш y =0

						(x)
						x
	u	0,	u	0	u	0.
	y		y		y
		0		0		0
			.
			Рис. 4.2

56	4. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ

Если течение разгоняется, то dPdx < 0 . И, как следует из (4.24),

¶2u¶y2 также меньше нуля на стенке, а значит, и везде в пограничном слое. Отсюда вытекает, что точки перегиба нет. Для замедляющего течения dPdx > 0 и ¶2u¶y2 > 0 на стенке и, значит, где-то в слое (где

¶2u¶y2 = 0) должна быть точка перегиба, а следовательно, и отрыв пограничного слоя.

Надо подчеркнуть, что уравнения пограничного слоя справедливы только до точки отрыва, за которой – область, где течение формируется за счет вязкости, значительно возрастает, и не выполняются осно вные предположения, положенные в основу вывода уравнений пограничного слоя. Вследствие образования ниже по течению завихренного следа сильно увеличивается общее сопротивление. Поэтому предсказание точки отрыва чрезвычайно важно, и его можно делать, основываясь на теории пограничного слоя.

4.5.Область применимости уравнений пограничного слоя

Приведенное в предыдущем разделе ограничение, связанное с отрывом пограничного слоя, не является единственным. Так как уравнения пограничного слоя выведены в предположении малости толщины пограничного слоя, т.е. для больших чисел Рейнольдса, само собой разумеется, что они несправедливы в окрестности передних кромок. Но и при больших числах Рейнольдса их надо применять с известной долей осторожности. Выведенные уравнения описывают ламинарные течения. При больших же числах Re течение переходит в турбулентное состояние, которое описывается другими уравнениями. Они будут рассматриваться ниже.

При выводе уравнения энергии не обсуждались ограничения на величину числа Маха и величина Ec/Re была принята 2 [см. уравнение (4.12)]. Легко показать, что Ec М2 и при умеренных числах Рейнольдса и достаточно больших числах Маха это условие нарушается.

4.5. Область применимости уравнений пограничного слоя							57
Оценим порядок величины M2/Re. Введем еще один характерный размер –
длину свободного пробега l. Для динамического коэффициента вязкости из кур-
са физики знаем следующую оценку:
			=	1	8	P l .	(4.25)
				2
Из (4.25) получим выражение для длины свободного пробега
		l = 1, 25				a ,
где a – скорость звука. Для больших чисел Рейнольдса можно составить сле-
дующее соотношение:
		l	= 1, 25			M .	(4.26)
						Re
Отношение длины свободного пробега к характерному размеру задачи
называют числом Кнудсена Kn = l				. Оно характеризует степень разреженно-
сти газа. Интересующая нас величина M2 Re » Kn2 и она не должна быть
М
		l/	= 10 l/		= 1		l/ = 0,01
12	С
	ляр				Течение
8					со сколь-
					жением
4							Обычная
							газовая
							динамика
0							6 lg Re
	–2	0		2		4
			Рис. 12.
				Рис. 4.3

58	4. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ

велика, т.е. уравнения пограничного слоя справедливы для не очень разреженных газов.

Пользуясь числом Кнудсена, можно весьма приближенно наметить области применимости различных методов описания течения газов. На рис. 4.3 показана диаграмма, разграничивающая области в зависимости от чисел M, Re и Kn.

Переходная область от обычной газовой динамики к свободномолекулярному течению разделена на две подобласти. Введена подобласть течения со скольжением. В ней еще применимы уравнения пограничного слоя, но уже видоизменены граничные условия для температуры и скорости. Принимается предположение о наличии на поверхности обтекаемого тела скачков скорости и температуры.

Задача 4.1

В случае равномерного отсоса пограничного слоя на пластине образуется асимптотический профиль отсасывания, не зависящий от продольной координаты. Определить профиль скорости, интегральные толщины пограничного слоя и напряжение трения.

Задача 4.2

Определить наименьший темп роста давления, при котором может произойти отрыв потока.

	5.2. Задача Блазиуса	59

5. АВТОМОДЕЛЬНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ

Автомодельными (подобными) решениями будем называть такие решения, для которых продольные составляющие скорости в двух различных поперечных сечениях отличаются друг от друга только масштабом ко-

ординат. В этом случае уравнения пограничного слоя могут быть сведены к обыкновенным дифференциальным уравнениям.

5.1. Решения Фокнера–Скэн

Рассмотрим стационарное течение несжимаемой жидкости в пограничном слое, когда

V (x) = cxm ,

(5.1)

где с и m – постоянные, причем m – безразмерная. Выражение (5.1) описывает симметричный потенциальный поток, омывающий клин с углом при вершине , где = 2m/(m+1). Если m > 0, то поток ускоряется и вершина клина x = 0 является точкой торможения. Для m = 0 получаем равномерный поток, омывающий полубесконечную плоскую пластину. В случае замедляющегося потока с m < 0 окрестность точки x = 0 должна быть исключена из рассмотрения.

Задача описывается системой уравнений

u	¶u	+ v	¶u	= V		dV	+	¶2u	,
	¶x		¶y			dx		¶y2
									(5.2)
			¶u	+	¶v	= 0
			¶x		¶y

60	5. АВТОМОДЕЛЬНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ПОГРАНИЧНОГО СЛОЯ
с граничными условиями
	u(0) = v(0) = 0, u(			) = V.		(5.3)
Введем функцию тока такую, что
	u =	¶	, v = -	¶	.	(5.4)
		¶y		¶x

При выполнении соотношений (5.4) уравнение неразрывности в системе (5.2) выполняется автоматически. Уравнение движения можно записать в виде

¶ ¶2

¶

¶2

dV

¶3

¶y

-

¶x ¶y2 = V

+

¶x¶y

dx

¶y3

с граничными условиями

¶

=

¶

= 0 при y = 0,

¶x

¶y

¶

= V

при y = .

¶y

Подставим (5.1) в уравнение (5.5) и сделаем замену переменных

й

m +1 V

(

x

)

щ1/ 2

й

2 xV

(

x

)

щ1/ 2

= к(

)

ъ

y;

= к

ъ f

( ).

2 x

m +1

л

ы

л

ы

Получаем уравнение Фокнера–Скэн (Folkner, Skann, 1931):

f ўўў + ff ўў +

(1 - f ў2 ) = 0

с граничными условиями

(

)

(

)

(

)

f

0

= f ў

0 = 0, f ў

Ґ

= 1.

Распределение скорости дается выражением u = V (x)

¶f / ¶

, =

2m

.

m +1

(5.5)

(5.6)

(5.7)

(5.8)

(5.9)