Динамика вязкого газа, турбулентность и струи

3.1. Обтекание шара. Приближение Стокса

41

3

x

3

V

(3.11)

p = -

V

= -

cos

.

2

r2

2

r0

0

Сила поверхностного трения по определению

¶U

(

) =

, где U =

u2 + v2 .

¶

Отсюда

3

3

V

U =

V

sin

и

(

) =

sin .

(3.12)

2

r

2

r

0

0

Полную силу, действующую на шар, получим интегрированием по по-

верхности шара с учетом направляющих углов

0

т л

( )

( )

ы

0 т

W = 2 r2

й

sin

- p

cos

щsin

Ч d

=

3 Vr

sin3 Ч d +

0

0

(3.13)

+3

Vr0 т cos2

sin

Ч d

= 4

Vr0 + 2

Vr0 = 6

Vr0.

0

Выражение (3.13) получило название формулы Стокса. Из (3.13) видно, что только треть всей силы сопротивления шара связана с силами давления.

Найдем коэффициент сопротивления шара

CW =	W		=	24	,	(3.14)
				Re
	S	V 2
		2

здесь S – площадь сечения; Re = VD/v – число Рейнольдса, рассчитанное по диаметру шара D = 2r0 .

Естественно попытаться построить решение для более простого двумерного случая – обтекания цилиндра. Существуют строгие доказательства того, что, оставаясь в рамках приближения Стокса, такое решение построить нельзя. В этом парадокс Стокса. Даже при малых числах Рейнольдса в плоской задаче обтекания нельзя полностью отбрасывать инерционные члены.

42	3. ПОЛЗУЩИЕ ДВИЖЕНИЯ

3.2. Обтекание шара. Приближение Озеена

Полученное в предыдущем разделе решение оказывается несправедливым на достаточно больших расстояниях от шара. Отброшенные в уравнениях Навье–Стокса инерционные члены порядка V2/r. Оставленные в уравнениях вязкие члены V/ r2. Условие

V / r2 >> V 2 / r

выполняется только на расстояниях
r << / V.	(3.15)

Таким образом, хотя составляющие скорости стремятся на бесконечности к своим истинным значениям, их распределения на больших расстояниях неправильны и их производные задаются плохо. Сопротивление же шара, вычисленное по формуле Стокса (3.14), дает хорошее приближение, так как определяется для малых значений r .

Для получения решений на больших расстояниях необходимо учесть инерционные члены. Проведем линеаризацию уравнений движения относи-

тельно возмущений равномерного	потока, внесенных присутствием шара
(C.W. Oseen, 1910). Пусть на бесконечности составляющие скорости		Vj = (V,
0, 0). Компоненты скорости потока можно представить в виде
u j	= V j + uўj .	(3.16)

Поправки uўj будем считать малыми величинами относительно V j . Под-

ставляя (3.16) в уравнения (1.20) и пренебрегая квадратичными членами, получим следующую систему уравнений:

	¶uў			¶P			¶2uў
V	i	= -				+	i ,	(3.15)
	¶x1			¶xi			¶x2j
			¶u j		= 0.			(3.16)
			¶x j

3.3. Течение в слое смазки							43
Граничные условия остаются преж-
ними. Из вида уравнений видно, что при
смене знака скоростей они уже не пере-
ходят сами в себя (из-за члена слева) и
описывают другое течение.
Решение		уравнений (3.15),				(3.16)
дает
CW =	24 ж			3	ц	(3.17)
		з1	+	16	Reч .		Рис. 7.
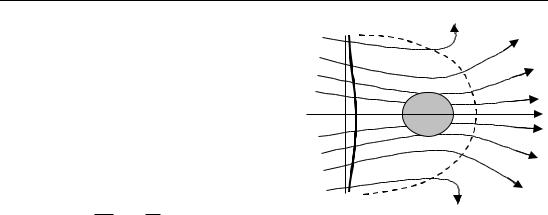
	Re и				ш		Рис. 3.2

Линии тока и распределение скорости по Озеену для наблюдателя, находящегося далеко от движущегося шара,

показаны на рис. 3.2. Картина линий тока не одинакова спереди и сзади тела. Жидкость вытесняется во все стороны. За шаром линии тока группируются плотнее, что указывает на формирование следа. Коэффициент сопротивления, рассчитанный по формуле (3.17), совпадает с экспериментальными данными до Re < 5.

3.3. Течение в слое смазки

Примером течения с преобладающим действием вязкости, важным для технических приложений, является течение смазочного масла в зазоре между движущимися частями машин. Течение вязкого масла в узком зазоре между цапфой и подшипником обладает следующим свойством. Возникающая в зазоре разность давлений может стать настолько большой, что результирующая сила будет поддерживать цапфу, и она не будет соприкасаться с подшипником. Наиболее существенные особенности течения в узком зазоре можно рассмотреть на простом примере ползуна и плоской опоры.

Рассмотрим две плоскости, образующие между собой малый угол (рис. 3.3). Верхняя плоскость (ползун) неподвижна, нижняя (опора) – дви-

	44			3. ПОЛЗУЩИЕ ДВИЖЕНИЯ
			жется со скоростью V в направлении
		Ползун	оси x. В направлении z опора и ползун
			имеют очень большую протяжен-
	h(x)		ность. В направлении y между ползу-
			ном и опорой	образуется тонкая кли-
			нообразная щель шириной		h(x). Бу-
			дем считать, что h << l, где l – длина
	l	Опора	ползуна. Рассмотрим отношение сил
		а	инерции к силам вязкости. Из членов,
		Рис. 3.3	зависящих от вязкости, наиболее су-
			щественный	¶2u / ¶y2 , тогда

	¶u	¶2u		Vl ж h ц				2
u		¶y2	=		з		ч	<< 1,	(3.18)
	¶x				и l ш

т.е. если Re = Vl / не очень велико, выражение (3.18) будет малой величи-

ной. Поскольку зазор мал, можно считать, что v << u. Оценим вторые производные в уравнении Навье–Стокса:

¶2u ¶2u			V V			ж h ц			2
		=				= з		ч	<< 1.
¶x2 ¶y2			l2 h2
						и l ш

В результате из уравнений движения останется только уравнение

¶P = ¶2u . ¶x ¶y2

Уравнение неразрывности запишем в интегральной форме

h

Q = т udy = const,

0

(3.19)

(3.20)

(3.21)

где Q – количество жидкости, протекающее в единицу времени через поперечное сечение щели.

3.3. Течение в слое смазки					45
Граничные условия имеют вид
u = V		при	y = 0,
u = 0		при	y = h(x),		(3.22)
P = P0 при			x = 0,	x = l.
Мы приняли, что давления в начале и в конце ползуна совпадают.
Интегрирование (3.20) по y дает
u =	1	¶p y2 + C y + C ,			(3.23)
2		¶x	1	2

где С1 и С2 – константы интегрирования. Используя два граничных условия на скорость (3.22), получаем

u = V (1 - y h) -	h2		dP		y	(1 - y h).	(3.24)
	2		dx		h

Градиент давления является функцией координаты x, и его надо определить.

Из (3.21) и (3.24) находим

dP		ж	V			Q	ц	(3.25)
	= 12	з			-		ч .
				2		3
dx		и 2h				h	ш

Интегрируя выражения (3.25) по х, получаем

x	x
P (x) = a + 6 V т h-2dx -12	Qт h	-3dx.	(3.26)
0	0

Константы a и Q находим из граничных условий (3.22) для давления:

			V	l	l
	a = P0 ,	Q =		т h-2dx / т h-3dx.		(3.27)
		2		0	0

Таким образом, если задано уравнение для зазора между ползуном и опорой и скорость движения опоры, то из (3.27) можно найти количество протекающей жидкости Q и тем самым из (3.26) – распределение давления.

46					3. ПОЛЗУЩИЕ ДВИЖЕНИЯ
P	P0				Зная распределение давления, можно
					вычислить силы, действующие на пол-
Рср					зун.
					Пример течения в щели между
	1				ползуном и опорой дан на рис. 3.3, а
					распределение нормированного на сред-
					нее значение давления в зазоре – на рис.
					3.4. Видно, что около неподвижной по-
					верхности возникает возвратное тече-
	0	0,4	0,8	х/l	ние. Оценка среднего давления под пол-
		Рис. 9.			зуном показывает, что оно приблизи-
		Рис. 3.4			тельно равно (l/h)2 и может достигнуть
очень больших величин.

Задача 3.1

Облако мелкодисперсных частиц радиусом R равномерно опускается на землю. Оценить скорость снижения облака в зависимости от числа Рейнольдса Re.

Задача 3.2

Найти положение максимума давления на опору в клиновидном зазоре (рис. 3.3), если его высота определяется соотношением h(x) = ( a– x).

Задача 3.3

Две параллельные круглые пластинки радиусом R расположены одна над другой на малом расстоянии h друг от друга, и пространство между ними заполнено жидкостью. Пластинки сближаются со скоростью u, вытесняя жидкость. Найти силу сопротивления сближению пластинок.

	4.1. Уравнения пограничного слоя	47

4. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ

В данном разделе мы будем рассматривать течения, формирующиеся при больших значениях числа Рейнольдса. Большие числа Рейнольдса эквивалентны очень малой вязкости, и газ можно рассматривать как иде-

альный. Однако такое приближение непригодно для описания течения газа вблизи твердых поверхностей. Граничные условия для идеальной жидкости требуют обращения в нуль на поверхности только нормальной составляющей скорости. Для вязких реальных газов на поверхности должна обращаться в нуль и продольная составляющая. Для того чтобы выполнить это условие, Прандтль предложил в пределах тонкого пограничного слоя газа, примыкающего к телу, считать, что скорость изменяется от нуля на поверхности до скорости невозмущенного обтекания идеальным газом. Падение скорости в пограничном слое обусловлено вязкостью газа, которой нельзя пренебречь, несмотря на большие значения числа Рейнольдса. В этом слое происходит интенсивное вихревое движение и вязкие силы соизмеримы по величине с инерционными. Математически это проявляется в том, что из-за больших градиентов скорости в тонком пограничном слое вязкие члены в уравнениях движения, содержащие производные скорости по координатам, велики, несмотря на малость .

4.1. Уравнения пограничного слоя

Следуя Прандтлю, разделим течение газа на две области. Первая – очень тонкий пограничный слой в непосредственной близости к поверхности обтекаемого тела, в котором существенны силы вязкости. Вторая – все осталь-

48	4. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ

ное течение, где вязкость несущественна. Будем считать, что течение во второй области нам известно. Выведем уравнения, описывающие движение газа в первой области.

Обратимся к безразмерной форме записи уравнений движения вязкого газа (1.45). Оценим отдельные члены, входящие в эти уравнения. Для упрощения записи опустим штрихи в обозначении безразмерных переменных. Примем для простоты, что характерные масштабы скорости и расстояния u и L 1. В направлении x1 и x3 на расстояниях L (характерного размера тела) скорость меняется медленно. Поэтому можно принять, что

¶		¶2		» 1 и	¶	¶2		» 1.	(4.1)
		»				»
	¶x1		¶x2		¶x3		¶x2
		1				3
Для компонент скорости, плотности и давления примем следующие
оценки:
		u1 » u3 » 1,			» 1, P » 1.				(4.2)

Ввиду малой толщины пограничного слоя ясно, что течение в нем будет происходить в основном параллельно обтекаемой поверхности. Скорость, направленная по нормали к поверхности u2, будет мала по сравнению с продольной u1 и трансверсальной u3 скоростями. Мы не рассматриваем нестационарного течения. Тогда из уравнения неразрывности имеем

¶u1 +

¶u2

= 0,

(4.3)

¶x1

¶x2

откуда следует, что если x2 << x1 , то u2 << u1 .

Если толщина динамического пограничного слоя

<< L, то из уравнения

неразрывности получим

1

ж ¶( u1)

¶

( u3 )ц

u2 » -

т

з

+

ч dx2

»

.

(4.4)

¶x1

¶x3

0

и

ш

Оценка производных по нормальной координате дает

¶

»

1

,

¶2

»

1

.

(4.5)

¶x2

¶x2

2

2

4.1. Уравнения пограничного слоя

49

Рассмотрим уравнения движения для i = 1 и 3. Подставим в них оценки (4.1) – (4.5). Нетрудно видеть, что с учетом принятых предложений все инерционные члены (левые части уравнений) одного порядка ( 1). В правых частях

уравнений члены 1 ¶P – также 1.

¶xi

Рассмотрим теперь члены в правой части уравнений, определяемые вязкостью. Так как пограничный слой формируется под действием сил вязкости, то хотя бы один из вязких членов уравнения движения должен быть одного порядка с инерционными членами. Оценки показывают, что таким членом будет

1 ¶			ж	¶u	ц		1 1
			з	i	ч	»				» 1.
				¶x2			Re	2
Re ¶x2 и					ш

Остальные вязкие члены 1/Re, и ими можно пренебречь. Для i = 1, 3 получим следующие уравнения:

	¶u		¶P		1 ¶			ж	¶u	ц
u j	i	= -		+				з	i	ч .
			¶xi
	¶x j				Re ¶x2 и ¶x2 ш

(4.6)

(4.7)

Соотношение (4.6) дает оценку для безразмерной толщины пограничного слоя: » 1Re . Если число Рейнольдса достаточно велико, так что мало,

то внешнее потенциальное обтекание будет только слегка нарушаться и в первом приближении для расчета внешнего течения можно считать, что пограничный слой отсутствует.

Рассмотрим теперь второе уравнение движения (i = 2). Подставим в него оценки (4.1) – (4.5) и учтем соотношение (4.6). Получим, что ¶P¶x2 » . То-

гда разность давления на стенке и в потоке			P » т	¶P	dx2 » 2	и в рассматри-
				¶x
			0	2
ваемом приближении можно принять
	¶P	= 0.				(4.8)
	¶x2

Из сказанного следует, что давление в пограничном слое равно давлению в основном потоке газа и может быть получено из решения невязкой задачи.

50	4. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ

Произведем теперь аналогичную оценку для членов уравнения энергии (1.35). Пусть T – безразмерная толщина температурного пограничного слоя, малая по сравнению с характерными размерами тела, одного порядка с . Из оценок для членов, зависящих от конвекции и трения, видно, что членами

¶ж ¶T ц

зч

¶x1 и ¶x1 ш

¶ж ¶T ц »

зч

¶x2 и ¶x2 ш

и	¶	ж	¶T ц		можно пренебречь по сравнению с
		з		ч
	¶x3	и	¶x3 ш

12 . Перенос тепла вследствие теплопроводности будет одного

T

порядка с переносом тепла из-за конвекции только в том случае, если выполняется соотношение

T2 »

1

,

(4.9)

Re Pr

что непосредственно следует из оценки члена

1

¶ ж

¶T ц

в уравнении

з

ч

Re Pr

¶x2 и

¶x2 ш

(1.35). Cвязав это соотношение с (4.6) для толщины динамического погранич-

ного слоя, получим

T

»

1

.

(4.10)

Pr

Для газов число Прандтля близко к единице, т. е. толщина температурного пограничного слоя действительно одного порядка с толщиной динамического.

Оценка остальных членов в уравнении (1.35) показывает, что в диссипа-

тивной функции следует сохранить	только	члены (¶u1 ¶x2 )2 » 1 2 и
(¶u3 ¶x2 )2 » 1 2 . Следовательно,
e » 1	2 .	(4.11)
ij ij

Таким образом, тепло, возникающее вследствие трения, существенно только при условии Ec »1, тогда член

Ec	(4.12)
Re ijeij » 1

будет одного порядка с членами, зависящими от конвекции и теплопроводности.