Динамика вязкого газа, турбулентность и струи

15.1. Шум турбулентных дозвуковых струй			161
Прибавляя и вычитая в правой части (15.3) выражение	¶2	c02	ij , получим
	¶xi¶x j

основное уравнение шумообразования без каких-либо допущений, так называемое уравнение Лайтхилла

¶2

- c2

¶2

¶Q

¶F

¶2Tij

¶t2

=

-

i +

,

(15.4)

0

¶x

2

¶t

¶xi

¶xi¶x j

i

где

T

=

u u

j

+ p

- c2

ij

(15.4а)

ij

i

ij

0

так называемый тензор Лайтхилла. Здесь c02 – скорость звука в среде. Члены в

левой части уравнения (15.4) являются волновым уравнением и описывают распространение звуковой волны в покоящейся среде. Члены, представленные в правой части уравнения (15.4), являются источниковыми членами и показывают причины (источники) шума струйного потока. Если имеют место радиальные сжатия и расширения среды по времени, то они порождают шум монопольного характера (член с Q). Если имеются силы (член с Fi), переменные в пространстве (например, вращающиеся лопасти винта в воздухе), то они тоже являются источниками шума дипольного характера. Последний член в правой части (Tij) отражает влияние тензора напряжений, который представляет собой разницу между напряжениями в потоке (первые два члена тензора) и напряжениями в однородной покоящейся среде (третий член – это просто статическое давление из соотношения для скорости звука). Член Tij отвечает за генерацию потоком квадрупольной составляющей шума, характерного для шума высокоскоростного турбулентного потока. Рассмотрим по отдельности источники шума, порождаемые аэродинамическим потоком.

15.1.2. Излучение звука монополями

Пусть в правой части уравнения (15.4) останется только расходный член с Q, ответственный за изменение производительного источника шума. Решением его будет уравнение

1

¶

ж

ц

dV

=

x

- y

т

Q з y, t -

ч

.

2

¶t

4 c0

V

и

c0 ш

x

- y

162			15. ШУМ СТРУЙ
Здесь		– переменная составляющая плотности; V – объем, занимаемый ис-
точником звука; y, x – вектор до некоторой точки в объеме источника звука и
вектор		до точки	регистрации звука вне объема источника звука. Вектор
( x	- y ) соединяет точку в объеме источника звука с точкой регистрации звука

вне объема. Будем для простоты рассматривать звуковое поле на больших расстояниях от источника, когда расстояние до него много больше его характерного размера r >> L. Решением уравнения (15.4) в этом случае является соотношение для пульсаций плотности

@	1		¶	ж		r ц dV
		т		Q з y, t -			ч		.	(15.5)
	2
		V	¶t	и		c	ш	r
	4 c0					0

Здесь y, r – соответственно координата элемента в объеме источника и коор-

дината приемника звука на большом расстоянии вне источника. Уравнение (15.5) описывает суммарные пульсации плотности, порождаемые локальными источниками пульсаций расхода Q размера dV в объеме V на расстоянии r от этого объема. Член после запятой в скобках под интегралом описывает задержку во времени прихода возмущений плотности в точку измерения.

Так как механическая мощность любого процесса пропорциональна произведению силы на скорость, то для мощности излучаемого звука получаем

Wзв = pакuакS.

Здесь S – площадь поверхности вокруг источника звука: рак и uак – значения звукового давления и скорости газа в звуковой волне на границе поверхности. Используя соотношение для скорости воздуха в акустических пульсациях uак,

uак = pак .

c0

Здесь с0 – акустический импеданс среды, или акустическое сопротивление, где 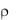– средняя величина плотности, и используя уравнение состояния

p = RT и выражение для скорости звука

c2

=

RT , получаем

0

p2

S

2R2T 2S

2c4S

» 4 r2c3

2

W =

ак

»

»

0

.

(15.6)

зв

c0

c0

c0

0

15.1. Шум турбулентных дозвуковых струй

163

Здесь площадь S выражена через расстояние до источника r. Здесь мы также неявно использовали предположение, что в звуковой волне температура меняется слабо и pак @ RT .

Если рассматривать частоты колебаний, когда длина звуковой волны много больше характерного размера L источника звука (вихря), т.е. >> L, то роль задержки времени в соотношении (15.5) будет незначительна и соотношение (15.5) можно переписать в виде

		V			¶Q
						¶t .	(15.7)
		4 c	2r
»
	0
Подставляя (15.7) в (15.6), получаем
		V 2			ж	¶Q ц	2
Wзв »					з	ч .
	4 c
					и	¶t ш
	0

Вводя в задачу характерную частоту колебаний f, характерную скорость течения потока U и характерный размер источника звука L, получаем для произ-

водной по времени ¶¶t » f » UL . Из уравнения (15.1) тогда получаем оценку для расхода Q » LU из размерности и первого и второго члена в левой части,

а V » L3 . Окончательно получаем

Wзв »		2U 4L6	» U 3L2M .	(15.8)
		c0 L4
4

Известно, что характерный масштаб турбулентности пропорционален масштабу течения в целом. Поэтому величина турбулентных источников или вихрей L в струях будет пропорциональна диаметру сопла D, из которого истекает струя. Отсюда видно, что мощность дипольного источника в длинноволновом диапазоне, где, по данным экспериментальных измерений, всегда наблюдаются максимальные значения интенсивности звука, будет пропорциональна суммарному потоку энергии газа ( U3D2) и числу Маха М:

Wзв » U 3D2M .

164	15. ШУМ СТРУЙ

Следует заметить, что здесь под числом Маха подразумевается число Маха конвекции вихрей в слое смешения струи, а не число Маха на оси струи. Последнее примерно в два раза больше числа Маха конвекции, что позволяет использовать это и последующие соотношения до чисел Маха собственно струи, равного двум. Эту зависимость иногда называют «законом четвертой степени» от скорости, что легко видеть из (15.8).

К аэродинамическим источникам звука преимущественно монопольного характера можно отнести: выхлоп поршневых двигателей, воздушные сирены, кавитационные явления в жидкостях, шум закипающей воды, шум газовых горелок, горячих дозвуковых струй и факела ракетных двигателей. Это связано с радиальными колебаниями элементарных объемов в потоке под воздействием точечных пульсаций давления или нагревания и охлаждения объемов. Схема движений в монополе и диаграмма направленности звука показаны на рис. 15.1. Как видно из рисунка, диаграмма направленности излучения монополя изотропна.

const

+

Монополь

Рис. 15.1

15.1.3. Излучение звука диполями

Оставим теперь в правой части уравнения (15.4) только второй член с Fi, ответственный за изменение массовых сил. Тогда решение волнового уравнения (15.4) будет

=

1

¶

ж

r ц dV

т

Fi з y, t -

ч

.

(15.9)

2

¶x

c

и

ш

r

4 c0

i V

0

15.1. Шум турбулентных дозвуковых струй

165

Как и ранее, будем рассматривать длинноволновое приближение, когда за-

держкой времени и, следовательно, членом r в аргументах функции Fi мож- c0

но пренебречь. Внесем производную по координате х под интеграл и продифференцируем подынтегральное выражение

¶

Fi ( y, t)

¶Fi ¶t 1

¶ 1 ¶Fi 1

1

»

+ Fi

=

- Fi

.

¶xi

r

¶t ¶xi r

¶xi

r

¶t

c0r

r2

На больших расстояниях от источника звука второй член в правой части соотношения становится значительно меньше первого. Тогда соотношение (15.9) можно преобразовать к виду

		1	¶			(15.10)
		4 c3r	т ¶t FidV
	»
		0

или в виде соотношения для порядков для производной по времени и оценки величины Fi из (15.2) получаем

	»	V		¶Fi	»	L3U U	2	.	(15.11)
		4 c3r		¶t		c3rLL
		0				0

Подставляя выражение (15.11) в соотношение (15.6), получаем зависимость для мощности дипольного источника шума потока

Wзв »	U 6L2	= U 3L2M 3 » U 3D2M3.	(15.12)
	c3
0

Из соотношения видно, что мощность пропорциональна суммарной энергии потока (первые три сомножителя) и числу Маха в третьей степени. Следовательно, с увеличением скорости потока интенсивность дипольных источников растет быстрее монопольных. Эту зависимость иногда называют «законом шестой степени» от скорости (см. (15.12)).

Модель диполя можно представить в виде тела, пульсирующего вдоль выделенной оси. Схема движений в диполе и диаграмма направленности приведены на рис. 15.2. Как видно из рисунка, диаграмма направленности имеет два максимума и минимум на оси симметрии колебаний объема. Вдоль оси

166	15. ШУМ СТРУЙ

симметрии пульсации плотности, приходящие с правой и левой грани, равны по величине и противоположны по знаку. Поэтому пульсации взаимно уничтожаются, образуя минимум интенсивности. Диполь можно представить также и в виде системы из двух монополей, пульсирующих в противофазе по времени. Такая система также будет давать диаграмму направленности типа рис. 15.2.

cos

+		–
–		+

Диполь

Рис. 15.2

К аэродинамическим источникам звука преимущественно дипольного характера можно отнести: вентиляторы, компрессоры, газовые турбины, воздушные винты, обтекаемые поверхности каналов и летательных аппаратов.

15.1.4. Излучение звука квадруполями

Оставим теперь в правой части уравнения (15.4) только третий, тензорный член. Тогда решением уравнения будет выражение

=		1
		c2
4
		0

¶2 ¶xi¶x Vт

ж	r	ц
Tij з y, t -		ч
	c0
и		ш	dV .	(15.13)
r

Здесь, так же как и для случая монополя и диполя, выражение (13.13) описывает суммарные возмущения плотности, порождаемые взаимодействием турбулентных вихрей (первый член тензора Tij) и вязкими напряжениями в турбулентном потоке (второй член этого тензора) в элементарных объемах dV общего объема области генерации звука V на расстоянии r от него. В предположении низкочастотных волн и пренебрегая задержкой сигнала от различных точек объема, внесем последовательно производные по координа-

15.1. Шум турбулентных дозвуковых струй

167

те х под интеграл и продифференцируем подынтегральное выражение по аналогии со взятием производных в подразделе 15.1.3. Тогда получим выражение нового вида

1

1

й

1

¶2T

3

¶T

3T щ

»

т

к

ij

+

ij

+

ij

ъ dV .

4 c2r

¶t2

V

r

кc2

c0r ¶t

r2 ъ

0

л

0

ы

Для больших расстояний от источника звука второй и третий члены под интегралом становятся много меньше первого и это выражение сворачивается к виду

	1				¶2Tij			(15.14)
»	4 c	4	r	т	¶t	2 dV .
	0

Поясним физику образования квадрупольного шума в турбулентном потоке. Оценка величины членов в тензоре Tij показывает, что член вязких напряже-

	ний pij пропорционален величине	1	и при обычных условиях истечения
		Re

струй значительно меньше первого члена Tij » uiu j , описывающего напряжения Рейнольдса. Фактически тензор Tij » uiu j – это количество движения

единичного объема ui в направлении xi, переносимое со скоростью uj в направлении xj. Так как перенос симметричен во все стороны, то элемент жидкости, находящийся под действием импульса ui, испытывает с двух сторон воздействие равных по величине, но противоположно направленных сил. Как было отмечено ранее, воздействие силы на элемент среды эквивалентно эффекту дипольного источника. Пара равных по величине и противоположных по направлению сил эквивалентна двум противоположно ориентированным диполям, т.е. квадруполю. Интенсивность квадруполей характеризуется тензором плотности количества движения Tij. Схема генерации квадруполей и направленность излучения звука показаны на рис. 15.3. Если квадруполь продольный и диполи, образующие его, параллельны друг другу и пульсируют в противофазе, то диаграмма направленности пропорциональна квадрату косинуса, так как направленность диполя пропорциональна косинусу угла. Если квадруполь поперечный, то излучение одного из диполей сдвинуто на 90и диаграмма

168	15. ШУМ СТРУЙ

направленности представляет собой произведение косинуса на синус. В свою очередь квадруполь можно показать в виде системы из четырех диполей, пульсирующих парами в противофазе (продольный квадруполь) или каждый относительно другого со сдвигом по фазе на 90 (обычный квадруполь).

–	+	+	–		+	–
					–	+

cos2 sin

cos2

Продольный	Поперечный
квадруполь	квадруполь

Рис. 15.3

Используя порядковые оценки для производных по времени и порядковую оценку для тензора Tij из соотношения (15.4а), получаем после подстановки оценок в (15.14) для пульсаций плотности:

»	U 2 U 2L3	=	U 4L	.	(15.15)
	c04rL2		c04r

Подставляя (15.15) в (15.6) получаем для звуковой мощности квадрупольного источника выражение

Wзв »	U 8L2	» U 3L2M5 » U 3D2M5.	(15.16)
	c5
0

Из (15.16) видно, что с ростом числа Маха мощность излучения квадрупольных источников опережает все остальные. Это известный «закон восьмой степени» от скорости, справедливый для чисел Маха струй вплоть до двух.

Примером шума преимущественно квадрупольного характера может служить шум реактивных и высокоскоростных воздушных струй.

15.1. Шум турбулентных дозвуковых струй

169

15.1.5.Влияние конвекции на направленность излучения шума

Так как монопольное излучение изотропно, а ориентация диполей и квадруполей случайна, то шум струи должен быть также практически изотропным. Небольшая неизотропия возможна только из-за наличия длины струи. Тем не менее из-за движения потока в излучении звука появляется выделенное направление и влияние его на направленность звука стано вится тем больше, чем больше скорость. Так как при больших скоростях, но меньших скорости звука в слое смешения, излучают преимущественно квадрупольные источники турбулентного потока, то имеет смысл рассмотреть только этот случай. Решением уравнения (14.4) без упрощений будет соотношение

ж

ц

x

- y

2

Tij з y, t

-

ч

c0

=

1

¶

т

и

ш

dV .

(15.17)

2

4

c

¶x ¶x

j

x

- y

i

0

V

Из-за движения источника звука он непрерывно меняет свое местоположение и эффективный объем вихря вытягивается в направлении движения. Введем новую координату , которую он имел на момент излучения звука:

		+ Mк			.	(15.18)
	= y		x	- y

Здесь Мк – число Маха скорости конвекции источника звука в потоке. Тогда соотношение для дифференциалов объемов источника будет

			d
dV (		) = dV ( y)			,
			dy

или с учетом (15.18)

			м		Mк (xi - yi )ь
dV (		) = dV ( y)н1		-				э .
			п			x	- y	п
			о					ю

170

15. ШУМ СТРУЙ

Уравнение (15.17) в этом случае запишется так:

1

¶2

ж

ц

dV ( )

=

т

x

- y

Tij з

, t -

ч

- Mк (xi - yi )

.

(15.19)

4 c2

¶xi¶x j

и

c0 ш

x

- y

0

V

Внося последовательно производные по координате х под интеграл аналогично действиям, выполненным в разд. 15.1.4, получим под интегралом три члена. Из них на большом расстоянии не малым будет только первый член со второй

производной по времени и по координате хi, хj только второго аргумента в тен-

зоре. Поскольку производная по координате хi

от модуля вектора

при

x

- y

постоянном

и с использованием (15.18) дает

¶

x

- y

=

xi - yi

,

¶xi

- Mк (xi - yi )

x - y

уравнение (15.19) можно преобразовать:

1

(xi - yi )(x j - y j )

¶2

ж

ц

x

- y

ч dV ( ).

4 т

2 Tij з , t -

=

{

- yi )}

3

4 c0

x

- y

- Mк (xi

¶t

и

c0 ш

Вводя угол

между направлением на точку регистрации звука и направлением

движения источника сos ( )

(xi - yi )

=

, получим

x - y

1

(xi - yi )(x j - y j )

¶2

ж

ц

x

- y

ч dV ( ).

4 т

2 Tij з , t -

=

{1 - Mксos ( )}

3

3

4 c0

x

- y

¶t

и

c0 ш

» r; (xi, j

- yi, j ) » xi, j » r и за-

На больших расстояниях от источника

x - y

паздыванием по времени можно пренебречь. Тогда

1

¶Tij

4

3 т

2 dV .

(15.20)

=

4 c0 r (1 - Mксos )

V

¶t