Динамика вязкого газа, турбулентность и струи

8.4. Общий подход к проблеме пространственного пограничного слоя

81

ристическое уравнение. Полученные в результате характеристики он н а- звал субхарактеристиками. Поскольку в уравнениях движения старшими станут теперь первые производные, характеристическое уравнение запишется в виде

S

0

0

0

0

S

= 0 ,

(8.18)

¶Q

¶Q

¶Q

¶x

¶y

¶z

ж

¶

¶

¶ ц

где введено обозначение

S =

зu

+ v

+ w

ч Q .

Раскрывая определитель,

и

¶x

¶y

¶z ш

получим уже знакомый нам корень

¶Q

= 0 и новый S = 0 . Нетрудно видеть,

¶y

что последний корень соответствует линии тока в трехмерном потоке.

Таким образом, нами получено, что возмущения в некоторой точке P (рис. 8.5) пространственного пограничного слоя с бесконечной скоростью распространяются вдоль нормали AB к обтекаемой поверхности и далее они рас-

Область зависимости А Область

влияния

Р

Поток

В

Характеристики

Проекции

субхарактеристик

Рис. 8.5

82	8. ТРЕХМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ

пространяются по потоку вдоль каждой линии тока, проходящей через эту нормаль. И с этих линий тока возмущения опять же распространяются по нормалям, проведенным через каждую их точку. Отсюда следует простое правило для зоны влияния данной точки: через нее надо провести нормаль к обтекаемой поверхности и через нее построить две поверхности, содержащие крайние линии тока, перпендикулярно обтекаемой поверхности. Область, заключенная между ними, и будет зоной влияния данной точки. Аналогично строится и зона зависимости, но только против потока.

Из такого представления о построении зоны влияния вытекает простое правило задания граничных условий на боковых границах рассматриваемой области. На каждой границе следует задавать все три компоненты скорости, если газ втекает через нее в рассматриваемую область, в противном случае граница свободна от граничных условий. Как и в двумерном случае, на обтекаемой поверхности необходимо задать все компоненты скорости, а на внешней границе – все компоненты, кроме нормальной к ней.

В случае сжимаемого газа к системе уравнений (8.16) добавляется уравнение энергии, содержащее температуру. Эта система имеет те же характеристические свойства. Поэтому правило задания граничных условий на боковых границах для нее сохраняется с той лишь разницей, что к заданию компонент скорости добавится температура. Ее задание добавится также на стенке и внешней границе.

8.5.Аналогия между теплопередачей

исопротивлением тела

Все решения уравнений двумерного ламинарного пограничного слоя в несжимаемой жидкости для распределения скорости будут иметь вид

u		ж x			y			ц	(8.19)
	=	f1 з		,			Reч .
UҐ		и l			l			ш

8.5. Аналогия между теплопередачей и сопротивлением тела

83

Аналогично все решения для профиля температуры будут иметь вид

T - T			ж x			y			ц
	Ґ	=	f2 з		,			Re, Prч .		(8.20)
T	- T		и l			l			ш
w	Ґ

Поэтому для плотности потока тепла к поверхности, используя (8.20), получим

T

x

q

Tw T

Re f2

, Pr .

y

y

0

l

l

Тогда для локального числа Нуссельта получим выражение

ql

f2

x

, Pr

Nu

Re

.

(8.21)

Tw T

l

С использованием выражения (8.19) для локального касательного напряжения получаем

	ж	¶u ц
0 =			=	UҐ	Re	f1	ж x ц
	з	ч					з		ч .	(8.22)
				l
	и ¶y ш		y =0				и l ш

Отсюда безразмерный локальный коэффициент сопротивления будет равен

cў

=

0

= 2

1

f

ж

x

ц .

(8.23)

f

2

Re

1

з ч

и l ш

UҐ

2

Скомбинируем (8.21) и (8.23) и в предположении одинаковой функциональной зависимости f для скорости и температуры получим

	Nu	1	c f Re f	x	, Pr .	(8.24)
		2		l

84	8. ТРЕХМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ

Это есть так называемая аналогия Рейнольдса в общей форме. Для течения на пластине при числе Прандтля, равном единице, профиль скорости и температуры совпадает. Тогда

	1	(8.25)
Nux =	2 cўf Rex .

Следует отметить, что аналогия Рейнольдса действует и в турбулентном течении.

Задача 8.1

Найти, какому плоскому течению соответствует течение в окрестности критической точки, где r(x) = x; U(x) = u1x.

	8.5. Аналогия между теплопередачей и сопротивлением тела	85

9. СПУТНОЕ ТЕЧЕНИЕ ЗА ПЛАСТИНОЙ

Рассмотрим течение в следе на большом удалении от тела. Для простоты примем за тело плоскую пластинку длиной l. Обозначим через V скорость однородного потока (рис. 21). Пример такого течения интересен тем, что уравнения пограничного слоя остаются справедливыми в отсутствие стенок, так как изменение характеристик течения вдоль по потоку происходит намного медленнее, чем поперек. Наличие стенки – не обязательное условие применимости уравнений пограничного слоя. Надо только, чтобы характерные поперечные размеры течения были намного меньше продольных размеров. Будем считать скорость небольшой, так что жидкость можно рассматривать несжимаемой, давление постоянным (P(x) = const). Тогда движение описыва-

ется системой уравнений

	¶u		¶u		¶2u
u	¶x	+ v ¶y		=	¶y2		,	(9.1)
		¶u	+ ¶v	= 0.
		¶x	¶y
Граничные условия
u( ) = V,		v(0) =			u		0.	(9.2)
					y y
							0

Последнее условие следует из симметрии течения.

Система (9.1) с граничными условиями (9.2) имеет очевидное решение u = V, которое означает, что на очень большом удалении от тела течение полностью выравнялось. Это решение нас не интересует.

Будем искать нетривиальное решение вдали от тела, для которого выполняется некоторый «закон сохранения». Обратимся к выводу интегрального условия импульсов (6.4). Интегрирование выражения (6.3) будем проводить в

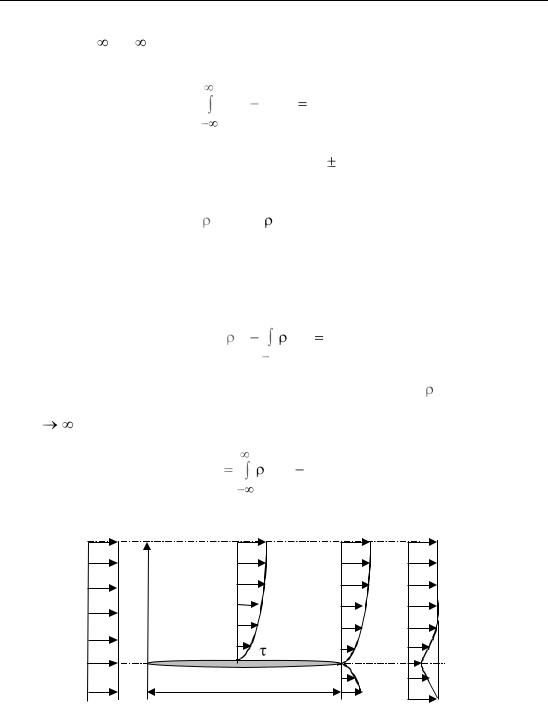
86 9. СПУТНОЕ ТЕЧЕНИЕ ЗА ПЛАСТИНОЙ

пределах от – до . Тогда с учетом того, что V = const, а (¶u¶y)Ґ-Ґ = 0 , получим

u V u dy const.

(9.3)

Для того чтобы выяснить физический смысл константы (9.3), применим теорему импульсов к прямоугольной области (L, h). На рис. 9.1 изображена ее верхняя половина. Проекция импульса на ось 0x дает

	h
2h V 2	- т u2dy -W = 0.	(9.4)

-h

Первый член равенства (9.4) определяет импульс на левой границе, а второй – на правой. Здесь W – лобовое сопротивление тела (потеря импульса за счет трения).

Уравнение постоянства расхода запишем в виде

		h
	2h V	udy 0.	(9.5)
		h
		h
Умножив (9.5) на V и вычтя из (9.4), получим, что W = т			u (V - u) dy , или
		-h
при y	:
	W	u V u dy .	(9.6)

V L

y

h

0

u’

l

Рис. 21Рис. . 9.1

87

Мы видим, что вдали от тела сохраняет свою величину интеграл (9.3), а из (9.6) следует, что этот интеграл равен лобовому сопротивлению тела.

Можно считать, что на большом удалении от тела величина u′ = V – u мала. Подставим ее в уравнение (9.1), граничные условия (9.2), условие (9.6) и проведем линеаризацию:

		¶uў		¶2uў
		V ¶x	=	¶y2		,			(9.7)
	ж	¶uўц				Ґ	W
uў(Ґ) = 0,				= 0,		т uўdy =		.	(9.8)
	з	ч
	и ¶y ш y =0				-Ґ		V

Введем автомодельную координату

		y					V		.
	=			Re = y						(9.9)
		x					x

Решение системы (9.7) с граничными условиями (9.8) будем искать в виде

ж x ц-1/ 2

uў = CV з ч g ( ). (9.10)

и l ш

Выбор решения в виде (9.10) надо признать удачным потому, что подстановка в (9.6) дает выражение

					Ґ
	W = C V 2		l
					т gd ,	(9.11)
			V
					-Ґ

которое не зависит от x, т.е. наш «закон сохранения» выполняется.

Подставив значение (9.10) в уравнение (9.7), получим обыкновенное дифференциальное уравнение

	g ўў +	1	g ў +		1	g = 0	(9.12)
		2			2
	с граничными условиями
	g (0) = 0,			g( ) = 0.			(9.13)

88			9. СПУТНОЕ ТЕЧЕНИЕ ЗА ПЛАСТИНОЙ
Интегрирование уравнения (9.12) дает
g ў +	1		g = const.
	2

Из первого граничного условия (9.13) получим, что const = 0. Второе интегрирование дает

g = Aexp (- 2 / 4).

(9.14)

Определим постоянную A из условия (9.11). Так как

	2 / 4 d
exp		2 ,

то	W 2		C V 2		l		,
					V

здесь C′ = CA = const.

Из решения задачи Блазиуса знаем, что

W = 1, 328 V 2 Vl .

Тогда решение задачи можно представить в окончательном виде:

uў		0,664 ж x ц-1/ 2						2
	=				з		ч	exp (-y V / 4x	).
V					и l ш

(9.15)

(9.16)

(9.17)

По форме решение (9.17) совпадает с кривой Гаусса. Сравнение с экспериментом показало, что решение (9.17) справедливо для x/L > 3.

Отметим, что рассмотренная задача о ламинарном спутном течении не имеет большого практического значения. Полученное решение справедливо на больших расстояниях от тела, однако течение в следе неустойчиво и достаточно быстро переходит в турбулентное состояние. Тем не менее на еще большем расстоянии след вновь ламинаризуется из-за вязкого затухания турбулентности.

	10.1. Линейная задача устойчивости	89

10. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ

Для большинства задач о движении вязкой жидкости в заданных стационарных условиях должно существовать точное стационарное решение уравнений гидродинамики. Эти решения формально существуют при

любых числах Рейнольдса. Но не всякое решение уравнений движения, даже если оно является точным, может реально воплотиться в природе. Движения не только должны удовлетворять гидродинамическим уравнениям, но еще и быть устойчивыми: малые возмущения, раз возникнув, должны затухать со временем или в пространстве. Если же, напротив, неизбежно возникающие в потоке жидкости сколь угодно малые возмущения стремятся возрасти, то движение неустойчиво и фактически существовать не может.

Математическое исследование устойчивости движения происходит по следующей схеме. На исследуемое стационарное решение (распределение скоростей, в котором пусть будет V0(xi) и давление р0(xi)) накладывается малое нестационарное возмущение скорости v1(xi, t), и давления р1(xi, t), которое должно быть определено таким образом, чтобы результирующее движение V = V0 + v1; р = р0 + р1 удовлетворяло уравнениям движения, начальным и граничным условиям. Уравнение для определения v1 и р1 получается подстановкой их в уравнения движения жидкости, причем считается, что известные функции V0 и р0 удовлетворяют стационарным уравнениям.

Полученная таким образом система дифференциальных уравнений в частных производных описывает поведение возмущений во времени и в пространстве. Поставив соответствующие начальные и граничные условия, эти уравнения надо проинтегрировать и определить, растут возмущения или нет, т. е. устойчиво движение или неустойчиво. В настоящее время такую задачу можно решить только для некоторых частных случаев, используя возможности современных суперЭВМ. Для ее решения продолжают созда-

90	10. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ

вать и совершенствовать теорию и численные методы. Однако предварительную информацию можно получить, основываясь на решении упрощенных уравнений.

10.1. Линейная задача устойчивости

Наибольшие упрощения возможны при рассмотрении бесконечно малых возмущений. В этом случае можно опустить члены высших порядков по малой величине v1 в уравнениях устойчивости и система значительно упрощается. Дальнейшее упрощение возможно при рассмотрении плоскопараллельных течений – течений, у которых стационарные решения V0 зависят только от одной переменной, скажем, y – нормальной к поверхности обтекаемого тела. Тогда v1 и p1 удовлетворяют системе однородных линейных дифференциальных уравнений с коэффициентами, являющимися функциями только от координаты y, но не от времени, и другой координаты x, направленной по потоку (для простоты рассматриваем двумерное течение, не зависящее от трансверсальной координаты).

Решение полученной системы уравнений можно искать в виде элементарных волновых решений, пропорциональных exp[i (х – сt)]. Граничными условиями является исчезновение v1 на твердой неподвижной поверхности и на бесконечном удалении от нее, т. е. граничные условия тоже однородны. При этом необходимо отыскать при заданном числе Рейнольдса Re значения фазовой скорости с и волнового числа , для которых линеаризованные однородные уравнения при однородных граничных условиях имеют нетривиальное решение, т. е. возникает задача на собственные значения. В процессе решения уравнения получается неявная зависимость между , Re и с, которую называют характеристическим уравнением D( , Re, с) = 0. В общем случае и с – комплексные числа и неустойчивость развивается во времени и в пространстве.

Можно разделить временную и пространственную неустойчивости. Для временной неустойчивости полагаем, что – вещественное число, а с = сr + iсi – число комплексное. Тогда решение будет неустойчивым, если сi > 0, и устойчивым, если сi < 0. Обычно эволюцию во времени любого возмущения, возникающего в момент времени t = 0, можно проследить, рассматривая его разложение по элементарным волновым решениям.

К ситуациям, практически реализуемым на летательных аппаратах, более подходит рассмотрение пространственной неустойчивости. Предполагается,