6.3. Интерполяционные формулы центральных разностей

Для функции y=f(x) заданной в равноотстоящих узлах центральные разности определяются соотношением

; ;, (6.10)

которое с учётом нисходящих и восходящих разностей имеет вид

y_-n, y_-n+1,…, y_-2, y_-1, y₀ , , y₁,y₂,…,y_k-1,y_n (4.11)

Узлы интерполирования в этом случае размещены симметрично относительно x₀, а их значения

, n.

Значение f(x) в точке x_i<x<x_i+1, не совпадающей с узлом интерполирования, может быть определено с помощью полинома Стирлинга

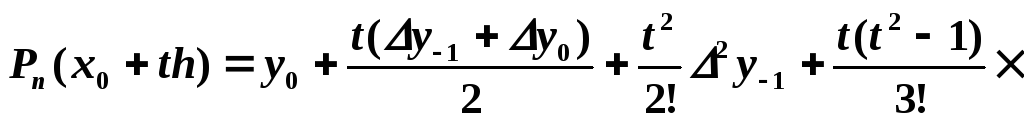
, (6.12)

где t=(x-x₀)/h , - центральные разности.

Погрешность формулы Стирлинга

. (6.13)

Формулу (6.12) используют для интерполирования в середине интервала [a,b], около конца и начала его (в последнем случае (6.12) даёт более точный результат). Центральную точку x₀ выбирают так, чтобы –0,5t0,5.

Знание центральных разностей позволяет использовать при интерполяции полином Бесселя

6.4. Интерполирование функции с не равноотстоящими узлами

Для произвольно заданных узлов интерполяции можно воспользоваться формулой Лагранжа или многочленом Ньютона. Интерполяционный полином Лагранжа имеет формулу

(6.14)

или в развёрнутом плане

(6.15)

Погрешность при вычислении определяется выражением

, (6.16)

где ; i=0,1,2, ..., n; формула (6.15) имеет большую точность для средних отрезков , она менее эффективна для крайних отрезков. Значения независимой переменной в формуле могут быть как равно-, так и не равноотстоящими.

Примеры

№1 Найти значение интерполирующего полинома для функции y=e^x заданной таблицей.

х	3,50	3,55	3,60	3,65	3,70
у	33,115	34,813	36,598	38,475	40,447

на интервале [3,5; 3,6] с шагом =0,05.

Решение. Составим таблицу с нисходящими конечными разностями для заданных точек функции y=e^x

х	у	Δу	Δ^2 у	Δ^3 у
3,50 3,55 3,60 3,65 3,70	33,115 34,813 36,598 38,475 40,447	1698 1785 1877 1972	87 92 95	5 3

Отмечаем, что значения конечных разностей третьего порядка примерно одинаковы, а это значит, что нужно использовать полином P_n(x) степени n=3. Для х₀=3,50 и у₀=33,115, мы имеем отыскиваемый полином в виде.

или с учетом значений

№2 Необходимо найти значение функции y(x) для x₁=1,2173 по данным таблицы.

x	y
1.215 1.220 1.225 1.230 1.235 1.240 1.245 1.250 1.255 1.260	0.106044 0.106491 0.106935 0.107377 0.107818 0.108257 0.108696 0.109134 0.109571 0.110008

Найдем для этого случая нисходящие конечные разности.

i	xi	yi	Δуi	Δ^2 уi
1 2 3 4 5 6 7 8 9 10	1.215 1.220 1.225 1.230 1.235 1.240 1.245 1.250 1.255 1.260	0.106044 0.106491 0.106935 0.107377 0.107818 0.108257 0.108696 0.109134 0.109571 0.110008	0.000447 0.000444 0.000442 0.000441 0.000439 0.000439 0.000438 0.000437 0.000437 -	-0.000003 -0.000002 -0.000001 -0.000002 0 -0.000001 -0.000001 0 - -

Отметим, что, начиная со второго порядка, конечные разности примерно одинаковы. Следовательно, воспользуемся полиномом Ньютона второго порядка, для x=1,2173.

№3 Пусть y_x функция заданная таблицей с неравноотстоящими значениями аргумента.

x	y
0,103 0,108 0,115 0,120 0,128 0,136 0,141 0,150	2,01284 2,03342 2,06070 2,07918 2,10721 2,13354 2,14922 2,17609

Нужно вычислить значение функции для x₁=0,112.

Воспользуемся формулой Лагранжа

где используются разделенные разности.

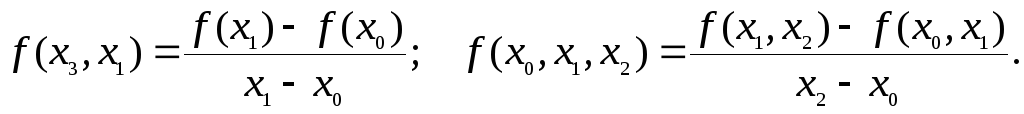
Составим таблицу этих разностей.

xi	yi	f(xi,xi+1)	f(xi,xi+1,xi+2)
0,103 0,108 0,115 0,120 0,128 0,136 0,141	2,01284 2,03342 2,06070 2,07918 2,10721 2,13354 2,14922	4,116 3,896142 3,696 3,503750 3,291250 3,136 -	-18,238166 -16,761833 -14,788461 -13,281250 -11,942307 - -

Затем определяем f(0,112) двумя методами, для x₀ равным соответственно 0,103 и 0,108:

В результате имеем f(0,112) ≈ 2,04922.

№4 Оттискать эмпирическую формулу для функции y_x заданной таблично.

X	9	1	2	3	4	5
y	5.2	8.0	10.4	12.4	14.0	15.2

Вычислим нисходящие конечные разности второго порядка

x	y	Δy	Δ^2 y
0 1 2 3 4 5	5.2 8.0 10.4 12.4 14.0 15.2	2.8 2.4 2.0 1.6 1.2	-0.4 -0.4 -0.4 -0.4

из таблицы видим, что , а это значит необходим полином Ньютона второй степени. Запишем его в виде

y = 5,2 + 2,8x – x(x – 1)

в итоге имеем

y = 5,2 + 3x – 0,2x².

№5 Пусть y_x заданна своими значенияи в нижеприведенной таблице. Необходимо вычислить значение y_x для аргумента x=0,304, используя полиномы Ньютона первого и второго порядков.

x	y
0,29	3,25
0,30	3,17
0,31	3,12
0,32	3,04
0,33	2,98
0,34	2,91

Полином Ньютона первого порядка

y(0,304) = y₀ + q∙Δy₀;

h(x) = x₁- x₀ = 0,31-0,30 = 0,01.

Δy₀ = y₁- y₀ = 3,12 - 3,17 = -0,05.

y(0,304) = 3,17 + 0,4 ∙ (-0,05) ;

y(0,304) = 3,15.

Полином Ньютона второго порядка

Δ²y₀ = Δ¹y₁ – Δ¹y₀ = 3,04 – 3,12 – (-0,05) = -0,03.

y(0,304) = 3,153.