3.4. Асимптоты

При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.

Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.

Следует отметить, что не любая кривая имеет асимптоту. Асимптоты бывают вертикальные, наклонные и частный случай наклонных – горизонтальные.

Вертикальные асимптоты

Из определения асимптоты следует, что еслиилиили, то прямаях = а – вертикальная асимптота кривой y = f(x).

Наклонные и горизонтальные асимптоты

Наклонная асимптота задается уравнением прямой y = kx + b, где коэффициенты k и b вычисляются по следующим формулам:

,

Если k =0, то получаем горизонтальную асимптоту.

3.5.Общая схема исследования функции и построение графиков

Графики функций строятся по точкам. Обычно из уравнения y=f(x) находят несколько точек графика функции y=f(x) и соединяют эти точки плавной кривой. Однако при таком методе легко пропустить какие-то важные особенности графика и допустить ошибку в построении.

Для построения графика функции нужно исследовать ее свойства. Процесс исследования функции состоит из нескольких этапов.

1. Область определения функции.

2. Координаты точек пересечения с осями координат.

3. Четность, нечетность функции.

4. Асимптоты графика и пределы на ±∞. (Если они имеются).

5. Критические точки.

6. Интервалы монотонности и точки экстремума.

7. Промежутки выпуклости и вогнутости, точки перегиба. (Если они имеются).

8. Дополнительные точки, если нет асимптот.

9. Построение графика.

10. Область значения функции.

3.6. Примеры

№1. Исследовать функцию на монотонность и экстремум .

Решение.

1. D(f)=R

2. 

3. при , , .

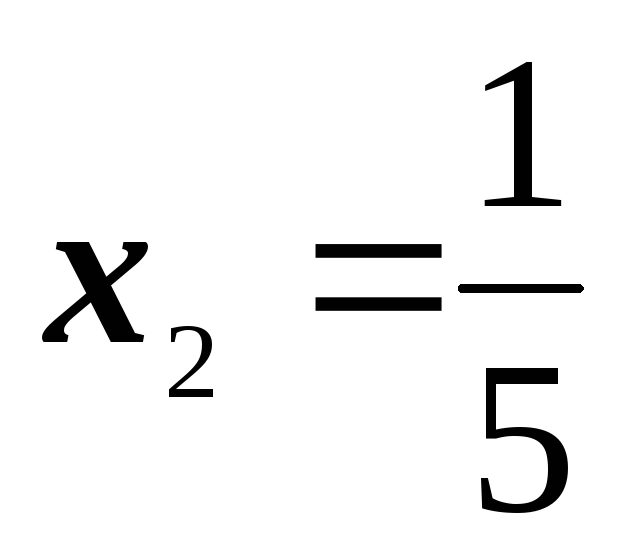–1, , 1 – критические точки, так как внутренние точки области определения и .

4. Выясним знаки производной:

Функция y=f(x) возрастает на промежутках (–∞; 1/5]; [1;+∞).

Функция y=f(x) убывает на промежутке [1/5; 1].

–точка максимума, f() – максимум функции.

1 – точка минимума, f(1) – минимум функции (рис. 3.6.1).

№2. Исследовать функцию на выпуклость и вогнутость. Найти точки перегиба: .

Решение.

1. D(f)=R

2. .

3. .

при .

Функция y=f(x) выпуклая на промежутке (–∞; 2].

Функция y=f(x) вогнутая на промежутке [2; +∞).

(2;–1) – точка перегиба.

№3. Найти вертикальные асимптоты линии:

1. y=tgx;

2. .

Решение.

1. Так как данная функция имеет разрыв в точках x=, то,.

Следовательно, ,– вертикальные асимптоты.

2. Функция имеет бесконечный предел прих2 и х-2.

Значит, прямые х=2 и х= -2 (АВ и А′В′ на рис. 3.6.2) – асимптоты. Прямая АВ служит асимптотой для двух ветвей, UV и KL. Вдоль первой бесконечное удаление направлено вверх, вдоль второй – вниз (ибо и. Аналогично для прямой А′В′.

Заметим, что прямая х=0 служит горизонтальной асимптотой (для ветвей UV и U′V′).

№4. Исследовать функцию и построить ее график.

Решение.

1. Находим область определения функции: (–; –1)  (–1; 1)  (1; ).

2. Точки пересечения с осью ОХ: у=0, тогда

,

х=0, => (0; 0) – точка пересечения с осью ОХ.

Точки пересечения с осью ОУ: х=0, тогда

,

у=0, => (0; 0) – точка пересечения с осью ОУ.

3. Область определения симметрична относительно нуля

Таким образом, функция является нечетной.

4. Так как точки х = 1, х = –1 являются точками разрыва, то вычислим следующие пределы:

Значит х = 1, х = –1 – вертикальные асимптоты.

Теперь найдем наклонные асимптоты.

Итого, уравнение наклонной асимптоты – y = x.

5. Находим критические точки.

Найдем производную функции

Критические точки: x = 0; x = –; x = ; x = –1; x = 1.

Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.

x < –, y > 0, функция возрастает

–< x < –1, y < 0, функция убывает

–1 < x < 0, y < 0, функция убывает

0 < x < 1, y < 0, функция убывает

1 < x < , y < 0, функция убывает

< x, y > 0, функция возрастает

Видно, что точка х = – является точкой максимума, а точка х = является точкой минимума. Значения функции в этих точках равны соответственно: – и .

6. Найдем вторую производную функции

.

Определим выпуклость и вогнутость кривой на промежутках.

x < –1, y < 0, кривая выпуклая

–1 < x < 0, y > 0, кривая вогнутая

0 < x < 1, y < 0, кривая выпуклая

1 < x, y > 0, кривая вогнутая

–1, 0, 1 – точки перегиба.

7. Построим график функции:

Рис. 3.8

.

8. Область значения E(y)=R.