8.2. Уравнение плоской одномерной волны

Составим уравнение, которое позволит находить смещение всякой точки волны в любой момент времени. Пусть в точке В рис.8.2 находится источник колебаний. Волны со скоростью v распространяются от источника колебаний вдоль прямой.

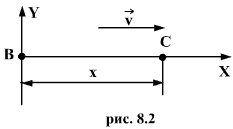
Уравнение колебаний точки В задано в виде:

Все точки вправо от В, например точка С, повторяют колебания точки В с некоторым запозданием. Напишем уравнение колебаний точки С. Если точка В колеблется в течении времени t, то колебания дойдут до точки С по истечении времени  , поэтому время колебаний точки С будет меньше t и составит  . Тогда уравнение колебаний точки С запишется:

Расстояние от точки В до точки С, равное х, волна проходит со скоростью  , откуда  . С учетом  уравнение волны будет иметь вид:

	(8.2)

где λ - длина волны

Обозначим  эта величина называется волновым числом. Тогда получим следующее уравнение

(8.3)

которое называется уравнением плоской одномерной волны и определяет смещение любой точки среды, находящейся на расстоянии х от излучателя в данный момент. Величина

называется фазой волны.

8.3. Фазовая скорость

Зафиксируем какое-либо значение фазы, стоящей в уравнении (2.2), положив ее постоянной для данной точки

Это выражение дает связь между временем t и координатой х, в которой зафиксированное значение фазы осуществляется в данный момент. Определив  , мы найдем скорость, с которой перемещается данное значение фазы. Дифференцируя это соотношение, получим

Откуда

Таким образом, скорость распространения волны V в уравнении (2.2) есть скорость перемещения фазы, в связи с чем ее называют фазовой скоростью.

8.4.Волновая поверхность, фронт волны

Геометрическое место точек, колеблющихся в одной фазе, называется волновой поверхностью. Волновая поверхность, отделяющая часть пространства, в которой колебания происходят, от той части, где еще нет колебаний, называется фронтом волны. Именно фронт волны перемещается со скоростью равной фазовой скорости волны. В случае одномерной синусоидальной волны уравнение волновой поверхности имеет следующий вид:

Этому условию в каждый момент времени удовлетворяет только одна точка оси ОХ, координата х которой равна:

Различным значениям фазы волны φ соответствуют различные волновые поверхности, каждая из которых в одномерных волнах вырождается в точку. Из последней формулы видно, что волновые поверхности с течением времени перемещаются в среде со скоростью, равной , т.е. фазовой скоростью, которая равна

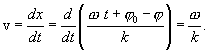
Таким образом, для синусоидальной волны скорость распостранения поверхности постоянной фазы совпадает со скоростью распространения волны.

8.5. Уравнение плоской волны распространяющейся в произвольном направлении

Получим уравнение плоской волны, распространяющейся в направлении, образующем с осями координат х, у, z углы α,β, γ Пусть колебания в плоскости, проходящей через начало координат, имеют вид  .

Возьмем волновую поверхность (плоскость), отстоящую от начала координат на расстоянии l. Колебания в этой плоскости будут отставать от колебаний в точке О (рис.8.3) на время  тогда уравнение волны

(8.4)

Выразим расстояние l через радиус-вектор  точек рассматриваемой поверхности. Для этого введем единичный вектор  нормали к волновой поверхности. Скалярное произведение

Подставим значение l в уравнение (8.4) и внесем в скобки

Отношение  равно волновому числу k. Вектор  равный по модулю волновому числу  и имеющий направление вдоль нормали к волновой поверхности называется волновым вектором. Введя вектор  , получим

(8.5)

Чтобы перейти от радиуса - вектора точки к ее координатам х, у, z , выразим скалярное произведение  через проекции векторов на координатные оси :

Тогда уравнение плоской волны принимает вид:

(8.6)

где