§2.4 Уравнения шредингера. Простейшие случаи движения микрочастиц

ЗАДАЧА №2.34 Почему электрон в потенциальной яме не может иметь непрерывное значение энергии?

Ответ. Электрон – частица – волна имеет неопределенность по координатам. Эта неопределенность равна ширине потенциальной ямы. Электрон неделим и может иметь только такие энергии, при которых соответствующие волны целочисленно (одна, две, три и т.д.) умещаются в потенциальной яме. Это можно сравнить с образованием стоячих волн (основной и обертонов) в струне, зажатой с обоих концов.

ЗАДАЧА №2.35 Больше или меньше энергия частицы, находящейся в «потенциальной яме» с бесконечно высокими «стенками», в состоянии с n=3 по сравнению с состоянием n = 1? Во сколько раз?

Ответ. Собственное значение энергии E_n частицы, находящейся на n-м энергетическом уровне в бесконечно глубоком одномерном прямоугольном «потенциальном ящике» выражается формулой (1.45)

Тогда _.

В состоянии с n = 3 энергия больше чем в состоянии с n = 1 в 9 раз.

ЗАДАЧА №2.36 Электрон в бесконечно глубокой потенциальной яме имеет строго определенную энергию (Е₁ , Е₂ ,… Е_n ), значит и определено значение квадрата импульса электрона р² = 2mЕ. Не противоречит ли это принципу неопределенностей?

Ответ. Не противоречит, т.к. определен только квадрат импульса электрона, а направление импульса не определено (р), что соответствует волне, бегущей и отраженной от стенок потенциальной ямы.

ЗАДАЧА №2.37 Известно, что частица находится в данном объеме. Чему равна вероятность нахождения частицы в этом объеме?

Ответ: .

ЗАДАЧА №2.38 Чему равна разность энергий между четвертым и вторым энергетическими уровнями квантового осциллятора?

Ответ: .

ЗАДАЧА №2.39 Что общего и в чем различие движения частицы: 1) в одномерной бесконечно глубокой потенциальной яме и 2) линейного гармонического осциллятора?

Ответ. В обоих случаях частица движется в одномерной потенциальной яме, но в первом случае потенциальная яма имеет прямоугольную форму, а во втором – параболическую. В результате получается, что при n = 0, в случае прямоугольной ямы и волновая функция и энергия частицы обращаются в нуль, т.е. такой частицы нет. Гармонический же осциллятор при n = 0 имеет нулевую энергию

.

В прямоугольной яме энергия пропорциональна n² и с увеличением n расстояние между уровнями возрастает. У гармонического осциллятора энергия пропорциональна n и энергетические уровни равноотстоящие.

ЗАДАЧА №2.39 Определить энергию электрона, находящегося в бесконечно глубокой прямоугольной потенциальной яме размером 10^-10 м, и найти собственные волновые функции. Представить ответ в графическом виде.

Дано: l = 10∙10 ^–10 м;

Найти: ψ₁ (l) - ? ψ₂ (l) - ? ψ₃ (l) - ?

Решение

U = ∞ за пределами потенциальной ямы для x<0, x>l.

U = 0 внутри потенциальной ямы, для 0  x  l.

Определим граничные условия. Электрон не может находиться в стенках ямы, т. е. волновая функция ψ (0) = 0; ψ (l) = 0.

На рис.10 дано графическое представление заданной потенциальной ямы.

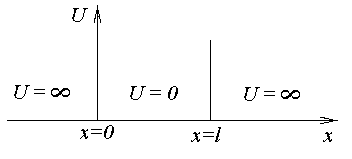
Рис. 10. Бесконечно глубокая прямоугольная потенциальная яма

Запишем основной закон квантовой механики к электрону в потенциальной яме (уравнение Шредингера)

. (2.52)

Это дифференциальное уравнение второго порядка, решением его является волновая функция

(2.53)

Нам неизвестны в этом уравнении ψ₀, Е, φ. Используем для их определения граничные условия. Подставим х = 0 и l = 0

а) ;ψ₀ ≠ 0, следовательно, ,φ = 0.

б) ;_.

В этом случае аргумент , или.

Отсюда определим собственные значения энергии электрона, находящегося на n – ом энергетическом уровне в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками»

(2.54)

где n = 1, 2, 3,…; h=2πħ.

Подставим в (2.54) числовые значения, получим

Е_n = 0,6∙10^{- 17} n ² Дж.

Е₁ = 0,6∙10^-17Дж; Е₂=2,4∙10^-17Дж; Е₃=5,4∙10^-17Дж; Е₄=9,6∙10^-17 Дж.

Изобразим графически энергетический уровни электрона Е₁, Е₂, Е₃, … в потенциальной яме (рис.11).

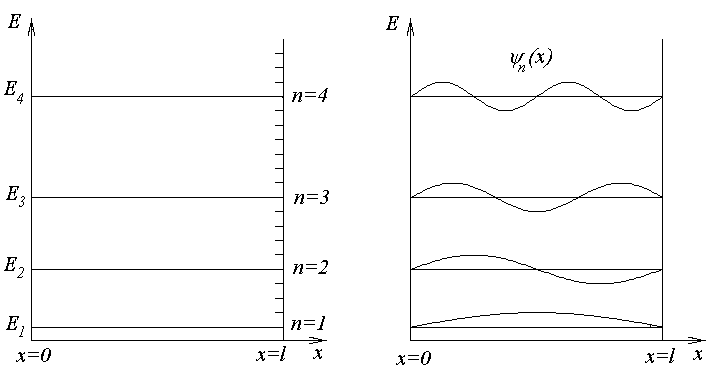
Рис. 11. Энергетические Рис. 12. Собственные

уровни электрона в потенциальной волновые функции для

яме. электрона, находящегося на определенном энергетическом

уровне.

Определим ψ₀ из условия нормировки . Вероятность нахождения электрона в потенциальной ямеР =1.

Подставим в подинтегральное выражение квадрат модуля волновой функции , вынесем за знак интеграла, получим

, а интеграл .

Следовательно, , или.

Итак, волновая функция для электрона в потенциальной яме запишется

, (2.55)

где n =1, 2, 3, …- квантовое число, определяющее состояние электрона в потенциальной яме.