
- •Федеральное агентство по образованию рф
- •Федеральное агентство по образованию рф
- •Часть I. Общие теоретические сведения курса «основы квантовой механики, атомной и ядерной физики».
- •§1.1. Тепловое излучение. Квантовая природа излучения
- •Формула Планка
- •§1.2. Фотоэффект. Давление света
- •Энергия, масса и импульс фотона. Давление света.
- •§1.3 Двойственная природа электромагнитного излучения вещества
- •Корпускулярно – волновая двойственность свойств света
- •Соотношение неопределенностей Гейзенберга
- •§1.4 Уравнения шредингера. Простейшие случаи движения микрочастиц
- •Условие нормировки вероятностей и самой ψ - функции
- •Уравнение Шредингера
- •В случае, когда -функция не зависит от времени , она удовлетворяетстационарному уравнению Шредингера
- •Одномерное уравнение Шредингера для стационарных состояний
- •Движение свободной частицы
- •Частица в одномерной потенциальной яме бесконечной глубины
- •§1.5 Квантово - механическое описание атома и молекул
- •Принцип Паули
- •Уровни энергии двухатомных молекул
- •§1.6 Физика твердого тела
- •Некоторые сведения о квантовой физике твердых тел
- •Распределение Ферми – Дирака имеет вид
- •Теплоемкость кристаллов по Дебаю
- •Понятие о фононах.
- •§1.7 Ядерная физика
- •Активностью а нуклида (общее название атомных ядер, отличающихся числом протонов z и нейтронов n) в радиоактивном источнике называется число распадов, происходящих с ядрами образца в 1с
- •Условие равновесия изотопов в радиоактивном семействе
- •Часть II. Примеры решения задач
- •§2.1. Тепловое излучение. Квантовая природа излучения
- •Решение
- •Решение Энергия с единицы площади поверхности в единицу времени
- •Решение
- •Решение Вычислим энергию фотона по формуле
- •§2.2. Фотоэффект. Давление света
- •Решение
- •Подстановка числовых значений даёт
- •Решение
- •Решение
- •При комптоновском рассеянии длина волны меняется на величину
- •Импульс выразим через длину волны де Бройля
- •1) Определим неопределенность скорости пылинки. Согласно принципу неопределенностей
- •Подставим в (2.51) числовые значения и найдем значение скорости пылинки
- •§2.4 Уравнения шредингера. Простейшие случаи движения микрочастиц
- •Ответ: .
- •Решение
- •Подставим в (2.55) числовые значения, получим
- •§2.5 Квантово - механическое описание атома и молекул
- •Решение
- •Решение
- •Кинетическая энергия вращения молекулы водорода определяется по формуле
- •Решение
- •§2.6 Физика твердого тела
- •Решение
- •Решение
- •Решение
- •Решение
- •§2.7 Ядерная физика
- •Решение
- •Решение
- •Решение
- •Решение
- •Часть III. Контрольные вопросы и задачи для самоподготовки
- •§3.1. Тепловое излучение. Квантовая природа излучения
- •§3.2. Фотоэффект. Давление света
- •§3.3 Двойственная природа электромагнитного излучения вещества
- •§3.4 Уравнения шредингера. Простейшие случаи движения микрочастиц
- •§3.5 Квантово - механическое описание атома и молекул
- •§3.6 Физика твердого тела
- •§3.7 Ядерная физика
- •Продолжение таблицы а.1
- •Приложение б
- •Приставки к единицам си
- •Некоторые основные физические постоянные
- •Продолжение таблицы б.2
- •Некоторые характеристики Солнца, Земли и Луны
- •Работа выхода (а) электронов из металлов
- •Длины волн некоторых спектральных линий
- •Шкала электромагнитных излучений
- •Изотопный состав элементов
Одномерное уравнение Шредингера для стационарных состояний
![]() . (1.39)
. (1.39)
Функции
![]() ,
удовлетворяющие уравнению Шредингера
при заданном видеU
= U
(x,
y,
z),
называются собственными
функциями.
Они существуют лишь при определенных
значениях Е,
называемых собственными
значениями энергии.
Совокупность собственных значений
энергии образует энергетический
спектр частицы.
,
удовлетворяющие уравнению Шредингера
при заданном видеU
= U
(x,
y,
z),
называются собственными
функциями.
Они существуют лишь при определенных
значениях Е,
называемых собственными
значениями энергии.
Совокупность собственных значений
энергии образует энергетический
спектр частицы.
Если U
– монотонная функция, представленная
графиком на рис.5, где
![]() на бесконечности, то в областиЕ<0
собственные значения энергии образуют
дискретный
спектр.
Отыскание собственных значений и
собственных функций составляет важнейшую
задачу квантовой механики.
на бесконечности, то в областиЕ<0
собственные значения энергии образуют
дискретный
спектр.
Отыскание собственных значений и
собственных функций составляет важнейшую
задачу квантовой механики.
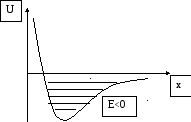
Рис. 5. График зависимости функции U от х.
Движение свободной частицы
При движении свободной частицы (U=0) ее полная энергия совпадает с кинетической. В этом случае одномерное уравнение Шредингера для стационарных состояний примет вид
![]() . (1.40)
. (1.40)
Свободная частица в квантовой механике описывается плоской монохроматической волной де Бройля (1.33) с волновым числом k
![]() . (1.41)
. (1.41)
Выразим из последнего уравнения энергию
![]() . (1.42)
. (1.42)
Зависимость энергии от импульса оказывается обычной для нерелятивистских частиц. Следовательно, энергия свободной частицы может принимать любые значения, т.е. ее энергетический спектр является непрерывным.
Частица в одномерной потенциальной яме бесконечной глубины
Потенциальной
ямой называется
ограниченная область пространства, в
которой потенциальная энергия U
частицы меньше некоторого значения
Umax.
В частности,
при
![]() на обоих концах некоторого промежутка
на оси х имеет место одномерная
потенциальная яма. Это равносильно
тому, что частица ограничена в своем
движении внутри этого промежутка. Если
потенциальная энергия частицы вне и
внутри потенциальной ямы имеют следующие
значения
на обоих концах некоторого промежутка
на оси х имеет место одномерная
потенциальная яма. Это равносильно
тому, что частица ограничена в своем
движении внутри этого промежутка. Если
потенциальная энергия частицы вне и
внутри потенциальной ямы имеют следующие
значения
![]() при
при![]()
![]() при
при![]() и
и![]() , (1.43)
, (1.43)
то яма имеет «плоское дно».
Стационарное уравнение Шредингера для частицы в бесконечно глубокой потенциальной яме имеет вид
![]() . (1.44)
. (1.44)
Собственное значение энергии En частицы, находящейся на n-м энергетическом уровне в бесконечно глубокой одномерно прямоугольной «потенциальной яме»
En
=
![]() (n=1,2,3,…), (1.45)
(n=1,2,3,…), (1.45)
где l - ширина потенциальной ямы; m – масса частицы.
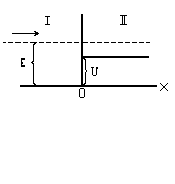
Рис. 6. Низкий потенциальный барьер бесконечной ширины
Соответствующая этой энергии собственная волновая функция
![]() (n=1,2,3…). (1.46)
(n=1,2,3…). (1.46)
Коэффициент преломления n волн де Бройля на границе низкого потенциального барьера бесконечной ширины (рис.6)
![]() (1.47)
(1.47)
где ![]() и
и![]() —
длины волн де Бройля в областях I
и II
(частица движется
из
области I
во II);
k1
и k2
– соответствующие значения волновых
чисел.
—
длины волн де Бройля в областях I
и II
(частица движется
из
области I
во II);
k1
и k2
– соответствующие значения волновых
чисел.
Коэффициенты
отражения
![]() и пропускания
и пропускания
![]() волн де Бройля
через низкий
(U <
E)
потенциальный барьер бесконечной ширины
волн де Бройля
через низкий
(U <
E)
потенциальный барьер бесконечной ширины
![]() ; (1.48)
; (1.48)
![]() , (1.49)
, (1.49)
где k1 и k2 – волновые числа волн де Бройля в областях I и II.
Коэффициент прозрачности D прямоугольного потенциального барьера конечной ширины
D
= D0
exp
![]() (1.50)
(1.50)
где U – высота потенциального барьера, Е – энергия частицы, D0 = 1
(постоянный
множитель, который можно приравнять
единице), d
– ширина
барьера, m
– масса частицы,
![]()
модифицированная постоянная Планка.
модифицированная постоянная Планка.
Из выражения (1.50) следует, что D сильно зависит от массы частицы, ширины барьера и от (U – Е); чем шире барьер, тем меньше вероятность прохождения сквозь него частицы.
Линейный гармонический осциллятор
Линейным (одномерным) гармоническим осциллятором называется частица с массой m, которая колеблется с собственной циклической частотой ω0 вдоль некоторой оси ОХ под действием квазиупругой силы F, пропорциональной отклонению х частицы от положения равновесия:
F=-kx.
Здесь
![]() – коэффициент
квазиупругой силы. Потенциальная энергия
гармонического осциллятора
– коэффициент
квазиупругой силы. Потенциальная энергия
гармонического осциллятора
![]() . (1.51)
. (1.51)
Уравнение Шредингера для линейного гармонического осциллятора
![]() . (1.52)
. (1.52)
Собственные значения энергии гармонического осциллятора
En
= (n
+![]() )
)![]() 0
(n
= 0,1,2…). (1.53)
0
(n
= 0,1,2…). (1.53)
Формула (1.53) показывает, что энергия квантового осциллятора может иметь лишь дискретные значения, т.е. квантуется. Энергия ограничена снизу отличным от нуля, как и для прямоугольной «ямы» с бесконечно высокими «стенками», минимальным значением энергии – энергии нулевых колебаний.
Энергия нулевых колебаний гармонического осциллятора
E0
=
![]()
![]() 0
=
0
=
![]() h0
(при
n=0). (1.54)
h0
(при
n=0). (1.54)
Энергия нулевых колебаний – является типичной для квантовых систем и представляет собой прямое следствие соотношения неопределенностей.
Наличие нулевых колебаний означает, что частица не может находиться на дне «потенциальной ямы», причем этот вывод не зависит от ее формы. Действительно, «падение на дно ямы» связано с обращением в нуль импульса частицы, а вместе с тем и его неопределенности. Тогда неопределенность координаты становится сколь угодно, большой, что противоречит пребыванию частицы в «потенциальной яме».
