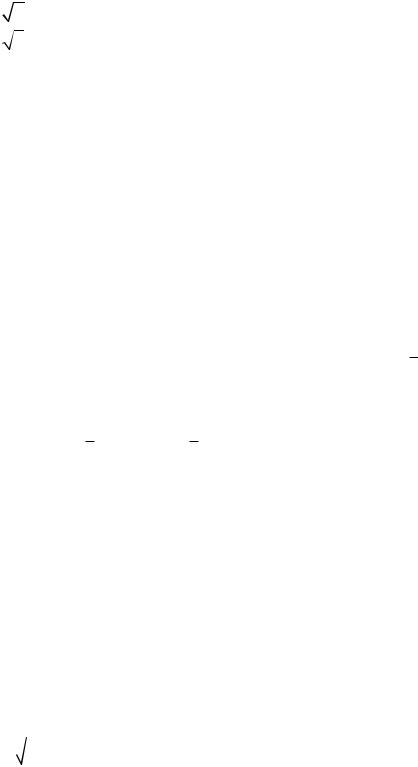Chast_10_TV

Решение:

Найдем P (-0,5 Ј X Ј -0,1) = F(-0,1) - F(-0,5) = F(0,5) - F(0,1). Находим по таблицам эти величины

F(0,1) » 0,0398, F(0,5) » 0,1915. Отсюда

P (-0,5 Ј X Ј -0,1) = 0,1517 .

Найдем P (1 Ј X Ј 2) = F(2) - F(1) » 0,4772 - 0,3413 » 0,1359.

Первая величина больше. Ответ: Первая величина больше

№ 21.

Найдите вероятность того, что случайная величина X отлича ется от своего среднего значения по абсолютной величине не больше, чем на e .

Решение:

Воспользуемся формулой

			ж e ц
P (	X - m	< e) = 2Fз			ч .
При e = s			и s ш
			P = 0,68268,
при e = 2s			P = 0,95450,
при e = 3s			P = 0,99730.

Таким образом, случайная величина X c нормальным распре делением практически не принимает значений, которые отли чались бы по абсолютной величине от среднего больше, чем на 3s , в соответствии с правилом «трех сигм».

№ 22.

Измеряемая случайная величина X подчиняется закону рас пределения N (10;5) . Найдите симметричный относительно mX интервал, в который с вероятностью P попадает измерен ное значение. Рассмотрите следующие числовые значения:

a) P = 0,9974 , б) P = 0,9544 , в) P = 0,50.

Решение:

a) при P = 0,9974 e = 3s = 15 , Ю	X О(-5;25).
б) при P = 0,9544 e = 2s = 10 , Ю	X О(-0;10).
в) при P = 0,50 .

151

ж

µ ц

ж

µ ц

P (

X -10

< µ) = 2Fз

ч = 0,5.

Следовательно,

Fз

ч

= 0,25. По та

и s ш

µ

и s ш

» 0,67 и при

µ» 3,35.

блицам функции F(x) находим s

s = 5

Вычисляем границы интервала 10

- µ» 6,65,

10 + µ» 13,35.

X О(6,65;13,35).

Ответ: (6,65; 13,35)

№ 23.

Измерение дальности до объекта сопровождается системати ческими и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности. Случайные ошиб ки подчинены нормальному закону с s =100 м. Найдите веро

ятность измерения дальности с ошибкой, не превосходящей по абсолютной величине 150 м и вероятность того, что изме ренная дальность не превзойдет истинной.

Решение:

Х — суммарная ошибка измерения дальности.

f (x) =					1			e-(		2s2)		=	1		e-(		1002 )		.
									x-m			2					x+150	2
	(			s	2p					(		100		2p		)		(		)	( )		.
						)
P		X	Ј150				= P				-150		Ј X	Ј150			= F		2		- F 1	= 0,82
		Вероятность того, что измеренная дальность не превзойдет ис
тинной, равна
P (-Ґ Ј X Ј 0) = F(0,5) - F(Ґ) = 0,691.
Ответ: 0,691

8. Предельные теоремы теории вероятностей

8.1. Закон больших чисел

№ 1

Монета бросается 1000 раз. Оцените сверху вероятность откло нения частоты появления герба от вероятности появления гер ба меньше, чем на 0,1.

Решение:

n = 1000, p = q = 12, µ= 0,1; D (X ) = pqn .

152

ж		m		1		ц		D(X )		39	.
P з			-			< µч	і 1-		=
	1000			2				2		40
и						ш		µ
Ответ: і				3940

№ 2

В урне 1000 белых и 2000 черных шаров. Вынули с возвраще нием в урну 3000 шаров. Оцените снизу вероятность того, что число m извлеченных при этом белых шаров удовлетворяет двойному неравенству 80 < m <120 .

Решение:

Перепишем двойное неравенство в виде

80 < m <120 Ю - 20 < m -100 < 20, -																		1	<	m		- 1	<		1
																	15			300				15
																						3
Нужно оценить вероятность неравенства																						m	-	1				<		1	, m =	1	.
																						300		3					15			15
ж		m		1		1		ц		1	Ч	2			5
			-		<				і 1-	3		3		=		.
P з								ч
		300		3		15						1			6
и								ш		300	Ч
												225

Ответ: і 56

№ 3

Дана случайная величина X с математическим ожиданием m и дисперсией s2 . Оцените вероятность того, что величина X от клонится от своего математического ожидания более чем на 3σ.

Решение:

Полагая в неравенстве Чебышева

P ( X - m і a) Ј aD2

a = 3s , имеем P ( X - m і 3s) Ј 9Ds2 = 19 , т. е. вероятность того, что

отклонение случайной величины от ее математического ожи дания не выйдет за пределы 3s , не может быть больше 1/9.

Ответ: Ј 19

153

№ 4

Дана случайная величина X с математическим ожиданием m и дис персией s2 . Оцените вероятность того, что величина X отклонится

от своего математического ожидания менее чем на 31σ.

			Решение:			1
	P (		X - m		< 31s) і 1-		= 0,968.
						2
	0,968					31

№ 5

Случайная величина Xk с одинаковой вероятностью может принимать одно из двух значений: k± и -k± . Определите, удов летворяет ли последовательность X1, X2,...Xk ,... попарно неза висимых случайных величин закону больших чисел:

м		1	n	1	n		< µэ	= 1 ,	µ> 0	, если
lim P н			еXi -		еM (Xi )
п							ь
n®Ґ п		n i=1		n i=1			ю
о

± = -1,8 и ± = 0,42 .

Решение:

Случайные величины попарно независимы. Проверим, являет ся ли дисперсия Xk ограниченной величиной. Составим законы распределения случайной величины Xk для различных a.

	Xk	k-1,8	-k-1,8
	pi	1	1
		2	2

1) ± = -1,8 .

	X 2	k-3,6	k-3,6
	k
	pi	1	1
		2	2

M (Xk ) = 12 (k-1,8 - k-1,8 ) = 0

D (Xk ) = 12 (k-3,6 + k-3,6 ) = k-3,6 = k13,6 Ј 1,

154

D (Xk ) ® 0 при k ® Ґ.

Дисперсия ограничена. Теорема Чебышева выполняется, Xk удовлетворяет закону больших чисел.

2) Проверьте самостоятельно, что при ± = 0,42 закон больших чисел не выполняется. Почему?

8.2. Центральная предельная теорема

№ 6

На отрезке й0, 3 щ случайным образом выбраны п чисел, точнее

к 2 ъ л ы

рассматриваются п независимых случайных величин X1, X2,...Xn , равномерно распределенных на этом отрезке. Определите ве

роятность того, что их сумма заключена между x1

и x2 , то есть

ж

n

ц

P з x1 <

еXi

< x2 ч .

и

i=1

ш

Решение:

3 .

Для равномерного распределения Xi

на отрезке [a,b]

, a = 0, b =

M (Xi )

= a + b = b

=

3

2 ,

2

2

4

D (Xi ) = (b - a)2 = b2 =

3

,

sx = Dx =

b

=

3

.

2

3

4

12

12

16

n

(Xi ) = n b = n 3

. Преобразуем двойное неравенство для

еM

i=1

2

4

искомой вероятности к виду ЦПТ:

ж

<

n

ц

=

P

ж

-

bn

n

ж

b

ц

bn ц

=

P з x1

еXi

< x2 ч

з x1

2

< ез Xi -

2

ч < x2 -

ч

и

i=1

ш

и

i =1

и

ш

2 ш

ж

- bn

n ж

3 ц

x2

- bn

ц

ж

- bn

ц

ж

- bn

ц

з x1

ез Xi -

ч

ч

з x2

ч

з x1

ч

= P з

2

<

i=1 и

4 ш

<

2

ч =

= Fз

2

ч - Fз

2

ч

b n

s

n

b n

b n

b n

з

ч

з

ч

з

ч

з

2

2

ч

з

2

ч

з

2

ч

3

3

3

3

и

ш

и

ш

и

ш

Пусть n = 162 , x1 = 132, x2 = 156 , тогда

155

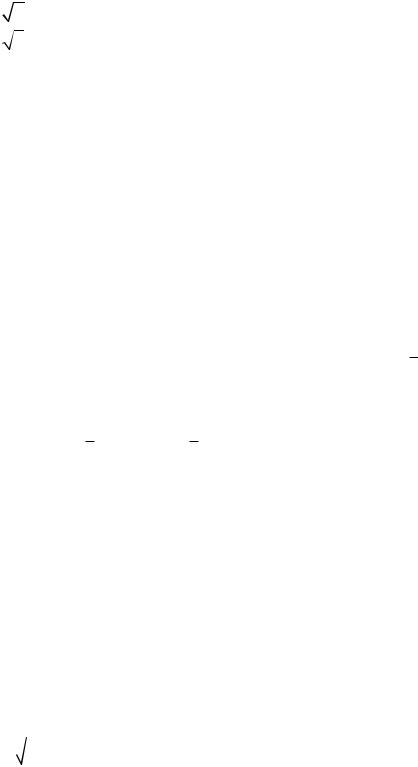
b n			x		- bn		x - bn
		» 11,		2	2	» 6,27 ,	1	2	» 1,9 .
2	3				11			11

По таблице найдем F(6,27) » 0,5, F(1,9) = 0,4712 .

Р = 0,0288. Ответ: 0,0288

№ 7

Складываются 103 чисел, каждое из которых округлено с точно стью до 10–3. Предполагая, что ошибки от округления независи

мы и равномерно распределены в интервале (-0,5Ч10-3; 0,5Ч10-3 ), найти интервал, симметричный относительно математическо го ожидания, в котором с вероятностью 0,998 заключена сум марная ошибка.

Решение:

Представим наблюдавшиеся числа в виде Xi = Xi + Di , где Xi — наблюдавшееся значение, Xi — округленное значение, Di — ошибка округления i -го числа. Очевидно, сумма равна

1000	1000	1000		1000
е Xi = е		(X	i + Di ) = е X				+ SD . Первое слагаемое —
					i + еDi = SX
i =1	i =1		i =1		i =1

сумма округленных значений — неслучайно. Второе — сумма

случайных величин Di , равномерно распределенных на интер

вале

(-0,5Ч10-3;0,5Ч10-3 ) .

Для слагаемых

M (Di ) = 0 ,

1

1000

D (Di ) =

Ч10-6 . Для SD = еDi

соответствующие характеристики:

12

ж1000

ц

i=1

1000

M (SD)

= M

з е Di ч

= е M (Di ) = 0 ,

и

i=1

ш

i=1

ж1000

ц

1000

10-3

,

D (SD) = D з

е Di ч = е D (Di ) =

12

и

i=1

ш

i=1

Ã= D (SD) » 9,13Ч10-3 .

Считая (в соответствии с ЦПТ), что величина SD

распределе

на по закону

s

(

)

( ) , по таблицам функции Лапласа

N

0;1

Ф

x

находим решение уравнения Ф (x) = 0,499 : x = 3,09 , что дает SDs О(-3,09;3,09) , SDО(-0,0282;0,0282) .

156

9. ДОМАШНИЕ ЗАДАНИЯ

ДЗ 1. Случайные события

Гмурман В. Е. Руководство к решению задач по теории вероятно стей и математической статистике: учеб. пособие для студентов вузов / В. Е. Гмурман.  — 9 е изд., стер.  — М.: Высш. шк., 2004.  — 404 с.: ил.

	Задача	Ответ
	1.1. Классическое определение вероятности
1	Монета брошена два раза. Найти вероятность			3
Г7	того, что хотя бы один раз появится «герб».			4
	В коробке шесть одинаковых, занумерованных
2	кубиков. Наудачу по одному извлекают все ку						1
	бики. Найти вероятность того, что номера извле	P =
Г8
	ченных кубиков появятся в возрастающем по				720
	рядке.
	В пачке 20 перфокарт, помеченных номерами
3	101, 102, …, 120 и произвольно расположенных.			12				1
	Перфораторщица наудачу извлекает две карты.	P =					=
Г10
	Найти вероятность того, что извлечены перфо		C20					190
	карты с номерами 101 и 120.
	В ящике имеется 15 деталей, среди которых 10
4	окрашенных. Сборщик наудачу извлекает три	P =		C	3			24
Г12	детали. Найти вероятность того, что извлечен			103				91
	ные детали окажутся окрашенными.			C
				15

157

В конверте среди 100 фотокарточек находится

5

одна разыскиваемая. Из конверта наудачу извле

9

Г13

чены 10 карточек. Найти вероятность того, что

P =

C99

0,1

10

среди них окажется нужная.

C

100

В ящике 100 деталей, из них 10 бракованных.

C 4

90

а)P =

6

Наудачу извлечены четыре детали. Найти веро

C1004

ятность того, что среди извлеченных деталей:

Г14

а) нет бракованных;

C 4

б) нет годных.

б)P =

10

»

C 4

100

» 0,00005

Набирая номер телефона, абонент забыл послед

7

ние три цифры и, помня лишь, что эти цифры

1

1

Г16

различны, набрал их наудачу. Найти вероятность

P =

=

A3

720

того, что набраны нужные цифры.

10

В цехе работают шесть мужчин и четыре женщи

P = C43C64

8

ны. По табельным номерам наудачу отобраны

=

Г18

семь человек. Найти вероятность того, что среди

7

отобранных лиц окажется три женщины.

C10

= 0,5

В группе 12 студентов, среди которых 8 отлични

P = C85C44

9

ков. По списку наудачу отобраны 10 студентов.

=

Г20

Найти вероятность того, что среди отобранных

C129

студентов пять отличников.

= 14

55

1.2. Геометрические вероятности

10

Г26

На отрезке L длины 20 см помещен меньший
отрезок l длины 10 см. Найти вероятность того,
что точка, наудачу поставленная на больший	0,5
отрезок, попадет также и на меньший отрезок.
Предполагается, что вероятность попадания точ
ки на отрезок пропорциональна длине отрезка
и не зависит от его расположения.

158

	В круг радиуса R помещен меньший круг радиу
11	са r . Найти вероятность того, что точка, наудачу
	брошенная в большой круг, попадет также и в ма			P =		r		2
Г28	лый круг. Предполагается, что вероятность по
						R			2
	падания точки в круг пропорциональна площади
	круга и не зависит от его расположения.
	На плоскость,		разграфленную параллельными
	прямыми, отстоящими друг от друга на расстоя
12	нии 6 см, наудачу брошен круг радиуса 1 см. Найти			2
	вероятность того, что круг не пересечет ни одной
Г31	из прямых. Предполагается, что вероятность по			P = 3
	падания точки на отрезок пропорциональна дли
	не отрезка и не зависит от его расположения.
	На плоскости начерчены две концентрические
	окружности, радиусы которых 5 и 10 см соответ
	ственно. Найти вероятность того, что точка, бро
13	шенная наудачу в большой круг, попадет также
	и в кольцо, образованное построенными окруж			0,75
Г32
	ностями. Предполагается, что вероятность попа
	дания точки в плоскую фигуру пропорциональна
	площади этой фигуры и не зависит от ее располо
	жения.
	На отрезке OA длины L числовой оси Ox науда
	чу поставлены две точки: B (x) и C ( y) . Найти ве
	роятность того, что длина отрезка BC окажется
14	меньше, чем	L	. Предполагается, что вероятность	0,75
Г38		2
	попадания точки на отрезок пропорциональна
	длине отрезка и не зависит от его расположения
	на числовой оси.
	Задача Бюффона (французский естествоиспы
	татель XVIII в.). Плоскость разграфлена парал
15	лельными прямыми, отстоящими друг от друга				2l
Г39	на расстоянии 2a. На плоскость наудачу бросают
					pa
	иглу длиной 2l		(l < a) . Найти вероятность того,
	что игла пересечет какую-нибудь прямую.

159

	Задача о встрече. Два студента условились встре
	титься в определенном месте между 12 и 13 часами
16	дня. Пришедший первым ждет второго в течение		7
	0,25 часа, после чего уходит. Найти вероятность
Г42
	того, что встреча состоится, если каждый студент	16
	наудачу выбирает момент своего прихода (в про
	межутке от 12 до 13 часов).

1.3.Теоремы сложения и умножения вероятностей

Вящике 10 деталей, из которых

17	4 окрашены. Сборщик наудачу взял три детали.					P = 1- C63				=
Г47	Найти вероятность того, что хотя бы одна из взя							C103
	тых деталей окрашена.					=	5
							6
	Два стрелка стреляют по мишени. Вероятность
18	попадания в мишень при одном выстреле для
	первого стрелка равна			0,7	, а для второго она рав		0,38
Г51
	на 0,8. Найти вероятность того, что при одном
	залпе в мишень попадет только один из стрелков.
	Вероятность того, что при одном измерении не
	которой физической величины будет допущена
19	ошибка, превышающая заданную точность, рав
	на	0,4	. Произведены три независимых измере				0,432
Г54
	ния. Найти вероятность того, что только в одном
	из них допущенная ошибка превысит заданную
	точность.
20	Студент знает 20 из 25 вопросов программы.							57
	Найти вероятность того, что студент знает пред
Г69
	ложенные ему экзаменатором три вопроса.						115

1.3. Вероятность появления хотя бы одного события

21

Г82

Для разрушения моста достаточно попадания
одной авиационной бомбы. Найти вероятность
того, что мост будет разрушен, если на него сбро	0,5
сить четыре бомбы, вероятности попадания ко
торых соответственно равны 0,3; 0,4 ; 0,6 ; 0,7 .

160