Chast_10_TV

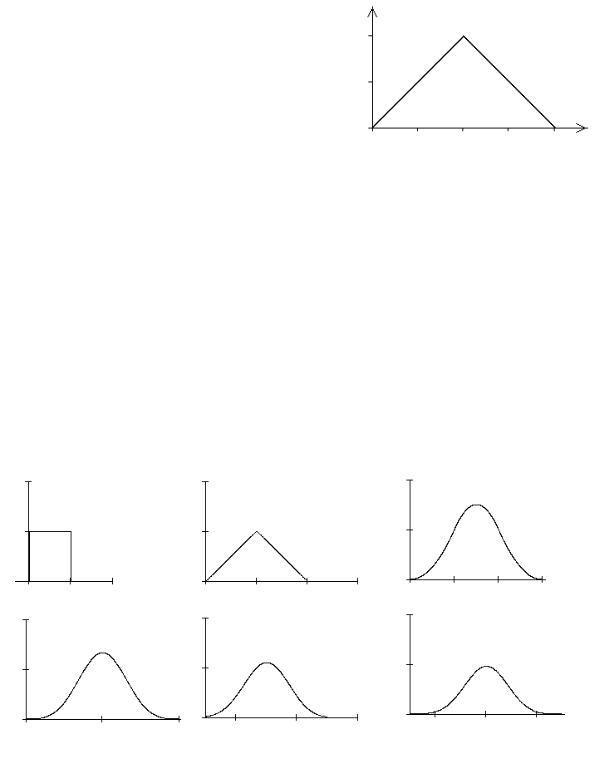
делы единичного отрезка, т. е. при x < 0 , x >1, z - x < 0 , z - x >1. На рисунке показана область на плоскости OXZ , в которой подынтегральное выражение отлично от ноля (и равно 1). Интеграл свертки

придется разбить на два: по отрезку

z О

[

] и по отрезку

[

].

0,1

z О

1,2

z

fX +Y (z )

zЈ0 = 0 , fX +Y (z)

0<zЈ1 = тdx = x

0z = z , 1f

0

fX+Y(z)

fX +Y (z)

1

1z -1 = 2 - z ,

0,5

1<zЈ2 = т dx = x

z -1

0

z

fX +Y (z )

= 0.

0,5

1

1,5

2

z>2

Окончательно получаем тот же результат, что и при геометриче-

	м0,
	п
ском подходе: fX +Y (z) =	пz,
	н
	п2 - z,
	п
	о0,

z Ј 0,

0 < z Ј1,

0 < z Ј1, z > 2.

Рассмотрим суммы равномерно распределенных величин, состоящие из большего количества слагаемых. На рисунках приведе-

ны исходная плотность fX1 (x) и плотности сумм двух fX1 +X 2													(x) , трех
fX1	+X 2 +X3 (x) , четырех fX1 +X 2					+X3 +X 4	(x) , шести			fX1 +X 2 +X3 +X 4 +X5 +X 6 (x)				и вось-
ми		fX1 +X 2 +X3 +X 4 +X5 +X 6 +X 7 +X8			(x)	слагаемых.
2				2						1		fX1+ X2 + X3 (x)
		fX1 (x)				fX1+ X2 (x)
1				1
	0		x 2							0		1
		1			0	1	x	2	3	1		x 2		3
1		fX1+ X2 + X3 + X4		1		fX1+ X2 + X3 + X4 + X5 + X6 (x)					fX1+ X2 + X3 + X4 + X5 + X6 + X7 + X8 (x)
				(x)
0,5				0,5						0,5
	0		2	4	0	2		4	6	0	2	4		6
			x				x					x

Можно заметить, что по мере роста числа слагаемых закон распределения суммы приближается к нормальному закону.

61

Рассмотрим, как влияет суммирование на случайные величины с другими законами распределения.

Пример: Найти плотность распределения суммы двух независимых случайных величин X1 и X2 , распределенных по стандартному

нормальному закону N (0,1) , для которого fX (x) =

Решение: Плотность распределения

	м0,	x < 0,
fX (x) = fY (x) =	п	0 Ј x Ј1,
	н1,
	п	x >1.
	о0,

1 - x2

2p e 2 .

для слагаемых

Используем формулу свертки:

fX1 +X 2 (x

1Ґ

=2p -тҐ e

)

Ґ

(u)Ч fX (x - u)du =

1

Ґ

-

u2

Чe-

(x -u)2

= т fX

т e

2

2 du =

2p

-Ґ

-Ґ

ж

x

2

ц

x2

Ґ

ж

x

ц

2

x2

й

Ґ

-зu2

-ux+

ч

1

1

1

з

2

ч

-

т e

-зu

-

2

ч

-

т e

и

шdu =

e

4

и

ш

du =

e

4

к

2p

-Ґ

2

p

л

p -Ґ

щ

-v2 dvъ .

ы

Интеграл в квадратных скобках равен единице, так как под знаком интеграла стоит плотность нормального распределения

ж

1

ц

(x) =

1

-

x2

0,

. Окончательно получаем fX1 +X 2

4 , т. е., сумма

N з

ч

e

2

2

p

и

ш

двух независимых случайных величин, распределенных по стандартному нормальному закону N (0,1) , распределена по нормаль-

ному закону N (0, 2 ) .

Если сумма двух независимых случайных величин, распределенных по одинаковому закону (возможно, с разными параметрами) имеет такое же распределение, говорят, что это распределение устойчиво относительно суммирования.

Равномерное распределение не устойчиво относительно суммирования, а нормальное устойчиво.

62

7. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

7.1 Закон больших чисел

(предельные теоремы теории вероятностей)

На практике часто рассматривают случайные величины, являющиеся, в свою очередь, суммами большого числа случайных величин. Вычисления непосредственно вероятностей распределения представляют собой определенные трудности. Однако при очень большом числе случайных явлений средний их результат практически не является случайным и может быть предсказан с большой степенью определенности. Например, если в каждом опыте случайная величина X принимает некоторое значение, то при возрастании n®¥ среднее арифметическое наблюдаемых значений случайной величины X становится устойчивым (сходится) к математическому ожиданию случайной величины X. Условия, при которых совокупный результат воздействия случайных факторов практически перестает быть случайным, описываются в нескольких теоремах, которые носят общее название закона больших чисел.

Лемма. Пусть случайная величина неотрицательна, X і 0 , тогда

P(X і e) Ј M(X ) . e

Доказательство: Рассмотрим случай непрерывной случайной величины. Ее плотность распределения, т. к. X і 0 , имеет вид:

м0, x < 0, f (x) = н

о f (x), x і 0.

63

		P(X і e ) = Ґт f (x)dx Ј Ґт			x	f (x)dx + тe		x	f (x)dx =
					e			e
		e		e			0
1	Ґ	1	Ґ			M (X )				M(X )
e	тxf (x)dx = e		т	xf (x)dx =		e	, P(X і e) Ј			e	.
	0		-Ґ

7.1.1. Неравенство Чебышева

Вероятность того, что отклонение случайной величины X от ее математического ожидания (среднего значения) по абсолютной ве-

личине меньше положительного числа

e

, не меньше, чем

1 - D(X )

:

e2

P (

X - mx

< e) і 1 - D(X2

) .

e

Часто

используется

другая

форма

высказывания:

P (

X - mx

і e) Ј D(X2

) .

e

Доказательство:

Применим результат леммы к величине X - mx :

P( X - mx і e) = P((X - mx )2 і e2 ) =

2

M(Y )

M((X - mx )2 )

D(X )

,

P(Y і e

) Ј

=

=

e2

e2

e2

P (

X - mx

< e)

+ P (

X - mx

і e) = 1 Ю P (

X - mx

< e) і 1 - D(X2

) , что

e

и требовалось доказать.

Пример: Оценить сверху вероятность того, что случайная величина X отклонится от своего среднего не меньше, чем на 3sx.

Решение: Используя неравенство Чебышева, получаем

	X - mx		і 3sx ) Ј	sx	2		=	1	, т. е., иными словами, вероятность
P(
				(3sx )		2		9

того, что случайная величина X отклонится от своего среднего больше, чем на 3sx , не превышает 19 .

Для любой случайной величины вероятность невыполнения «правила трех сигма» не превышает 19 . Это справедливо для слу-

64

чайных величин с любым законом распределения. Для большинства случайных величин, встречающихся на практике, ошибка «правила трех сигма» существенно меньше.

Рассмотрим примеры на применение неравенства Чебышева при e = 3sx и сравним точное значение P {x - mx і 3sx } с его верх-

ней оценкой 19 .

Пример: Случайная величина X распределена по показательному закону с плотностью f (x ) = le-lx , x > 0.

Характеристики распределения mx = sx = 1l . Т. к. mx - 3sx , то от-

клонение X от mx больше, чем на 3sx , возможно только в большую сторону.

Таким образом,

P{X > mx + 3sx

м

1

+

3 ь

м

4

ь

ж 4

ц

=

} = P нX >

l

э

= P нX >

l

э

= 1- F з

ч

о

l ю

о

ю

и l

ш

(функция распределения

ц

F (x) = 1 - e-lx )

ж

- l4

= e -4 » 0,0183 ,

что

значительно

= 1- з1- e

l

ч

и

ш

меньше, чем 19 » 0,1111.

Показательное распределение — неблагоприятное для применения «правила трех сигм»: почти 2  % значений с. в. X выходят за

пределы mx + 3sx .

Пример: С.в. X распределена по нормальному закону с параметрами m и s. Вероятность того, что с. в. X попадет в интервал [a;b]:

ж b - m ц

ж a - m ц

1 x

-

t

P{a < X < b} = Ф з

ч

-Ф з

ч

, где Ф (x) =

e 2 dt —

s

s

2p т0

и

ш

и

ш

функция Лапласа.

Вычислим вероятность выполнения «правила трех сигма.

P{ x - m > 3s } = 1- P{ x - m < 3s } = 1- P{m - 3s < X < m + 3s} = 1- 2Ф (3)

Ф (3) » 0,49865.

65

Таким образом,		{	}				, т.е.
	P		x - m	> 3s » 1	- 2Ч0,49865	= 0,0027
ничтожная доля значений с. в. (< 0,3  %) выходит за пределы

интервала m ± 3sx .

Для большинства с. в., встречающихся на практике, «правило трех сигм» выполняется с довольно высокой точностью.

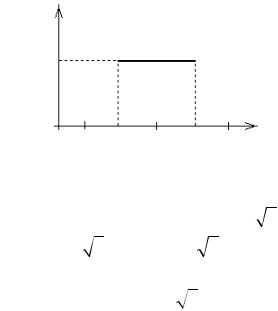
Пример: С.в. X распределена равномерно на отрезке [a;b] . Най-

дем вероятность того, что в результате опыта она отклонится от своего среднего больше, чем на 3sx .

f(x)

Среднее значение mx = b + a , дли-

ны отрезков [a;mx ] и

2

[mx ;b] равны

1

b - a

, равномерно распределенная по

b – a

2

отрезку [a;b] случайная величина не

m – 3σ

a m

b

m + 3σ

может отклониться от среднего значе-

0

x

b + a

больше, чем на

b - a .

ния

2

2

sx

= b - a ; 3sx =

3(b - a)

=

3 (b - a)

.

2

3

2

3

2

Так как

(b - a) <

3 (b - a)

, P (

X - mx

> 3sx ) = 0 .

2

2

7.1.2. Теорема Чебышева

Как видно из примеров, неравенство Чебышева дает весьма грубую оценку вероятностей отклонений с. в., однако оно оказывается весьма полезным при доказательстве различных форм закона больших чисел, так как оно справедливо для любой случайной величины. Перейдем к конкретным формулировкам закона больших чисел. Для независимых с. в. справедлива следующая теорема (Че-

бышева).

Если случайные величины X1, X2,..., Xn,... 1) попарно незави-

симы и 2) их дисперсии ограничены, D (Xi ) ЈC , то как бы мало ни

было положительное число e ,

lim P

м

1

n

X

- 1

n

M

X

< eь = 1

п

е

е

(

i )

.

n®Ґ

н

i

э

п

n i=1

n i=1

ю

о

66

Иными словами, среднее арифметическое значений независимых случайных величин X1, X2,..., Xn,... по мере роста числа слагаемых все меньше отклоняется от среднего арифметического их математических ожиданий.

Доказательство:

ж

1

n

ц

1

n

1

C

Из условий 1), 2) следует D з

еXi ч

=

еD (Xi ) Ј

nC =

.

2

2

Рассмотрим:

и n i=1

ш

n

i=1

n

n

ж	1	n	1	n
P з		еXi -		еmxi
и	n i=1		n i=1
ж	1	n	1	n
1 - P з		еXi -		еmxi
и	n i=1		n i=1

ц	=
< e ч
ш
				n
ц		D(	1 еXi			C
	і 1 -		n i=1		і 1 -			.
і e ч
			e	2		ne	2
ш

Устремим n∞, при этом nCe2 ® 0 , следовательно,

P

ж

1

е

X

- 1

е

m

< e

ц

ѕѕѕ®1

.

з

n

i

n

xi

ч

n®Ґ

и

ш

Следствие: Если X1, X2, …, Xn — попарно независимые случайные величины, имеющие одно и то же математическое ожидание a, и дисперсии этих величин ограничены, то

м		1	n			ь
lim н			еi =1	Xi - a		< eэ =1.
n®Ґ о		n				ю

Таким образом, сущностью теоремы Чебышева является тот факт, что хотя отдельные случайные величины могут иметь значительный разброс относительно своих математических ожиданий, их среднее арифметическое рассеяно мало.

7.1.3. Теорема Маркова

Закон больших чисел может быть распространен и на зависимые случайные величины. Его формулировка для этих условий содержится в следующей теореме (Маркова).

Теорема. Если X1, X2,…, Xn — зависимые случайные величины и если при n ® Ґ

67

D кйеXi ъщ
n
n2	ы	n®Ґ	, то среднее арифметическое наблюденных
л i=1		ѕѕѕ®0

значений с.в. X1, X2,…, Xn сходится по вероятности к среднему значению их математических ожиданий,

P ж

1 n

X

i

-

1 n M

(

X

i )

< e

ц ѕѕѕ®1

.

з

е

е

ч

n®Ґ

и

n i=1

n i=1

ш

1

n

Доказательство: Рассмотрим случайную величину Y =

еXi ;

=

1

ж n

ц

n

i=1

D Y

D

X

ее дисперсия

2

i ч .

( )

n

з е

и i=1

ш

Применим

к

величине Y

неравенство Чебышева:

( )

P (

Y - my

і e) Ј

D Y

.

e

2

Так как по условию D (Y )ѕѕѕ®0 , то при достаточно большом n

n®Ґ

P (Y - my і e) Ј d , или, для противоположного события,

		ж			n		n
		з			еXi		еmxi
P (	Y - my	< e) = P з			i=1	-	i=1
		з			n		n
		з
		и

ц

ч

< e чч > 1 - d , ч. т. д.

ч

ш

7.1.4. Теорема Бернулли

Связь между относительной частотой события и его вероятностью дает следующая теорема (Бернулли).

Теорема: Пусть m — число успехов события А в n независимых испытаниях; p = P (A) — вероятность появления события А в однократном испытании, тогда при стремлении числа испытаний n∞ частота события А сходится по вероятности к вероятности события А,

P	ж		m	- p		< e	ц	ѕѕѕ®1	для любого e >0.
	з		n				ч	n®Ґ
	и						ш

68

7.2. Центральная предельная теорема

Рассмотренные формулировки закона больших чисел утверждали, что некоторые случайные величины сходятся по вероятности к определенным постоянным. Другая группа предельных теорем —

центральная предельная теорема (ЦПТ) — устанавливает вид предельной функции распределения некоторой случайной величины, одновременно оговаривая условия применимости. Приведем вначале простейший вариант ЦПТ.

Теорема: Пусть случайные величины X1, X2,..., Xn,... независимы, имеют одинаковое распределение, конечные математические ожидания M (Xi ) = a и дисперсии D (Xi ) = s2 . Распределение стандартной (т. е. центрированной и нормированной) суммы этих вели-

чин Sn при			n∞					стремится к стандартному нормальному:
	n	ж	n		ц			n
	еXi - M з		еXi ч					еXi	- na	,
Sn =	i=1	и i=1			ш		=	i=1
	ж	n		ц				s	n
	D з	еXi ч
	и i=1			ш
				1			x	t2
	FN (x,0,1)		=			-тҐ e- 2 dt .
				2p

Этот факт выражают и иным способом: если задана последовательность независимых с. в. X1, X2,..., Xn,... с одинаковыми математическими ожиданиями и дисперсиями, то последовательность частичных сумм этой последовательности асимптотически нормальна.

Утверждение ЦПТ о сходимости функции распределения части частичных сумм справедливо и при более широких предположениях. Одно из обобщений, не требующее одинаковости слагаемых, —

теорема Ляпунова.
Теорема: Пусть — X1, X	2,..., Xn,... независимые случайные вели-
чины с математическими ожиданиями m1 = M (X1 ) , m2						,…,		mn ,…
и дисперсиями D1 = D(X1 ) , D2 …, Dn ,… Закон распределения сум-
n
мы Yn = еXi неограниченно приближается к нормальному с мате-
i =1		еMi			еDi
матическим ожиданием M =		i		и дисперсией D =	i			, если
			n			n

69

n
еbk
k=1
м n	3
	ь2
неDk	э
оk=1	ю

ѕѕѕ®0 , где bk = n3 (Xk ) = M

n®Ґ

ный центральный момент величины

( Xk - mk 3 ) — третий абсолют-

Xk .

1). Для нормального закона плотность и функция распределе-

						1		e-	( x -a)2
ния имеют вид:		f (x) =							2s2 ,
						2ps
x	1		x	-	( x -a)2
F (x) = т f (x)dx =			т e		2s2 dx .
-Ґ	2ps -Ґ

2). Если для нормального закона a = 0 , распределение называют нормированным, если s = 0 — центрированным. Нормированное и центрированное нормальное распределение называют стандарт-

ным нормальным.

f (x ) = j(x )

1

-

x 2

, F (x) =

1

+Ф (x) =

1

x

-

x2

=

e

2

2

-тҐ e

2 dx , где

2p

2p

Ф (x) =

1

x

-

x2

т0 e

dx — функция Лапласа.

2

2p

7.2.1. Формула Муавра – Лапласа

как частный случай центральной предельной теоремы

Рассмотрим схему испытаний Бернулли: n — опытов, в каждом случае с вероятностью р может появиться событие А. Пусть

Xi	— случайная величина, связанная с появлением события
А (индикатор события А):		м0, A не наступило,	n	—
		Xi = н	Yn = еXi
		о1, A наступило,	i

число появлений события А в n испытаниях. Величина Yn распределена по биномиальному закону; соответствующие веро-

ятности Pn (m) =Cnm pmqn-m ,					m = 0,1,2,...,n. Среднее значение
(	n )	= np	, дисперсия	(	n )	= npq	. Введем стандартную (цен-
M Y				D Y

70