Chast_10_TV

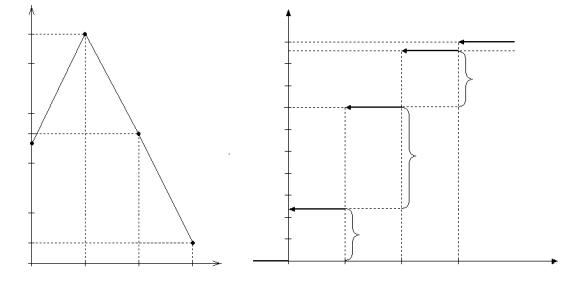
ления. Рассмотрим приведенный ранее ряд распределения с. в. X :

X	0	1	2	3
P	0,24	0,46	0,26	0,04

1.	x Ј 0	F (x) = 0 (т. к. число приборов отрицательным
быть не может);		F (x) = P (X = 0) = 0,24 ;
2.	0 < x Ј1
3.	1 < x Ј 2		(		)	= P	(	X < x	)	= P	(		X = 0		)		+ P		(			)	=
		F		x																	X = 1
= 0,24 + 0,46 = 0,70 ;
4.	2 < x Ј 3		(		)	= P	(	X = 0	)	+ P	(			)		+ P		(		X = 2		)	=
		F		x								X		= 1
= 0,24 + 0,46 + 0,26 = 0,96 ;

5.x > 3 F (x) = P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3) = 1.

Представим ряд распределения и функцию распределения F (x) графически

рi F( )

0,46	0,96	0,04
		0,26

0,7

0,26

0,24

0,46

0,24

0,24

0,04

0

1

2

3

xi

0

1

2

3

4.3. Непрерывная случайная величина. Плотность распределения

С.в. X называется непрерывной, если ее функция распределения является непрерывной и дифференцируемой в любой точке. В качестве закона распределения, имеющего смысл только для непрерыв-

31

ных случайных величин, введем понятие плотности распределения или плотности вероятности. Пусть Dх — бесконечно малый интервал на оси Ох. Вероятность того, что н. с.в. X примет значение, за-

ключенное между х и х+Dх, равна P{x Ј X < x + Dx}. Разделим ее на Dх, получим среднюю плотность вероятности на промежутке (x;x + Dx):

P {x Ј X < x + Dx}.

Dx

Так как

{

}

(

)

(

) , то это выражение

P x Ј X < x

+ Dx

= F

x + Dx

- F

x

можно записать в виде

F (x + Dx) - F (x)

. Переходя к пределу при

Dх→0, получим

Dx

lim F (x + Dx) - F (x)

= F ў(x) .

Dx®0

Dx

Таким образом, плотностью распределения (плотностью вероят-

ности, дифференциальной функцией распределения) н.с.в. Х в точке

х называется производная ее (интегральной) функции распределения в этой точке.

f(x)

f(x)

Обозначение: f (x) = F ў(x) = dxd F (x) .

			График плотности распределения: (x) на-
			зывается кривой распределения.
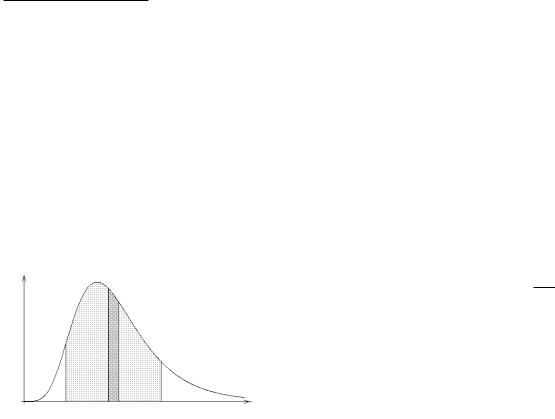
			Рассмотрим элементарный участок
0	α	x x + x β	x dx. Вероятность попадания с. в. Х на
			этот участок dx (с точностью до беско-

нечно малых высших порядков) равна: (x) dx = dF (x). Величина: (х) dx называется элементом вероятности для точки.

Геометрически — это площадь заштрихованной области. Рассмотрим вероятность попадания с. в. Х на участок от a до b. Эта веро-

ятность равна сумме элементов вероятности на этом участке, т. е.

b

определенному интегралу: P{a < X < b} = т f (x)dx .

На рисунке заштрихованная область.a

b

P {a < X < b} = P {X < b}- P {X < a} = F (b) - F (a) = т f (x)dx .

a

Свойства плотности распределения:

1.f (x) ³0;

Ґ

2.т f (x)dx = 1 .

-Ґ

32

м0, при x Ј 0,

пн2x, при 0 < x <1, по0, при x >1

Пример: Функция распределения н. с. в. Х задана выражением

	м0, при x Ј 0,			F(x)
F (x) =	п 2	, при 0	< x <1,	1
	нx
	п1, при x >1
	о			0	1	x

Найти:

1.Плотность распределения f(х) н.с.в. Х и построить ее

график.

2.Найти вероятность того, что с. в. Х в результате опыта

примет значение между 0,25 и 0,5.

Решение 1: f (x) = F '(x) =

f(x)

2

или f(x) = 2x при 0<x<1.

0 0,25 0,5 1 x

Решение 2: Вероятность попадания с. в. Х на участок (0,25;0,5):

0,5

P{0,25 < X < 0,5} = т f (x)dx , но можно воспользоваться формулой:

0,25

P {0,25<X<0,5} = F (0,5) — F (0,25) = 0,2–0,252= 0,1875.

4.4. Числовые характеристики случайных величин

В теории вероятностей числовые характеристики играют огромную роль. С их помощью существенно облегчается решение многих задач.

Чаще всего используются математическое ожидание mx , дис-

n

персия Dx = е(xi - mx )2 pi или среднее квадратическое отклонение

i=1

sx . Они описывают самые важные черты распределения: около како-

го значения группируются значения случайной величины и насколько они рассеяны вокруг этого значения.

4.4.1. Математическое ожидание

Математическое ожидание — характеристика положения, некоторое среднее, ориентировочное значение случайной величины, около которого группируются ее возможные значения. Иногда его называют средним значением случайной величины.

Математическим ожиданием д. с.в. называется сумма произведений всех возможных ее значений на вероятности этих значений.

33

n

M(X ) = еxi pi = mx .

i=1

Пример: Дано распределение случайной величины. Найти М (Х).

X	2	3	4	5
P	0,1	0,2	0,2	0,5

M (X ) = m(x) = 2Ч 0,1+ 3Ч 0,2 + 4 Ч 0,2 + 5Ч 0,5 = 4,1.

При достаточно большом числе опытов можно среднее арифметическое наблюдаемых значений случайной величины принимать приближенно равным ее математическому ожиданию.

Свойства математического ожидания:

1.M (c) = c, с — константа;

2.M (cX ) = cM (X ) ;

3.M (X +Y ) = M (X ) + M (Y ) ;

4.M (X - M (X )) = 0 ;

5.M (X ЧY ) = M (X ) Ч M (Y ) , ( X , Y — независимые с. в.).

Математическим ожиданием н.с.в. Х с плотностью вероятности

Ґ

f(х) называется величина mx = M (X ) = т x Ч f (x)dx .

-Ґ

Пример: Н.с.в. Х распределена на участке (0,2) с плотностью распределения f(x) =ax при xЄ(0,2). Найти коэффициент а и математи-

ческое ожидание mx.			Решение: Построим график ¦ (x), коэффи-
f(x)
		циент			а		найдем		из условия,							что			SD=1.
2		SD	=	1	Ч 2Ч 2a = 1. Следовательно, a =												1 .
				2													2
				2		1		1 2		1 x3				2		8		4
		m	=	x Ч			Ч x Чdx =		x2dx =						=		=		» 1,33.
		x		т		2		2 т		2 3						6		3
0	1	2 x		0				0						0

34

4.4.2. Дисперсия

Характеристикой отклонений с. в. Х от ее математического ожидания является дисперсия, описывающая рассеяние с. в. относительно среднего значения (математического ожидания).

Дисперсией с.в. Х D (x) = Dx называется Dx=M ((X–M5x) 2), где разность X — Mx называется отклонением с.в. Х от ее математического ожидания.

Для непосредственного вычисления дисперсии служат формулы:

	n		— для д.с.в.,
	Dx = е(xi - mx )2 pi
	i=1
	Ґ	2
		(x - mx ) f (x)dx — для н.с.в.
	Dx = т

-Ґ

На практике пользуются формулой: Dx= M (X2) — (M (X)) 2. Она получается из определения:

Dx = M ((X - Mx )2 ) = M (X 2 - 2X Ч Mx + Mx2 ) =

=M (X 2 ) - 2M (X Ч Mx ) + M (Mx2 ) =

=M (X 2 ) - 2Mx Ч Mx + Mx2 = M (X 2 ) - Mx2.

Свойства дисперсии:

1.D(X ) і 0 ;

2.D (c) = 0 ;

3.D (cX ) = c2D (X );

4.D (X +Y ) = D (X ) + D (Y ) , ( X , Y — независимые с. в.);

5.D (X + c) = D (X ).

Пример: В техническом устройстве работают независимо 2 блока. Вероятность безотказной работы первого блока p1= 0,4, второго — p2= 0,7. С.в. Х — число работающих блоков. Найти ее математическое ожидание и дисперсию.

35

Решение: С.в. Х принимает значения 0, 1, 2. Вероятности этих значений: P {X = 0} = 0,6∙0,3 = 0,18; P {X = 1} = 1 — (0,18 + 0,28) = = 0,54; P {X = 2} = 0,4∙0,7 = 0,28.

Ряд распределения случайной величины Х:

X	0	1	2
P	0,18	0,54	0,28

mx = 0∙0,18+1∙0,54+2∙0,28=1,1.

Дисперсия Dx=M (X2) — (M (X)) 2, (M (X)) 2= (1,1) 2=1,21. Найдем M (X2) =02∙0,18+12∙0,54+22∙0,28=1,66.

Dx=1,66–1,21=0,45.

4.4.3. Среднее квадратическое отклонение

Дисперсия имеет размерность квадрата случайной величины. Для наглядности в качестве характеристики рассеивания удобнее пользоваться числом, размерность которого совпадает с размерно-

стью случайной величины.
Величина		Dx = sx	называется средним квадратическим от-
клонением случайной величины (с. к.о.).
3s x	3s x		Если необходимо	узнать диапазон
			возможных значений случайных вели-
			чин, воспользоваться	«правилом трех
	mx		сигм» (доказательство дальше). Это пра-

вило гласит: Значения случайной величины Х с вероятностью, близ-

кой к 1, не выходят за пределы интервала mx ± 3sx .

Для сравнения различных случайных величин бывает удобно привести их к стандартному виду: начало отсчета перенести в точ-

	ку, совпадающую с математическим ожиданием с. в., а масштаб вы-
	брать так, чтобы в новых единицах с. к.о. было равно единице.
	Случайная величина Y = X - MX				называется стандартной слу-
				sx
	чайной величиной, соответствующей случайной величине X .
	ж	X - MX	ц	MX - MX = 0	ж	X - MX	ц	DX
	MY = M з		ч =		, DY = Dз		ч =		= 1.
		sx				sx		2
	и		ш	sx	и		ш	(sx )

4.4.4. Мода, медиана, квантили

Кроме математического ожидания в качестве характеристики положения применяют моду и медиану случайной величины.

Мода д. с.в. — это наиболее вероятное значение с. в.; для н. с.в. — это точка максимума плотности распределения. Обозначение: Мoх.

36

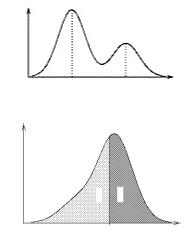
Мода может быть не единственной. Такое f(x) распределение называется полимодальным.

В этом случае часто статистический материал, использованный в исследованиях, является разнородным.

Медиана Мeхс.в. — это такое значение с. в., f(x) для которого P{X < xm}= P{X > xm}= 12 .

Медиана является характеристикой н. с.в. Геометрически медиана — это точка на оси

0x для которой площади под графиком плотности распределения, лежащие слева и справа от

и равны 12 .

Mox Mox x

11

22

Mex

x

нее, одинаковы

Если плотность распределения симметрична относительно прямой x = a и распределение одномодально, то математическое ожидание, медиана и мода совпадают между собой, M (X ) = Mex = Mox .

В приложениях часто используются квантили различных распределений.

Квантилью уровня p qp с.в. X называется решение уравнения F (qp ) = p , где F (x) — функция распределения с. в. X , p — некоторое число, 0 < p <1. Если доля p выражена в процентах, вместо термина «квантиль» используют термин «процентиль», «процентная

точка».

Медиана распределения является квантилью уровня 0,5:

Mex = q0,5 .

4.4.5. Моменты случайных величин

Рассмотренные ранее математическое ожидание и дисперсия с. в. являются частным случаем более общих числовых характеристик — начальных и центральных моментов с. в.

Начальным моментом k-го порядка с.в. X называется число ak (X ) , равное математическому ожиданию k-й степени этой величины, X k :

ak (X ) = M (X k ).

n

Если X — д. с.в., то ak (X ) = еxik pi , где xi — значения, которые

i =1

принимает с.в. X , pi — соответствующие вероятности.

37

Если X — н. с.в., то ak (X )

Ґ

= т xk f (x)dx , где f(х) — плотность

распределения.

-Ґ

Если положить k = 1, то первый начальный момент

1

(

)

n

1

(

)

Ґ

(

)

есть математическое ожидание

=

е i i ,

=

т

a

X

x p

a

X

xf

x dx

i =1

-Ґ

с.в. X , таким образом mx = a1 (X ) .

o

Центрированной случайной величиной X называется отклоне-

o

ние с.в. X от ее математического ожидания: X = X - mx .

Центрирование случайной величины означает перенос начала координат в точку mx .

Центральными моментами с.в. X называются моменты цен-

o

трированной случайной величины X (аналог моментов относительно центра массы в механике).

Центральным моментом порядка k с.в. X называется величина

ж	o	ц	= M ((X - mx )	k	). Если X	n	k
mk (X ) = M з X k ч						— д.с .в., то mk = е(xi - mx ) pi ;
и		ш				i =1

	Ґ	(x - mx )k f (x)dx .
если X — н. с.в., то	ms = т
	-Ґ

Центральный момент 1-го порядка m = M ж Xo ц = M (X - m ) = 0 .

1 з ч x и ш

	ж	o	2	ц	n	2
Второй центральный момент m2					= е(xi - mx )	pi = Dx ,
	= M з X			ч
	и			ш	i=1

т. е. второй центральный момент m2 = M (X 2 )- (M (X ))2 — это дисперсия случайной величины.

Для более детального описания распределения служат моменты

y	высших порядков.
I	II	Центральный момент 3-го поряд-
	ка — m3			выбран в качестве характери-
	стики			асимметрии распределения
	m3	ж	ж	0	ц3 ц
		= M з	з	X	ч	ч , размерность которого
mI mII	x	з	и		ш	ч
		и				ш

38

ex = sm44

x

[X ]3 . Для удобства используют безразмерную величину — коэффи-

циент асимметрии	As = Sk =	m3		(от английского skew — косой).
		3
		s	x

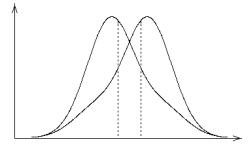
На рисунке имеем две асимметричных кривых распределения. I) — кривая с положительной асимметрией, As > 0 , II) — с отрицательной асимметрией, As < 0 .

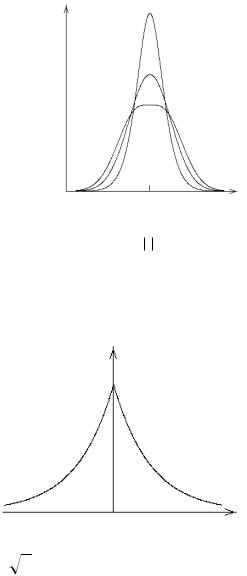
Следующая характеристика, эксцесс, связана с четвертым центральным моментом m4.

- 3.

Число 3 связано с часто встречающимся нормальным распределением, для него

эксцесс ex = 0 ,	m44	= 3.
	s
	x

Для кривых распределения, имеющих более острую вершину, чем нормальные, эксцесс положителен, для более плосковершинных — отрицателен.

Пример: Непрерывная случайная величина Х распределена по закону Лапласа

f(x)

mx

f (x ) = 12 Чe- x .

ε> 0

ε= 0

ε< 0

Найти: математическое ожидание, дисперсию, среднее квадратическое отклонение, асимметрию и эксцесс случайной величины Х.

Решение:

f(x)

Ґ

ж 1

ц

mx = т

-

x

dx = 0 , т. к. интеграл

x з

ч Чe

1

и 2

ш

-Ґ

2

в симметричных пределах от нечетной

функции равен нулю.

Дисперсия:

Ґ

Ґ

Dx = т 12 x2 Чe-

x

dx = 2Ч 12 т x2 Чe- xdx = 2 ;

x

-Ґ

0

среднее квадратическое отклонение sx

=

2 ; коэффициент асимме-

трии Sk= 0, т. к. распределение симметрично относительно матема-

Ґ

1

4

- x

m

4

тического ожидания. Эксцесс: m4 = 2

т0

2

x

Чe

dx = 24 ; ex =

- 3 = 3 .

s4x

39

5. ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ

5.1. Биномиальное распределение

В одной из предыдущих лекций рассматривалась схема повторных испытаний (схема Бернулли) и была получена формула Бернулли, определяющая вероятность появления m успехов в серии из n независимых опытов, в каждом из которых событие А появляется с вероятностью p. Если число успехов рассматривать как с. в. Х, то очевидно, что она может принимать значения 1,2,3,...,n , а соответствующие вероятности даются полученной ранее формулой Бернулли:

	Pn(X = m) =Cnm pm Чqn-m , где q = 1 - p , Cnm =	n!	.
		m!(n - m)!

Данный закон распределения называется биномиальным.

Ряд распределения с. в., подчиняющийся биномиальному закону, имеет вид:

X	0	1	2	…	k	…	n
p	qn	Cn1 pqn-1	Cn2 p2qn-2	…	Cnk pkqn-k	…	pn

Используя формулу бинома Ньютона, можно убедиться, что

n

сумма всех вероятностей равна 1: еCnm pmqn-m = ( p + q)n = 1.

m=0

40