Chast_10_TV

трированную

и

нормированную) случайную величину

Zn =

Y

- np

. Проверим стандартность (M (Zn ) = 0,D(Zn ) = 1) :

nnpq

ж

ц

M Y

n )

- M

(

np

)

M (Zn ) = M зYn - np ч =

(

= np - np = 0

,

з

npq

ч

npq

npq

и

ш

ж

ц

D Y

D (Zn ) = D зYn - np

ч =

( n )

= npq = 1.

з

npq

ч

npq

npq

и

ш

n

В

соответствии

с

центральной

предельной

x

теоремой

n®Ґ

(

), т. е. к нормальному распределению с

и

,

Z

ѕѕѕ®N

0,1

m = 0

s =1

для

которого плотность

распределения равна

функции

Гаусса

f (x )

= j(x )

1

e-

x 2

=

, а функция распределения выражается через

2

2p

функцию Лапласа

F (x) =

1

x

-

x2

1

+Ф (x).

-тҐ e

2 dx =

2

2p

Найдем вероятность того, что в серии из n опытов число успе-

хов m будет лежать между k1 и k2 :

Pn (k1

ж k - np

Ј

m - np

Ј

k

- np ц

Ј m Ј k2 ) = P (k1 - np Ј m - np Ј k2 - np) = P з

1

2

ч .

з

npq

npq

npq

ч

и

ш

События, стоящие в аргументах вероятностей, равносильны, в последнем стоят значения стандартной случайной величины

Zn = Yn - np . Считая, что FZ (x) » FN (x), npq n

ж k - np

Ј

m - np

Ј

k

- np ц

= FZ

ж k

- np ц

-

P з

1

2

ч

з

2

ч

з

npq

npq

npq

ч

n з

npq

ч

и

ш

и

ш

» FN

ж k

- np ц

ж k - np ц

ж k

- np ц

-Ф

з

2

ч

- FN з

1

ч = Ф з

2

ч

з

npq

ч

з

npq

ч

з

ч

и

ш

и

ш

и

npq ш

FZ	ж k - np ц				»
	з	1		ч
	n з		npq	ч
	и			ш

жз k1 - np цч. зи npq чш

т. е. получена интегральная теорема Муавра — Лапласа.

На практике судят о замене биномиального распределения нормальным по выполнению критериев:

np - 3 npq > 0, np + 3 npq < n .

71

Если они выполнены, замена правомерна.

Пример: Станок с ЧПУ делает за смену n =1000 изделий, из которых 2  % дефектов. Найти вероятность того, что за станком будет изготовлено не менее 970 недефектных изделий.

Решение: p = 0,98 — вероятность изготовления доброкачественных изделий, Y — число нормальных изделий, n = 1000;

Проверка

условий:

(

)

= np

= 980

;

s

y

[

]

=

npq = 4.43

,

M Y

= s Y

np - 3sy > 0, np + 3sy <1000 .

Пользоваться можно.

ж

970 - 980

ц

f Y і 970

)

= P

(

970 ЈY < +Ґ

)

= F

Ґ

)

- F

= 0,988

.

(

(

з

4,43

ч

и

ш

72

8. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ

1. Комбинаторная математика

Принцип умножения. Перестановки. Размещения. Сочетания

№ 1

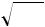
Если из пункта А в пункт В можно добраться пароходом, самолетом, автобусом и поездом, а из пункта В в пункт С пароходом и автобусом, то каким количеством способов можно добраться из пункта А в пункт С?

Решение:

Изобразим все возможные пути проезда и подсчитаем их. Это удобно связать с построением специального графа, который называется деревом.

Исходную точку, или вершину, обозначим через А. Возможные пути из точки А к правой крайней вершине дерева: Существует mЧ n = 4 Ч 2 = 8 способов проезда.

	B n = 4
m = 4
A	или	A	B	C
		m = 4		n = 4

Ответ: 8

№ 2

Колода карт для игры в бридж состоит из 52 карт, которые делятся на четыре равные группы по масти. Карты каждой масти

73

различают по значению. Имеется 13 значений (2, 3, … 10, валет, дама, король, туз). Сколько существует комбинаций (пар) карт?

Решение:

В качестве множеств элементов берутся четыре масти и тринадцать значений соответственно. Таким образом, существует

4 Ч13 = 52 пары.

Ответ: 52

№ 3

В розыгрыше первенства участвует 16 команд.

Каким количеством способов могут быть распределены золотая и серебряная медали?

Решение:

После того как определен владелец золотой медали, серебряную медаль может получить одна из 15 команд. Общее число способов, которыми могут быть распределены золотая и серебряная медали, равно 16Ч15 = 240 .

Ответ: 240

№ 4

Группа людей классифицируется по полу, семейному положению и профессии. Сколько различных классов получится, если имеется 17 профессий?

Решение:

Всего будет 2Ч 2Ч17 = 68 классов.

Ответ: 68

№ 5

Сколько четырехзначных чисел можно составить из цифр {0, 1, 2, 3, 4, 5}, если:

а) ни одна из цифр не повторяется более одного раза; б) цифры могут повторяться; в) числа должны быть нечетными (цифры могут повторяться)?

Решение:

а) Первой цифрой числа может быть одна из пяти цифр {1, 2, 3, 4, 5}. Если первая цифра выбрана, то вторая может быть выбрана пятью способами; третья — четырьмя, четвертая — тремя способами, значит, существует 5Ч5Ч 4 Ч3 = 300 таких чисел.

74

б) Первой цифрой может быть одна из цифр {1, 2, 3, 4, 5} (5 возможностей), для каждой из следующих цифр

имеем 6 возможностей (0, 1, 2, 3, 4, 5), значит, существует 5Ч 6Ч 6Ч 6 = 5Ч 63 = 1080 таких чисел.

в) Первой цифрой может быть одна из пяти {1, 2, 3, 4, 5}, а последней одна из трех {1, 3, 5}, т. к. числа должны быть нечетными. Существует 5Ч 6Ч 6Ч3 = 540 таких чисел.

Ответ: а) 300; б) 1080; в) 540

№ 6

Каким количеством способов можно распределить 5 шаров по 8 ящикам?

Решение:

Размещение r = 5 шаров по n = 8 ящикам равнозначно выбору ящика для каждого шара. Для 5 шаров мы имеем 8 независимых выборов, поэтому r = 5 шаров можно разместить в n = 8

ящиках n Ч n Ч n ... n = nr = 85 различными способами.

r

Ответ: 85

№ 7

Каким количеством способов можно расставить на полке три книги (А, В и С)?

Решение:

а) Изобразим все возможные размещения в виде дерева из точки О и подсчитаем их:

		B	C	ABC
	C	A	B	ACB
			C	BAC
0	B
	C		A	BCA
		A
			B	CAB
	C
			A	CBA
	B

Число способов расстановки книг равно шести. б) Изобразим три места на полке:

На первое место мы можем поместить или А, или В, или С, поэтому первое место мы можем запол-

нить тремя способами, второе — двумя,третье — одним:

75

3

3

2

3

2

1

Общее число способов расстановки находится умножением

3Ч 2Ч1 = 6 .

в) Число способов расставить книги равно числу перестановок множества из трех элементов:

P3 = 3! = 3Ч 2 = 6 .

Ответ: 6

№ 8

Сколько различных четырехзначных чисел можно получить из цифр: 3, 4, 5, 6?

Решение:

Числа отличаются друг от друга только порядком входящих в их написание цифр, их столько, сколько можно составить перестановок из четырех элементов: P4 = 4! = 24.

Ответ: 24

№ 9

Каким количеством способов можно упорядочить множество {1, 2, 3, … 2n} так, чтобы каждое четное число имело четный номер?

Решение:

Число мест с четными номерами равно n. Четные числа можно расставить на них n! способами. При этом по основному принципу комбинаторики мы должны учесть, что если мы упорядочиваем 2n чисел, среди которых n нечетных, это число должно быть умножено на n! способов размещения нечетных чисел на местах с нечетными номерами. Следовательно, существует n!Ч n! = (n!)2 способов таких упорядочений.

Ответ: (n!)2

№ 10

Сколько можно составить перестановок из n элементов, в которых данные 2 элемента не стоят рядом?

Решение:

Имеется n мест. Посчитаем число способов размещения n элементов на этих местах, когда элементы a и b стоят рядом. Число способов размещения элемента b справа от элемента a равно

76

(n-1), так как попарно они могут занять первое-второе, второетретье, …, (n-1) и n места.

Элементы a и b можно поменять местами, следовательно, существует 2(n -1)способа размещения a и b рядом.

Кроме того, по основному принципу комбинаторики нужно учесть, что каждому из этих способов соответствует (n-2)! перестановок других элементов.

Следовательно, число перестановок, в которых a и b стоят рядом, равно:

2(n -1)(n - 2)! = 2(n -1)!

Число всех возможных перестановок равно n!. Искомое число перестановок, в которых a и b не стоят рядом, равно разности:

n! - 2(n -1)! = (n - 2)(n -1)!.

Ответ: (n – 2) · (n – 1)!

№ 11 Каким количеством способов можно рассадить 4 студента на

25 местах?

Решение:

Искомое число способов равно числу размещений из 25 по 4:

A425 = 25Ч24 Ч23Ч22 = 303600 .

Ответ: 303600

№ 12 Студенту нужно сдать 4 экзамена за 8 дней. Каким количеством

способов можно это сделать?

Решение:

а) Искомое число способов равно числу четырехэлементных упорядоченных подмножеств (дни сдачи экзаменов) множества из 8 экзаменов:

A84 = 8Ч7Ч6Ч5 = 1680 .

б) Если последний экзамен нужно сдавать на восьмой день, то число способов равно

4 A73 Ч 4 = 4 Ч7Ч 6Ч5Ч 4 = 840 .

Ответ: а) 1680, б) 840

№ 13 Колода карт для игры в бридж состоит из 52 карт, которые делятся

на четыре равные группы по масти. Карты каждой масти различа-

77

ют по значению. Имеется 13 значений (2, 3, … 10, валет, дама, король, туз). Сколько комбинаций карт может быть у одного игрока при игре в бридж, если порядок карт у игрока не существенен?

Решение:

Число различных комбинаций карт у одного игрока равно

C13	=	52!		= 635013559600 .
52		13!Ч39!

Ответ: 6Ч1011

№ 14

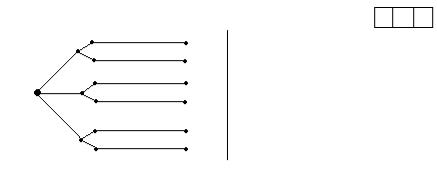
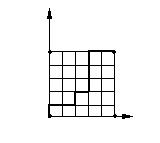
Дана прямоугольная сетка квадратов размером m+n («шахматный город»). Каково число различных кратчайших путей по сторонам ячеек сетки из левого нижнего угла в правый верхний угол?

Решение:

Каждый кратчайший путь из точки (0,0)

		в точку (m, n) состоит из (m+n) отрезков,
	(m, n)	причем среди них есть m горизонтальных
(0, n)		и n вертикальных. Разные пути отличаются
		лишь порядком их чередования. Общее число
(0, 0)	(m, 0)	способов, которыми из m+n отрезков можно
		выбрать n вертикальных, равно Cmn+n =Cmm+n .
		Ответ: Cmn+n

№ 15 Каким количеством способов из команды в 7 человек

а) можно выбрать трех лучших, б) наградить их золотой, серебряной и бронзовой медалями?

Решение:

а) Искомое число способов равно числу трехэлементных подмножеств множества из 7 элементов, т. е. числу сочетаний из семи элементов по три:

C3	=	7!	= 1Ч 2Ч3Ч 4 Ч5Ч 6Ч 7 = 35 .
7		3!Ч 4! 1Ч 2Ч3Ч1Ч 2Ч3Ч 4

б) В этом случае порядок становится существенным и выбирать нужно упорядоченные трехэлементные подмножества, их число равно числу размещений из семи элементов по три:

A73 = 74!! = 5Ч 6Ч 7 = 210.

Ответ: 35, 210

78

№ 16 Сколько шестизначных чисел будет содержать трижды цифру

1, дважды цифру 5 и один раз цифру 9?

Решение:

C6 (3,2,1) = Ч6! Ч = 60 . 3! 2! 1!

Ответ: 60

№ 17 Сколько различных слов можно составить из п букв, если имеется

k1 букв a1, k2 букв a2 … и kr букв ar (k1 + k2+… + kr = n)?

Сколько различных слов можно составить из слова «математика»?

Решение:

Перенумеруем места, на которых стоят буквы, числами 1, 2, … n.

Каждое слово определяется множествами: b1 {номера мест, на которых стоит буква a1}, b2 {номера мест, на которых стоит буква a2} и далее до br. Следовательно, число различных слов равно числу способов, которыми можно множество А = {1,2, … n} разбить на r упорядоченных частей bi (i=1, 2, … r), т. е.

Cn (k1, k2, … kr).

Найдем число различных слов, которое можно составить из слова «математика».

В этом случае

n = 10, k1	(M ) = 2, k2 (A) = 3, k3(T ) = 2, k4 (E) = 1, k5(И ) = 1, k6(К ) = 1,
и число слов равно
C (2,3,2,1,1,1) =		10!	= 151200 .
10	2!3!2!

Ответ: 151200

№ 18 Каково число сочетаний костей домино?

Решение:

Число сочетаний костей домино можно рассматривать как сочетания с повторениями по два из семи цифр: 0, 1, 2, 3, 4, 5, 6.

Число таких сочетаний равно:

D72 = C86 = 6!8!2! = 82Ч 7 =28 .

Ответ: 28

79

№ 19 Каким количеством способов можно выбрать 6 одинаковых

или разных пирожных в кондитерской, где есть 11 разных сортов?

	Решение:		16!		6Ч15	Ч14 Ч13Ч12Ч11	= 8008 .
	D116 = C116 =			=
		6!10!			6	Ч5Ч 4 Ч3Ч 2

Ответ: 8008

2. Случайные события и операции над ними

2.1. Алгебра событий

№ 1

Монета подбрасывается три раза. Наблюдаемый результат — появление герба Г или цифры Ц на верхней стороне монеты. Постройте множество элементарных исходов W опыта и множества элементарных исходов, соответствующих указанным событиям (подмножествам исходного опыта):

А {герб выпал ровно один раз}; B {ни разу не выпала цифра};

C {выпало больше гербов, чем цифр};

D {герб выпал не менее, чем два раза подряд}.

Решение:

W= {ГГГ, ГГЦ, ГЦГ, ГЦЦ, ЦГГ, ЦГЦ, ЦЦГ, ЦЦЦ};

А{ЦЦ, ЦГЦ, ЦЦГ};

В {ГГГ}; С {ГГЦ, ГГГ, ЦГГ, ГЦГ};

D {ГГЦ, ГГГ, ЦГГ}.

№ 2

Какие из событий:

А {попадание в мишень первым выстрелом},

B {попадание в мишень по крайней мере одним из четырех выстрелов},

C {попадание точно в мишень одним из 2 выстрелов}, D {попадание в мишень не более чем 5 выстрелами} являются частью другого события?

Решение:

A МC М B М D

80