Chast_10_TV

Чтобы найти числовые характеристики с. в. X, введем новую с. в.

Xi — индикатор события A (i = 1,2,...,n ). Она может принимать два значения: Xi = 1, если в i-м испытании событие A произошло и Xi = 0 , если событие в i-м опыте не наступило. Исходная с. в.

n

X = еXi . Ряд распределения с. в. Xi

i =1

Xi

0

1

p

q

p

Математическое ожидание M (Xi ) = p .

Дисперсия D (Xi ) = M ((Xi )2 )- (M (Xi ))2 = p - p2 = pq .

n

Найдем характеристики X = еXi , учитывая независимость ве-

личин Xi :

i =1

ж

n

ц

n

,

M (X ) = M з

еXi ч = еM (Xi ) = np

и i=1

ш

i=1

ж

n

ц

n

npq .

D (X ) = D з

еXi ч =

еD (Xi ) = npq , s(X ) =

и i=1

ш

i=1

Найдем математическое ожидание и дисперсию относительной

частоты

появления

события

A:

m

=

X

:

ж

X ц

1

M (X ) = p,

n

n

M з

ч =

n

и

n ш

ж

X ц

1

D (X ) =

npq

pq

ж

X ц

pq

D з

ч =

=

, sз

ч =

.

n

2

n

2

n

n

и

n ш

и

n ш

Полученный результат показывает обоснованность статистического определения вероятности — среднее значение относительной

частоты mn = p — вероятности появления события в однократном

испытании, а дисперсия, т. е, разброс значений вокруг среднего, уменьшается по мере роста n .

5.2. Распределение Пуассона

В пределе при n→∞, р→0, lim(np) = l = const биномиальное рас-

n®Ґ

пределение переходит в распределение Пуассона. Распределение

41

Пуассона можно приближенно применять вместо биномиального, когда число опытов n очень велико, а вероятность p очень мала, т. е.

вкаждом единичном опыте событие А появляется крайне редко.

Всвязи с этим говорят о длинной серии маловероятных событий и закон Пуассона называют законом редких событий.

Случайная величина X, распределенная по закону Пуассона,

принимает значения k = 0,1,2,... с вероятностями P (X = k) = lk e-l . k!

Число l > 0 — параметр распределения, смысл которого будет уточнен при вычислении числовых характеристик распределения.

Убедимся, что сумма всех вероятностей равна 1:

еP (X = k) = 1	:еl	k	e-l = e-l еl	k	=e-lel =1.
Ґ	Ґ		Ґ
k=0	k =0 k!		k =0 k!

Найдем математическое ожидание с. в., распределенной по закону Пуассона.

M (X )	= еk l			k	e
		Ґ
		k=0	k!
Ґ	m
= le-l е l		= le-lel
m=0 m!

Ґlk Ґ lk-1

-l = e-l еk=1 (k -1)! = e-llеk=1 (k -1)! = k -1 = m =

=l .

Таким образом, параметр распределения Пуассона l — среднее количество событий за определенный промежуток

времени (средняя интенсивность потока). Найдем дисперсию:

D (X ) = M (X 2 )- (M (X ))2 = еk2 l

k

e-l

Ґ

k=0

k!

ж

Ґ

(k -1)l

k

+

Ґ

l

k ц

- l2

= e-l

= e-l з

е

е

ч

з

(k -1)!

ч

и k =1

k =1 (k -

1)! ш

=

k -1 = m

= e-l

ж

Ґ

ln

Ґ

lm

ц

k -

2 = n

з l2

е

n!

+ lе

ч - l2

и

n=0

m=0 m!

ш

- l2 = e-l е(k -1+1)l								k		- l2	=
		Ґ		(		)
		k=1
					k -1		!
ж	Ґ	lk		Ґ		lk			ц
з	е		+	е					ч	- l2	=
з		(k - 2)!							ч
и k =2				k =1 (k -1)! ш

= e-l (l2 + l)el - l2 = l ,

дисперсия также равна параметру распределения.

Свойством, что математическое ожидание и дисперсия равны, пользуются при проверке гипотезы, что неизвестная с. в. распределена по закону Пуассона.

42

Если оценки математического ожидания и дисперсии, полученные на основании опытных данных, близки между собой, то есть основания считать, что исследуемая с. в. распределена по закону Пу-

ассона.

Пример: Вероятность попадания в цель при одном выстреле равна 0,01. Какова вероятность того, что после 200 выстрелов цель будет поражена?

Решение: Воспользуемся формулой Пуассона. Событие А = {цель поражена} является сложным (цель поражена одним выстрелом, цель поражена двумя выстрелами и т. д.). Рассмотрим

противоположное событие A = {цель не поражена}, его вероятность легко находится: параметр l = np = 2 ,

0

P (A) = P200 (0) » 2! e-2 » 0,135 . P (A) = 1- P (A) » 0,865.

0

5.3. Равномерное распределение

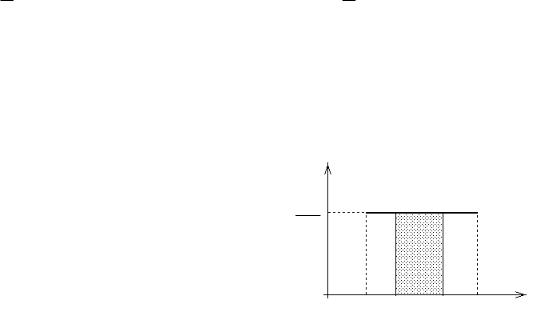
С.в. X распределена равномерно на участке от а до b, если ее

плотность ¦ (х) на этом участке постоянна

	м 0, при x < a, и x > b,
f (x) =	п
	н 1		, при a < x < b.
	п
	оb a
Вероятность попадания с. в. X на
любую часть			участка, например,

участка (a, b) P{a < X < b} = bb --aa .

f(x)

1 b – a

0

a α

β

b

x

Найдем функцию распределения F (x): F (x) = P{X < x} = тx

f (x)dx .

-Ґ

x<a,

¦ (x) =0, F (x) =0.

1

x

1

a

x

1

x - a

, F (x) = т

dx = т 0 Чdx + т

a<x<b,

f (x) =

dx =

.

b - a

b - a

b - a

b - a

-Ґ

-Ґ

a

x>b,

a

b

x

b dx

b - a

F (x) = т f (x)dx + т f (x)dx + т f (x)dx =

т

= b - a

= 1.

b - a

-Ґ

a

b

a

43

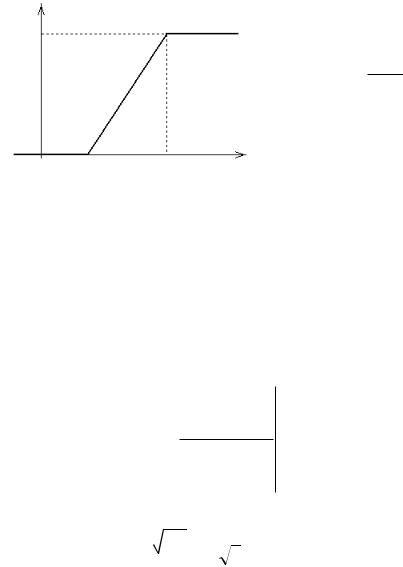
f(x)

0

a

b

x

График функции распределения:

м0, при x < a,

п

F (x) = п x a , при a < x < b,

нпb a

п1, при x>b.

о

Вычислим математическое ожидание с. в. X :

Ґ	b xdx		x2		b	b2 - a2		b + a
mx = т	xf (x)dx = тb - a	=			=		=		. Вычислим дис-
			2(b - a)			2(b - a)		2
-Ґ	a		2		a
	+Ґ
персию с.в. X : Dx = т (x - mx ) f (x)dx

-Ґ

		b	ж	b + a ц2		dx
	=	тa	з x -		ч
				2		b - a
			и		ш

ж - b + a ц3 b з x 2 ч

= и 3(b - a)ш

a

= (b - a)2 . Среднее квадратическое

12

отклонение sx = Dx = b - a .
2	3
Мода y равномерного распределения отсутствует.
Медиана (из соображений симметрии) mx = a + b		= Mex
	2

Из соображений симметрии m3 = 0, коэффициент асимметрии

	Sk=0,		1 b		ж	a + b ц4		(b - a)4
									;
	m4	=			з x -		ч dx =
			b - a тa			2		80
					и		ш

эксцесс ex = ms44 - 3 = -1,2 ; эксцесс отрицателен.

x

Пример: Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в случайный момент времени.

44

f (x)dx .

Найти плотность распределения случайной величины Т — времени, в течение которого ему придется ждать поезда, ее математическое ожидание, дисперсию и среднеквадратическое отклонение.

Решение:

		1				1				2	1	x2			2
f (x) =					=		(0<x<2); mx = т x				2 dx =					= 1,
		2 - 0				2						4
										0					0	f(x)
Dx =	(2 - 0)2		4			=	1	, sx =	3	.						1
		=														2
	12		12				3		3

0

1

2

x

5.4. Показательное распределение

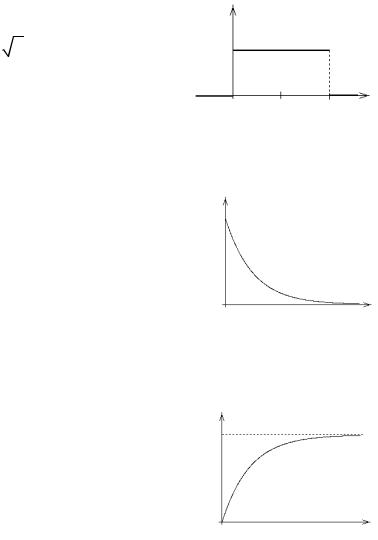
С.в. X имеет показательное (экспоненциальное) распределение, если

мle-lx , x і 0, f (x) = н

о0, x < 0.

l > 0 называется параметром распределения.

Функция распределения F (x): F (x) = тx

-Ґ

f(x)

λ

0

x

x<0, F (x) =0.				0		f(x)
			x		x
x>0, F (x) = т f (x)dx = т					f (x)dx +т f (x)dx =	1
			-Ґ	-Ґ	0
lтx e-lxdx = - ll тx e-lxd(-lx) =						0	x
0			0
-e-lx		x	= -e-lx + e0	= 1 - e-lx .
		0			м1 - e-lx , x > 0,
Таким образом, F (x) =
					н
					о0, x < 0.

Вычислим математическое ожидание показательного распреде-

Ґ	Ґ	Ґ	1
ления mx = т	xf (x)dx = тxle-lxdx = lтxe-lxdx =			;
-Ґ	0	0	l

(для вычисления интеграла интегрируем по частям).

45

Дисперсия:

Ґ

Ґ

2

1 ) le-lxdx =

Dx = т

(x - mx )2 f (x)dx = т(x -

-Ґ

0

l

Ґ

Ґ

x

Ґ

1

= тlx2e-lxdx - т

2

le-lxdx + т

1

le-lx =

.

l

l2

l2

0

0

0

Среднее квадратическое отклонение: sx =

1

, т.е. mx = sx =

1 .

l

l

Вычислим асимметрию показательного распределения, для это-

Ґ

ж

1 ц3

-lx

2

го: m3

=

т0

з x -

ч le

dx =

.

l

3

и

l ш

m3

Коэффициент асимметрии Sk =

= 2 > 0 , что и следовало ожи-

3

s

дать.	x

Показательное распределение связано с простейшим потоком событий. Покажем, что интервал времени Т между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром, равным интенсивности потока.

f (t ) = le -lt , t і 0 .

Найдем функцию распределения F (t) = P (T < t).

t

Чтобы выполнялось неравенство T < t ,

нужно, чтобы хотя бы одно событие потока

0

T

t

попало на участок длиной t. Вероятность

этого события

описывает

пуассоновское

распределение:

Pm =

(lt)m e-lt . Вычислим вероятность противоположного события

m!

;

(

)

, откуда

.

: (m=0) 0

= e-lt

0

= 1- e-lt

F (t) = 1 - e-lt

T і t

P

P T < t

= 1

- P

Дифференцируя, получаем: f (t) = F ў(t) = le-lt — показательное распределение.

5.5. Нормальное распределение (распределение Гаусса)

Нормальное распределение занимает в математике особое положение в силу своей важности.

1 (x-m)2

Плотность распределения: f (x) = s 2p e- 2s2 , где m,s — параметры распределения.

46

s 2p

f(x)

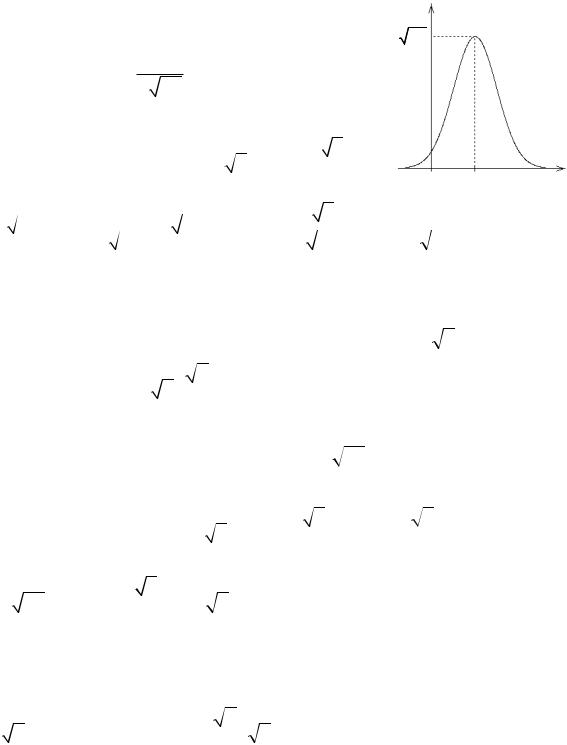
Кривая распределения: максимум достигается при x = m. => Мода Mox= m.

Математическое ожидание:

	Ґ		1
	mx = т	xf (x)dx =
			s 2p
	-Ґ

(замена переменной t

dx = 2sdt ) ... =	1	Ґ (s
	p -тҐ

Ґ		(x-m)2
т xe-		2s2 dx = ...
-Ґ
	x - m
= ( s 2 ) , x = ts 2			+ m ,	0	m	x
2t	+ m)e-t2 dt = s 2 Ґт te-t2 dt +			m	Ґт e-t2 dt = ...
		p -Ґ		p -Ґ

Ґ

( т te-t 2 dt

— равен нулю, как интеграл от нечетной функции

-Ґ

Ґ

Ґ

т e-t 2 dt =

2тe-t 2 dt = p — интеграл

в симметричных пределах;

m

-Ґ

0

Пуассона), mx =

Ч p = m — центр рассеивания с. в. X .

p

Ґ

2

Ґ

1

(x - m)2 e-

(x-m)2

Дисперсия Dx = т (x - mx ) f (x)dx = т

2s2

dx =…

2p

-Ґ

-Ґ s

x - m

(замена переменной t = ( s

2 ) , x = ts 2 + m , dx = 2sdt )

…=

1

Ґт t 2s2 2e-t 2 2sdt =

s2

Ґт 2t 2e-t 2 dt = ...

s 2p -Ґ

p -Ґ

1 e-t 2

(интегрирование по частям: t = u , dt = du , te-t 2 dt = dv ,v = -

),

2

s2

ж

Ґ

Ґ

ц

s2

2

2

... =

з

-te-t

-Ґ

+ т e-t

dt ч =

p Ч

=s2.

p

p

и

-Ґ

ш

e-t 2

при t ® Ґ убывает быстрее, чем любая степень t => -te-t 2

® 0 ;

Dx = s2 .

Таким образом, параметр m для нормально распределенной с. в.

X является ее математическим ожиданием, а параметр s — средним квадратическим отклонением.

47

На

ex = sm44

x

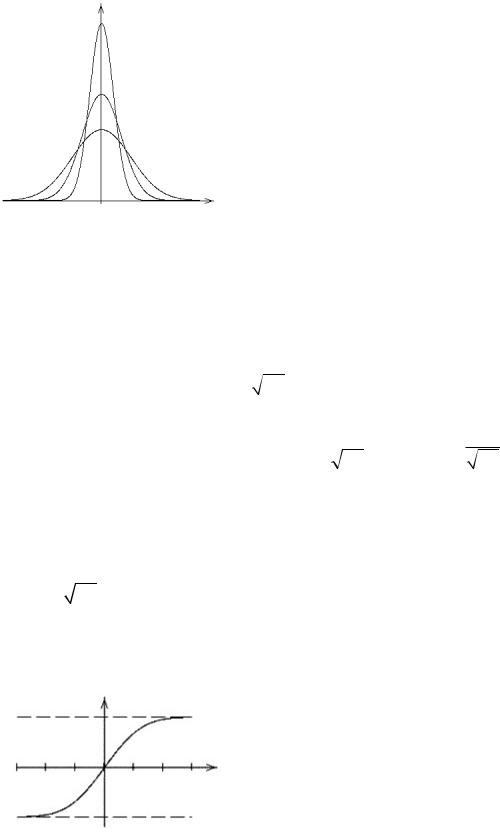
f(x)		Рассмотрим изменение кривой рас-
I		пределения в зависимости от параметров
		распределения. При изменении m кривая
		смещается вдоль оси абсцисс. При увели-
II		чении s кривая распределения становит-
III		ся более плоской, растягивается вдоль оси
		абсцисс, при уменьшении s — вытягива-
0	x	ется вверх, одновременно сжимаясь с бо-
		ков (площадь под кривой всегда равна 1).

рисунке кривая I имеет s=2/3, II — s=1,		III — s=3/2.
- 3 = 0 , т. к. для нормального распределения	m44	= 3.
	s
	x

Вычислим вероятность попадания с. в. X на участок от a до b:

		b	1	b	-	( x-m)2
P(a < X < b) = т f (x)dx =				тe			2s2	dx = ...
		a	s 2p a
									b-m		-t2
(замена t =	x - m	, x=ts+m, dx=sdt) ... =					1		s
									т	e	2 sdt =
	s						s 2p a-m

s

1

2p

b-m

тs

a-m s

-t2

e 2 dt = ...

Последний интеграл не выражается через элементарные функции, но его можно выразить через специальную функцию

1

x

-

t2

Ф(x) =

e

2 dt — функцию Лапласа.

2p

т0

P{a < X

< b} =Ф(b - m) -Ф(a - m) .

s

s

y

Свойства функции Лапласа:

0,5

( )

1)

Ф (0) = 0 ,

–3

–2

–1

0

1

2

3

x

2) Ф (-x) = -Ф (x) (нечетная),

–0,5

3)

Ф (Ґ) = 0,5 .

Рассмотрим функцию распределения F (x):

1

ж

х - m ц

F (x) = P (X < x) = P (-Ґ < X < x) =

a = -Ґ,b = х,Ф(-Ґ) = -0,5

=

+Ф з

ч .

2

s

и

ш

48

В связи с широкой распространенностью нормального распределения для него часто используется специальное обозначение: нормальный закон с математическим ожиданием m и среднеквадратическим отклонением s обозначается N (m,s) .

Закон нормального распределения очень широко распространен в случайных явлениях природы. Он возникает в тех случаях, когда складываются много независимых случайных величин Х1, Х2,..., Хn .

Какими бы ни были законы распределения величин Х1, Х2,..., Хn , закон распределения их суммы будет близок к нормальному.

Примеры нормальных распределений: ошибки «точных измерений», ошибки стрельбы, вызывающие отклонение снарядов от точки прицеливания, ошибки вывода космического корабля в заданную точку пространства и т. п.

49

6. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

6.1. Многомерные случайные величины

На одном и том же пространстве событий может быть определена не одна, а несколько случайных величин. Это возникает в случае, когда изучаемый объект характеризуется несколькими случайными параметрами.

Пример: Составляется модель расходов случайно выбранной семьи на одежду, обувь, питание, транспорт и т. д. Эти затраты являются случайными величинами на одном пространстве элементарных событий.

Пусть Х1, Х2,..., Хn — случайные величины, определенные на множестве элементарных событий W. Для удобства будем рассматривать их как координаты случайного n-мерного вектора Х = (Х1, Х2,..., Хn ) (это упорядоченный набор n случайных величин Х1, Х2, …, Хn).

Система случайных величин есть функция элементарного со-

	бытия (Х1, Х2,..., Хn ) = j(w), т. е. каждому элементарному событию
	w ставятся в соответствие значения случайных величин: Х1, Х2, …,
	Хn, полученных в результате опыта.					или
	Многомерной		случайной		величиной		случай-
	ным вектором			(w) называется совокупность			случай-
		Х
	y	ных величин {X1(w), X2(w),..., Xn(w)} .
		Рассмотрим двумерную случайную величину
	(X, Y) M
		X (w) = {X (w),Y (w)} .
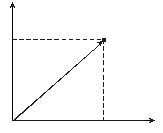
				Геометрическая интерпретация двумерной
		случайной величины — это случайная точка на
		плоскости с координатами (X, Y) или случай-
	0	x ный вектор OM .

50