4.3 Уравнение с разделяющимися переменными

Определение. Уравнением с разделяющимися переменными называется дифференциальное уравнение первого порядка вида

,

где – заданные функции своих переменных.

Метод решения. Разделив обе части уравнения на и почленно взяв квадратуры (проинтегрировав), получим общий интеграл уравнения:

;

.

Замечание. Прямые ибудут интегральными кривыми уравнения с разделяющимися переменными, еслииявляются соответственно корнями уравненийи.

Пример. Решить уравнение

.

Разделим обе части уравнения на и получим общий интеграл уравнения:

;

;

.

Так как прямые иобращают выражениев нуль, то они также будут решениями.

4.4 Однородное уравнение

Определение. Однородным уравнением первого порядка называется дифференциальное уравнение первого порядка вида

.

Метод решения. С помощью подстановки однородное уравнение приводится к уравнению с разделяющимися переменными по отношению к новой неизвестной функции:

.

Беря квадратуры от обеих частей уравнения, получим общий интеграл:

;.

Определив из последнего уравнения функцию , находят общее решение исходного однородного уравнения

Пример. Решить уравнение

.

Используя подстановку , находим общий интеграл:

;

.

4.5 Линейное уравнение

Определение. Линейным уравнением первого порядка называется дифференциальное уравнение первого порядка, линейное относительно неизвестной функции y и ее производной :

,

где p(x) и q(x) – заданные функции.

Метод решения. С помощью подстановки , гдеи– две неизвестные функции, уравнение преобразуется к виду

и сводится к двум уравнениям с разделяющимися переменными относительно каждой из неизвестных функций u и v:

1) ; 2).

Из первого уравнения определяем и, подставляя его во второе уравнение, определяем, после чего находим общее решениеисходного линейного уравнения. При этом при решении первого уравнения полагаем аддитивную постояннуюC равной нулю.

Пример. Решить уравнение

.

Используя подстановку , находим общее решение:

1)

2)

.

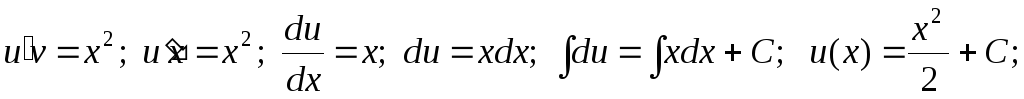
4.6 Уравнение Бернулли

Определение. Уравнением Бернулли называется дифференциальное уравнение первого порядка вида

,

где p(x) и q(x) – заданные функции.

Метод решения. С помощью подстановки , гдеи– две неизвестные функции, уравнение преобразуется к виду

и сводится к двум уравнениям с разделяющимися переменными относительно каждой из неизвестных функций u и v:

1) ; 2).

Из первого уравнения определяем и, подставляя его во второе уравнение, определяем, после чего находим общее решениеисходного уравнения Бернулли. При этом при решении первого уравнения полагаем аддитивную постояннуюC равной нулю.

Пример. Решить уравнение

.

Используя подстановку , находим общее решение:

1)

2)

.

4.7 Дифференциальные уравнения высшего порядка

Определение. Уравнение вида

,

где x – независимая переменная, y – искомая функция, – ее производные, называетсядифференциальным уравнением высшего (n-го) порядка.

Если это уравнение можно разрешить относительно старшей производной , то оно принимает вид

и называется уравнением высшего порядка, разрешенным относительно старшей производной.

В дальнейшем будем рассматривать именно такие уравнения.

Пример. Уравнение высшего (третьего) порядка, разрешенное относительно старшей (третьей) производной:

.

Определение. Общим решением дифференциального уравнения высшего порядка называется семейство функций

,

обращающих дифференциальное уравнение в тождество при любых значениях произвольных постоянных .

Определение. Общим интегралом дифференциального уравнения высшего порядка называется семейство функций

,

обращающих дифференциальное уравнение в тождество при любых значениях произвольных постоянных .

Определение. Частным решением дифференциального уравнения высшего порядка называется любая функция

,

получаемая из общего решения при задании определенных значений всем n произвольным постоянным: .

Определение. Частным интегралом дифференциального уравнения высшего порядка называется любая функция

,

получаемая из общего интеграла при задании определенных значений всем n произвольным постоянным: .

Определение. Условия, что при функцияи ее производные должны равняться заданным числам соответственно, называютсяначальными условиями для дифференциального уравнения высшего (n-го) порядка:

, ,

, ,

, или ,

………….. …………..

, .

Определение. Задача, в которой требуется найти частное решение дифференциального уравнения

,

удовлетворяющее заданным начальным условиям

,

,

,

…………..

,

называется задачей Коши или начальной задачей для дифференциального уравнения высшего (n-го) порядка.

Ответ на вопрос о том, при каких условиях, налагаемых на функцию , задача Коши имеет решение, дает теорема Коши, которая называетсятеоремой существования и единственности решения дифференциального уравнения .

Теорема 4.2 (теорема Коши) (без доказательства). Если в уравнении функцияи ее частные производные первого порядка по аргументамопределены и непрерывны в некоторой области, то, какова бы ни была внутренняя точкаобластиD, в некоторой окрестности этой точки существует единственное решение данного уравнения, удовлетворяющее условиям

,

,

,

…………..

.

Пример. Найти общее решение дифференциального уравнения третьего порядка

и выделить из полученного общего решения частное решение, удовлетворяющее начальным условиям:

.

Последовательно интегрируя почленно исходное уравнение (беря квадратуры), находим общее решение:

,

,

.

Это решение зависит от трех произвольных постоянных . Определим их, подставляя в полученные соотношения начальные условия:

;

;

.

Таким образом, частное решение, удовлетворяющее заданным начальным условиям, имеет вид

.

Наряду с основной начальной задачей часто приходится решать так называемые краевые или граничные задачи. В этих задачах значения искомой функции и/или ее производных задаются не в одной, а в двух точках, ограничивающих отрезок, на котором требуется определить решение. При этом число заданных краевых условий обычно равно порядку дифференциального уравнения. Для каждого класса краевых задач, как и для задачи Коши, требуется решать вопрос о существовании и единственности решения.

Пример. Найти решение дифференциального уравнения , удовлетворяющее на отрезкекраевым условиям:.

Последовательно интегрируя почленно исходное уравнение (беря квадратуры), находим общее решение:

.

Это решение зависит от двух произвольных постоянных C₁ и C₂. Определим их, подставляя в полученные соотношения краевые условия:

;

.

Таким образом, искомое решение, удовлетворяющее заданным краевым условиям, имеет вид

.