
- •Росжелдор
- •6.5 Вычисление тройного интеграла в декартовых координатах …………. 70
- •1 Неопределенный интеграл
- •1.1 Первообразная функция
- •1.2 Неопределенный интеграл
- •1.3 Основные свойства неопределенного интеграла
- •1.4 Таблица основных интегралов
- •1.5 Основные методы интегрирования
- •1.6 Интегрирование рациональных функций
- •1.7 Интегрирование выражений, содержащих тригонометрические функции
- •2.2 Основные свойства определенного интеграла
- •2.3 Производная определенного интеграла по переменному верхнему пределу
- •2.4 Формула Ньютона-Лейбница
- •2.5 Замена переменной в определенном интеграле
- •3.2 Несобственные интегралы второго рода (от неограниченных функций)
- •3.3 Признаки сходимости несобственных интегралов
- •3.4 Абсолютная и условная сходимости
- •4 Обыкновенные дифференциальные уравнения
- •4.1 Общие понятия
- •4.2 Дифференциальные уравнения первого порядка
- •4.3 Уравнение с разделяющимися переменными
- •4.5 Линейное уравнение
- •4.8 Уравнения высшего порядка, допускающие понижение порядка
- •1) Уравнение вида .
- •2) Уравнение вида .
- •3) Уравнение вида .
- •4.9 Линейные дифференциальные уравнения высшего порядка
- •4.10 Линейное однородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
- •1) Найти общее решение однородного дифференциального уравнения .
- •4.11 Линейное неоднородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
- •5 Системы обыкновенных дифференциальных уравнений
- •5.1 Нормальная система дифференциальных уравнений
- •5.2 Интегрирование нормальной системы методом исключения неизвестных
- •5.3 Нормальная система линейных дифференциальных уравнений с постоянными коэффициентами
- •5.4 Понятие устойчивости решения нормальной системы по Ляпунову
- •6 Кратные интегралы
- •6.1 Двойной интеграл
- •6.2 Вычисление двойного интеграла в декартовых координатах
- •6.3 Вычисление двойного интеграла в полярных координатах
- •6.4 Тройной интеграл
- •6.5 Вычисление тройного интеграла в декартовых координатах
- •6.6 Вычисление тройного интеграла в цилиндрических и сферических координатах
- •7 Криволинейные интегралы
- •7.1 Криволинейный интеграл первого рода
- •7.2 Криволинейный интеграл второго рода
- •7.3 Связь между криволинейными интегралами первого и второго рода
- •7.4 Формула Грина
- •8 Поверхностные интегралы
- •8.1 Поверхностный интеграл первого рода
- •8.2 Поверхностный интеграл второго рода
- •8.3 Связь между поверхностными интегралами первого и второго рода
- •8.4 Формула Остроградского
- •8.5 Формула Стокса
- •9 Практические задания
- •9.1 Неопределенные интегралы
- •9.2 Обыкновенные дифференциальные уравнения первого порядка
- •9.3 Обыкновенные дифференциальные уравнения высшего порядка
1.7 Интегрирование выражений, содержащих тригонометрические функции
1)
Интегралы вида:
![]() .
.
Чтобы вычислить эти интегралы, следует представить подынтегральное произведение в виде суммы, используя формулы:
![]() ,
,
![]() ,
,
![]() .
.
Пример![]()

2)
Интегралы вида:
![]() ,
,
где
R
– рациональная функция от тригонометрических
аргументов
![]() и
и![]() .
.
Такие
интегралы сводятся к интегралам от
рациональных функций от «обычных»
аргументов с помощью соответствующих,
в зависимости от вида функции
![]() ,
подстановок:
,
подстановок:
а)![]() –
нечетная функция от
–
нечетная функция от![]() .
.
Подстановка
![]() .
.
б)![]() –
нечетная функция от
–
нечетная функция от![]() .
.
Подстановка
![]() .
.
в)![]() –
четная функция от
–
четная функция от![]() и
и![]() .
.
Подстановка
![]() .
.
г)![]() –
произвольная рациональная функция от
–
произвольная рациональная функция от![]() и
и![]() .
.
Подстановка
![]() (универсальная).
(универсальная).
Пример

1.8 Интегрирование некоторых иррациональных выражений
1)
Интегралы вида
 ,
,
где
R
– рациональная функция своих аргументов;
![]() –
целые числа;
–
целые числа;
![]() –
действительные числа.
–
действительные числа.
Такие интегралы вычисляются с помощью подстановки
![]() ,
,
где s
– общий знаменатель дробей
 .
.
Пример

2) Интегралы вида:
![]() ,
,
где R – рациональная функция своих аргументов.
Такие интегралы вычисляются с помощью соответствующих тригонометрических или гиперболических подстановок:
![]() или
или
![]() – для интеграла
– для интеграла
![]() ;
;
![]() или
или
![]() – для интеграла
– для интеграла
![]() ;
;
![]() или
или
![]() –
для интеграла
–
для интеграла
![]() .
.
Пример
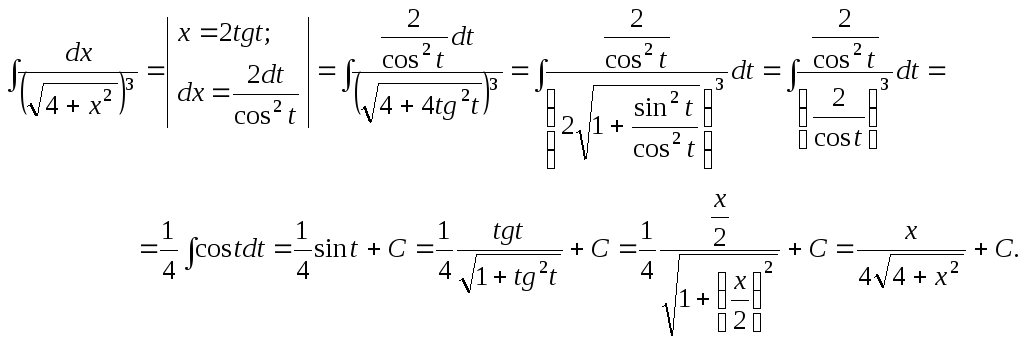 3)
Интегралы вида
3)
Интегралы вида
![]() ,
,
где R – рациональная функция своих аргументов.
Такие интегралы вычисляются с помощью выделения полного квадрата в квадратном трехчлене и последующей заменой переменной
![]() .
.
В результате замены исходный интеграл приводится к одному из интегралов вида 2).
Пример

![]()
![]()
 .
.
2 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2.1 Определение определенного интеграла
Пусть непрерывная
функция
![]() определена на отрезке
определена на отрезке![]() .
Разобьем этот отрезок наn
произвольных
частей точками
.
Разобьем этот отрезок наn
произвольных
частей точками
![]() .
.
В каждом из
полученных частичных
отрезков
![]() выберем произвольную точку
выберем произвольную точку![]() .
Через
.
Через![]() обозначим разность
обозначим разность![]() ,
которую условимся называтьдлиной
частичного отрезка
,
которую условимся называтьдлиной
частичного отрезка
![]() .
.
Образуем сумму
 ,
,
которую назовем
интегральной
суммой для
функции
![]() на отрезке
на отрезке![]() ,
соответствующей данному разбиению
отрезка
,
соответствующей данному разбиению
отрезка![]() на частичные отрезки и данному выбору
промежуточных точек
на частичные отрезки и данному выбору
промежуточных точек![]() .Геометрический
смысл суммы
.Геометрический
смысл суммы
![]() очевиден:
это сумма площадей прямоугольников с
основаниями
очевиден:
это сумма площадей прямоугольников с
основаниями
![]() и высотами
и высотами![]() (если
(если![]() на отрезке
на отрезке![]() )
(рис. 2.1).
)
(рис. 2.1).

Рис. 2.1 Геометрический смысл интегральной суммы и определенного интеграла
Обозначим
через
![]() длину
наибольшего частичного отрезка разбиения:
длину
наибольшего частичного отрезка разбиения:
![]() .
.
Определение.
Определенным
интегралом от
функции
![]() на отрезке
на отрезке![]() называется предел интегральных сумм
при стремлении к нулю длины наибольшего
частичного отрезка разбиения, если этот
предел существует и не зависит ни от
способа разбиения отрезка
называется предел интегральных сумм
при стремлении к нулю длины наибольшего
частичного отрезка разбиения, если этот
предел существует и не зависит ни от
способа разбиения отрезка![]() на частичные отрезки, ни от выбора в
каждом из них точки
на частичные отрезки, ни от выбора в
каждом из них точки![]() :
:
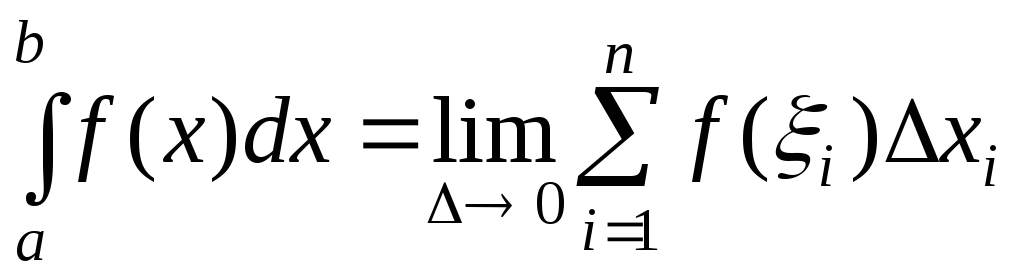 .
.
Функция
![]() называетсяинтегрируемой
на отрезке
называетсяинтегрируемой
на отрезке
![]() .
Числаa
и
b
называются соответственно нижним
и верхним пределами интегрирования,
а отрезок
.
Числаa
и
b
называются соответственно нижним
и верхним пределами интегрирования,
а отрезок
![]() –отрезком
интегрирования.
Функция
–отрезком
интегрирования.
Функция
![]() называется такжеподынтегральной
функцией,
называется такжеподынтегральной
функцией,
![]() –подынтегральным
выражением,
x
– переменной
интегрирования.
–подынтегральным
выражением,
x
– переменной
интегрирования.
Из определения следует, что определенный интеграл представляет собой некоторое число и не зависит от обозначения переменной интегрирования:
 .
.
Из
определения определенного интеграла
и рис. 2.1 следует геометрический
смысл определенного интеграла:
определенный интеграл от неотрицательной
функции
![]() по отрезку
по отрезку![]() численно равен площади криволинейной
трапеции
численно равен площади криволинейной
трапеции![]() ,
т.е. фигуры, ограниченной осьюОх,
графиком функции
,
т.е. фигуры, ограниченной осьюОх,
графиком функции
![]() и двумя прямыми
и двумя прямыми![]() и
и![]() .
.
Теорема 2.1 существования определенного интеграла (без доказательства).
Если
функция
![]() непрерывна на отрезке
непрерывна на отрезке![]() ,
то для нее на этом отрезке существует
определенный интеграл.
,
то для нее на этом отрезке существует
определенный интеграл.
Замечание.
Класс
интегрируемых функций шире, чем класс
непрерывных функций. Например,
интегрируемыми являются также
кусочно-непрерывные на отрезке
![]() функции.
функции.
