3.3 Признаки сходимости несобственных интегралов

Рассмотрим достаточные признаки сходимости несобственных интегралов (признаки сравнения), позволяющие выяснить вопрос о сходимости несобственного интеграла без знания первообразной его подынтегральной функции.

Признак сравнения 1 (без доказательства). Пусть на промежутке функцииинепрерывны и удовлетворяют неравенствам. Тогда:

1) если интеграл сходится, то сходится и интеграл;

2) если интеграл расходится, то расходится и интеграл.

Признак сравнения 2 (без доказательства). Пусть на промежутке функцииинепрерывны и удовлетворяют неравенствам. Тогда, если существует конечный и отличный от нуля предел

,

то несобственные интегралы иоба сходятся или оба расходятся.

Замечание 1. Аналогичные признаки сравнения справедливы и для других видов несобственного интеграла первого рода, а также для несобственных интегралов второго рода.

Замечание 2. При применении признаков сравнения требуется знать несобственные интегралы, относительно которых заранее известно, сходятся они или расходятся. В качестве таких «эталонных» интегралов на практике часто используются следующие несобственные интегралы:

1) несобственный интеграл первого рода

,

который сходится при и расходится при;

2) несобственный интеграл второго рода

,

который сходится при и расходится при.

Пример. Исследуем на сходимость несобственный интеграл первого рода

.

Так как на промежутке

,

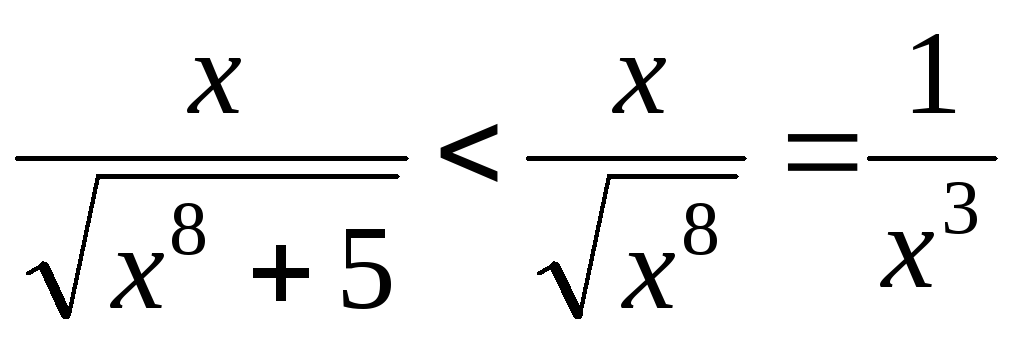а интеграл сходится, то по признаку сравнения 1 исходный интеграл также сходится.

3.4 Абсолютная и условная сходимости

Определение. Несобственный интеграл называется абсолютно сходящимся, если сходится несобственный интеграл от абсолютной величины подынтегральной функции.

Несобственный интеграл называется условно сходящимся, если он сходится, а несобственный интеграл от абсолютной величины подынтегральной функции расходится.

Теорема 3.1 (без доказательства). Абсолютно сходящийся интеграл сходится.

Используя понятие абсолютной сходимости и данную теорему, можно исследовать сходимость несобственных интегралов от знакопеременных функций, применяя признаки сравнения.

Пример. Исследуем на сходимость несобственный интеграл первого рода

от знакопеременной функции

.

Так как на промежутке

,

и интеграл сходится, то по признаку сравнения 1 исходный интеграл также сходится (абсолютно).

4 Обыкновенные дифференциальные уравнения

4.1 Общие понятия

Определение. Дифференциальным уравнением называется уравнение, содержащее производные или дифференциалы неизвестной функции.

Если неизвестная функция зависит только от одного аргумента, то дифференциальное уравнение называется обыкновенным.

Если же неизвестная функция зависит от двух или большего числа независимых переменных, то дифференциальное уравнение называется уравнением в частных производных.

Определение. Порядком n дифференциального уравнения называется порядок наивысшей производной или наивысшего дифференциала, входящих в уравнение.

В данном разделе будем изучать только обыкновенные дифференциальные уравнения, как правило, относительно неизвестной функции аргументаx.

Примеры

, , уравнение 1-го порядка;

,, уравнение 3-го порядка;

,, уравнение 6-го порядка.

Определение. Решением дифференциального уравнения называется функция , которая при подстановке в дифференциальное уравнение обращает его в верное равенство (тождество).

Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения, а действие интегрирования функций называется квадратурой.

При этом под квадратурой всегда будем понимать какую-либоодну первообразную.

Однако не всегда решение дифференциального уравнения может быть получено в виде явно заданной функции .

Пример

;

;

.

Обозначим

.

Определение. Уравнение ,которое определяет решение дифференциального уравнения как неявную функциюx, называется интегралом рассматриваемого дифференциального уравнения.