
- •Росжелдор
- •6.5 Вычисление тройного интеграла в декартовых координатах …………. 70
- •1 Неопределенный интеграл
- •1.1 Первообразная функция
- •1.2 Неопределенный интеграл
- •1.3 Основные свойства неопределенного интеграла
- •1.4 Таблица основных интегралов
- •1.5 Основные методы интегрирования
- •1.6 Интегрирование рациональных функций
- •1.7 Интегрирование выражений, содержащих тригонометрические функции
- •2.2 Основные свойства определенного интеграла
- •2.3 Производная определенного интеграла по переменному верхнему пределу
- •2.4 Формула Ньютона-Лейбница
- •2.5 Замена переменной в определенном интеграле
- •3.2 Несобственные интегралы второго рода (от неограниченных функций)
- •3.3 Признаки сходимости несобственных интегралов
- •3.4 Абсолютная и условная сходимости
- •4 Обыкновенные дифференциальные уравнения
- •4.1 Общие понятия
- •4.2 Дифференциальные уравнения первого порядка
- •4.3 Уравнение с разделяющимися переменными
- •4.5 Линейное уравнение
- •4.8 Уравнения высшего порядка, допускающие понижение порядка
- •1) Уравнение вида .
- •2) Уравнение вида .
- •3) Уравнение вида .
- •4.9 Линейные дифференциальные уравнения высшего порядка
- •4.10 Линейное однородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
- •1) Найти общее решение однородного дифференциального уравнения .
- •4.11 Линейное неоднородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
- •5 Системы обыкновенных дифференциальных уравнений
- •5.1 Нормальная система дифференциальных уравнений
- •5.2 Интегрирование нормальной системы методом исключения неизвестных
- •5.3 Нормальная система линейных дифференциальных уравнений с постоянными коэффициентами
- •5.4 Понятие устойчивости решения нормальной системы по Ляпунову
- •6 Кратные интегралы
- •6.1 Двойной интеграл
- •6.2 Вычисление двойного интеграла в декартовых координатах
- •6.3 Вычисление двойного интеграла в полярных координатах
- •6.4 Тройной интеграл
- •6.5 Вычисление тройного интеграла в декартовых координатах
- •6.6 Вычисление тройного интеграла в цилиндрических и сферических координатах
- •7 Криволинейные интегралы
- •7.1 Криволинейный интеграл первого рода
- •7.2 Криволинейный интеграл второго рода
- •7.3 Связь между криволинейными интегралами первого и второго рода
- •7.4 Формула Грина
- •8 Поверхностные интегралы
- •8.1 Поверхностный интеграл первого рода
- •8.2 Поверхностный интеграл второго рода
- •8.3 Связь между поверхностными интегралами первого и второго рода
- •8.4 Формула Остроградского
- •8.5 Формула Стокса
- •9 Практические задания
- •9.1 Неопределенные интегралы
- •9.2 Обыкновенные дифференциальные уравнения первого порядка
- •9.3 Обыкновенные дифференциальные уравнения высшего порядка
2.2 Основные свойства определенного интеграла
Свойство 1. Постоянный множитель можно выносить за знак интеграла:
 .
.
Доказательство:
 .
.
Свойство 2. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций:
 .
.
Доказательство:

 .
.
Свойство
3. Если
отрезок интегрирования
![]() разбить на два отрезка
разбить на два отрезка![]() и
и![]() ,
то интеграл по всему отрезку
,
то интеграл по всему отрезку![]() будет равен сумме интегралов по отрезкам
будет равен сумме интегралов по отрезкам![]() и
и![]() :
:
 .
.
Доказательство:

 .
.
Свойство 4. При перемене местами пределов интегрирования интеграл изменяет знак:
 .
.
Доказательство
следует из определения определенного
интеграла (![]() при
при![]() ).
).
Свойство 5. Интеграл с одинаковыми пределами интегрирования равен нулю:
 .
.
Доказательство
следует из свойства 4 (при
![]() ):
):
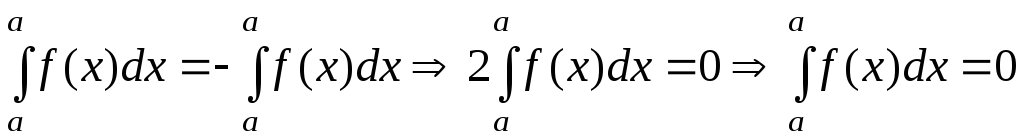 .
.
Свойство 6. Интеграл от постоянной величины равен этой постоянной, умноженной на длину отрезка интегрирования:
 .
.
Доказательство:
 .
.
Свойство 7. Если
m
и
M
– наименьшее и наибольшее значения
функции
![]() на отрезке
на отрезке![]() ,
то
,
то
 .
.
Доказательство
дается переходом к пределу при
![]() в очевидных неравенствах:
в очевидных неравенствах:
 .
.
Свойство 8. Абсолютная величина интеграла от данной функции не превышает интеграла от абсолютной величины этой же функции:
 .
.
Доказательство.
Так как на основании свойства абсолютной
величины числа
![]() для
для![]() ,
то
,
то

откуда при переходе
к пределу при
![]() получаем:
получаем:

а это равносильно неравенству, которое требовалось доказать.
Свойство
9 (Теорема
о среднем). Если
функция
![]() непрерывна на отрезке
непрерывна на отрезке![]() ,
то на этом отрезке существует такая
точкас,
что справедлива формула
,
то на этом отрезке существует такая
точкас,
что справедлива формула
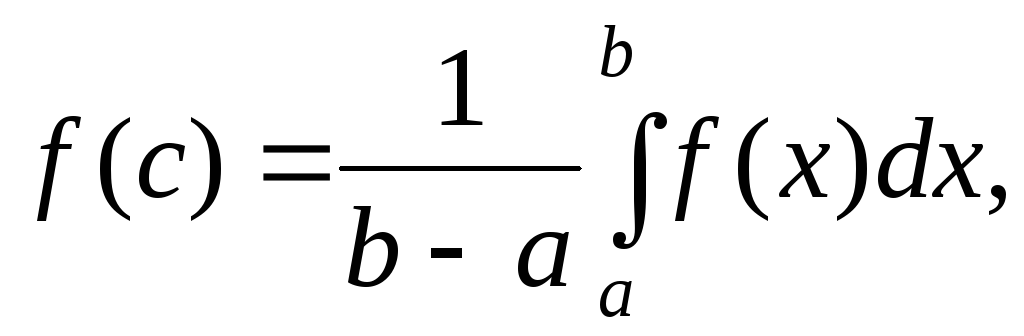
называемая формулой
среднего значения функции
![]() на отрезке
на отрезке![]() .
.
Доказательство.
Так как функция
![]() непрерывна на отрезке
непрерывна на отрезке![]() ,
то по второй теореме Вейерштрасса
,
то по второй теореме Вейерштрасса
![]() .
.
Отсюда на основании свойства 7 получаем
 или
или

Положим

Так как функция
![]() непрерывна на отрезке
непрерывна на отрезке![]() ,
то по второй теореме Больцано-Коши на
отрезке
,
то по второй теореме Больцано-Коши на
отрезке![]() найдется такая точкас,
что
найдется такая точкас,
что
![]() .
Поэтому
.
Поэтому

что и требовалось доказать.
2.3 Производная определенного интеграла по переменному верхнему пределу
Пусть
на отрезке
![]() задана непрерывная функция
задана непрерывная функция![]() .
.
Определение. Функция

называется определенным интегралом с переменным верхним пределом.
Теорема
2.2.
Производная определенного интеграла
от непрерывной на отрезке
![]() функции по переменному верхнему пределу
равна значению подынтегральной функции
на верхнем пределе:
функции по переменному верхнему пределу
равна значению подынтегральной функции
на верхнем пределе:
 .
.
Доказательство.
Дадим аргументу
![]() приращение
приращение![]() .
Найдем приращение функции
.
Найдем приращение функции![]() ,
используя свойство 3 определенного
интеграла:
,
используя свойство 3 определенного
интеграла:
 .
.
Применяя к последнему интегралу теорему о среднем (свойство 9), получим
 ,
,
где с
заключено
между
![]() и
и![]() .
.
Согласно определению производной имеем
![]() .
.
Так как
![]() ,
то
,
то![]() ,
и в силу непрерывности подынтегральной
функциина
отрезке
,
и в силу непрерывности подынтегральной
функциина
отрезке
![]()
![]() .
.
Следовательно,
![]() .
.
Таким образом,
доказана теорема 1.2 существования
первообразной для непрерывной на отрезке
![]() функции
функции![]() ,
причем первообразной для
,
причем первообразной для![]() является определенный интеграл с
переменным верхним пределом
является определенный интеграл с
переменным верхним пределом![]() :
:
 .
.
2.4 Формула Ньютона-Лейбница
С помощью теоремы 2.2 выведем основную формулу интегрального исчисления – формулу Ньютона-Лейбница. Эта формула дает способ вычисления определенного интеграла через первообразную от подынтегральной функции, не прибегая к составлению интегральной суммы и к вычислению ее предела.
Теорема
2.3. Если
![]() есть какая-либо первообразная от
непрерывной на отрезке
есть какая-либо первообразная от
непрерывной на отрезке
![]() функции
функции![]() ,
то справедливаформула
Ньютона-Лейбница:
,
то справедливаформула
Ньютона-Лейбница:
 .
.
Доказательство.
По теореме 2.2 функция
![]() является первообразной от функции
является первообразной от функции![]() на отрезке
на отрезке![]() ,
т.е.
,
т.е.
 .
.
Определим постоянную
С,
подставляя в это равенство значение
![]() и используя свойство 5 определенного
интеграла:
и используя свойство 5 определенного
интеграла:
![]() ,
так как
,
так как
![]() .
.
Тогда
 .
.
Полагая в полученном
равенстве
![]() и затем заменяя переменную интегрированияt
на x,
получаем формулу Ньютона-Лейбница.
и затем заменяя переменную интегрированияt
на x,
получаем формулу Ньютона-Лейбница.
Пример
 .
.
