2.5 Замена переменной в определенном интеграле

Теорема 2.4. Пусть – непрерывная функцияна отрезке . Тогда, если: 1) функциядифференцируема на отрезкеинепрерывна на ; 2) множеством значений функцииявляется отрезок; 3)и, то справедливаформула замены переменной в определенном интеграле:

.

Доказательство. По формуле Ньютона-Лейбница

,

где – первообразная для функции на отрезке . Рассмотрим на отрезкесложную функцию. Применяя правило дифференцирования сложной функции, находим

.

Отсюда следует, что функция является первообразной для функциии непрерывной на отрезке, а поэтому согласно формуле Ньютона-Лейбница получаем

.

Пример

.

2.6 Интегрирование по частям в определенном интеграле

Теорема 2.5. Если функции иимеют непрерывные производные на отрезке , то справедливаформула интегрирования по частям в определенном интеграле:

.

Доказательство. Так как функция является первообразной для функции, то по формуле Ньютона-Лейбница

.

Отсюда, используя свойство 2 определенного интеграла, получаем

,

или, так как и

,

откуда и следует доказываемая формула.

Пример

3 НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

3.1 Несобственные интегралы первого рода

(с бесконечными пределами)

Обобщим понятие определенного интеграла на случай бесконечного промежутка интегрирования.

Определение. Несобственным интегралом первого рода от функции , непрерывной на промежутке, называется предел определенного интегралас переменным верхним пределомR при :

.

Если указанный предел существует, то несобственный интеграл называется сходящимся, а если предел не существует, то расходящимся.

Из определения и рис. 3.1 следует геометрический смысл несобственного интеграла первого рода: несобственный интеграл первого рода от неотрицательной функции численно равен площади криволинейной трапеции с бесконечно длинным основанием.

Рис. 3.1. Геометрический смысл несобственного интеграла первого рода

Аналогично вводится несобственный интеграл первого рода по промежутку :

.

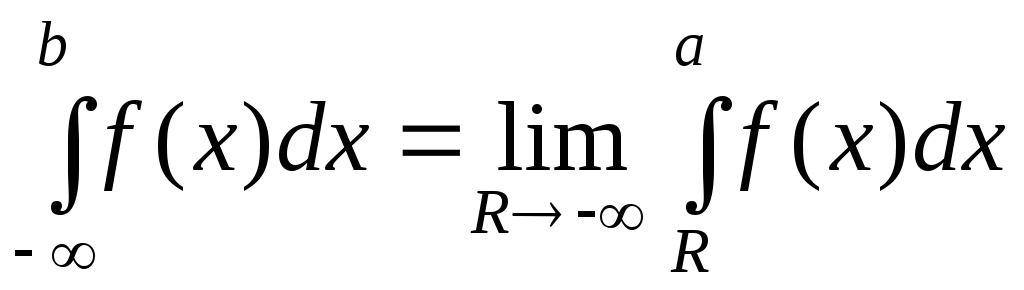Можно определить и несобственный интеграл первого рода с двумя бесконечными пределами, т.е. по промежутку :

,

где с – любое число.

Пример 1

т.е. данный интеграл сходится.

Пример 2

т.е. данный интеграл расходится, так как предел функции прине существует.

3.2 Несобственные интегралы второго рода (от неограниченных функций)

Обобщим понятие определенного интеграла на случай подынтегральной функции, неограниченной на промежутке интегрирования.

Определение. Несобственным интегралом второго рода от функции , непрерывной на промежуткеи имеющей бесконечный разрыв при, называется предел определенного интеграла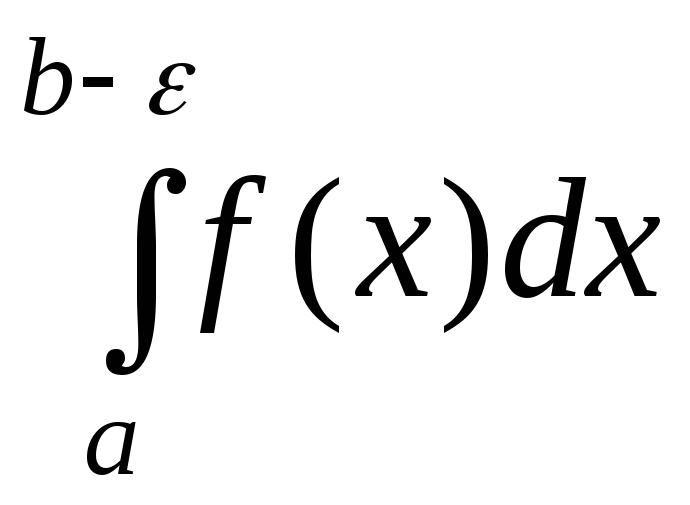с переменным верхним пределомпри:

.

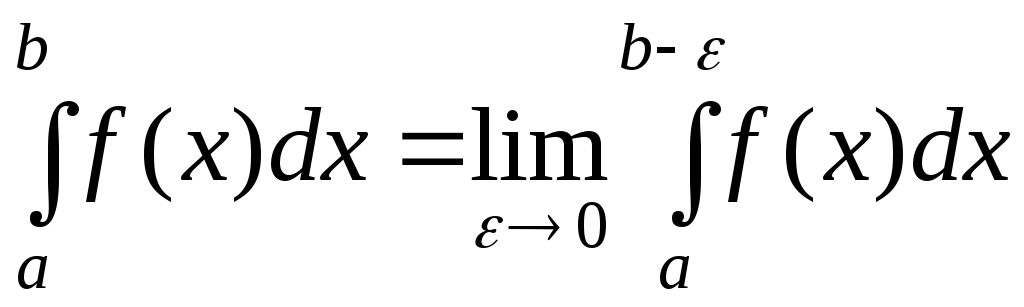Если указанный предел существует, то несобственный интеграл называется сходящимся, а если предел не существует, то расходящимся.

Из определения и рис. 3.2 следует геометрический смысл несобственного интеграла второго рода: несобственный интеграл второго рода от неотрицательной функции численно равен площади криволинейной трапеции с бесконечно длинной высотой.

Рис. 3.2. Геометрический смысл несобственного интеграла второго рода

Аналогично вводится несобственный интеграл второго рода от функции , непрерывной на промежуткеи имеющей бесконечный разрыв при:

.

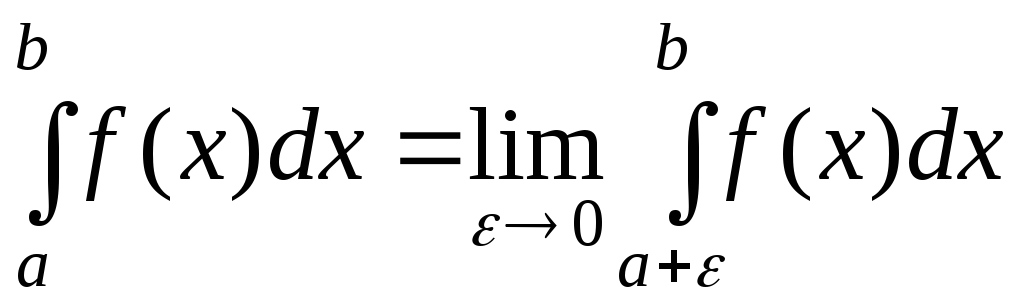Можно определить и несобственный интеграл второго рода от функции , имеющей бесконечный разрыв в некоторой внутренней точкес промежутка :

.

Пример

,

т.е. данный интеграл сходится.