
- •Росжелдор
- •6.5 Вычисление тройного интеграла в декартовых координатах …………. 70
- •1 Неопределенный интеграл
- •1.1 Первообразная функция
- •1.2 Неопределенный интеграл
- •1.3 Основные свойства неопределенного интеграла
- •1.4 Таблица основных интегралов
- •1.5 Основные методы интегрирования
- •1.6 Интегрирование рациональных функций
- •1.7 Интегрирование выражений, содержащих тригонометрические функции
- •2.2 Основные свойства определенного интеграла
- •2.3 Производная определенного интеграла по переменному верхнему пределу
- •2.4 Формула Ньютона-Лейбница
- •2.5 Замена переменной в определенном интеграле
- •3.2 Несобственные интегралы второго рода (от неограниченных функций)
- •3.3 Признаки сходимости несобственных интегралов
- •3.4 Абсолютная и условная сходимости
- •4 Обыкновенные дифференциальные уравнения
- •4.1 Общие понятия
- •4.2 Дифференциальные уравнения первого порядка
- •4.3 Уравнение с разделяющимися переменными
- •4.5 Линейное уравнение
- •4.8 Уравнения высшего порядка, допускающие понижение порядка
- •1) Уравнение вида .
- •2) Уравнение вида .
- •3) Уравнение вида .
- •4.9 Линейные дифференциальные уравнения высшего порядка
- •4.10 Линейное однородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
- •1) Найти общее решение однородного дифференциального уравнения .
- •4.11 Линейное неоднородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
- •5 Системы обыкновенных дифференциальных уравнений
- •5.1 Нормальная система дифференциальных уравнений
- •5.2 Интегрирование нормальной системы методом исключения неизвестных
- •5.3 Нормальная система линейных дифференциальных уравнений с постоянными коэффициентами
- •5.4 Понятие устойчивости решения нормальной системы по Ляпунову
- •6 Кратные интегралы
- •6.1 Двойной интеграл
- •6.2 Вычисление двойного интеграла в декартовых координатах
- •6.3 Вычисление двойного интеграла в полярных координатах
- •6.4 Тройной интеграл
- •6.5 Вычисление тройного интеграла в декартовых координатах
- •6.6 Вычисление тройного интеграла в цилиндрических и сферических координатах
- •7 Криволинейные интегралы
- •7.1 Криволинейный интеграл первого рода
- •7.2 Криволинейный интеграл второго рода
- •7.3 Связь между криволинейными интегралами первого и второго рода
- •7.4 Формула Грина
- •8 Поверхностные интегралы
- •8.1 Поверхностный интеграл первого рода
- •8.2 Поверхностный интеграл второго рода
- •8.3 Связь между поверхностными интегралами первого и второго рода
- •8.4 Формула Остроградского
- •8.5 Формула Стокса
- •9 Практические задания
- •9.1 Неопределенные интегралы
- •9.2 Обыкновенные дифференциальные уравнения первого порядка
- •9.3 Обыкновенные дифференциальные уравнения высшего порядка
6.3 Вычисление двойного интеграла в полярных координатах
В двойном интеграле, как и в определенном, замена переменных – важнейший метод приведения интеграла к виду, более удобному для вычисления.
Наиболее важным
для практических приложений частным
случаем замены переменных является
замена декартовых координат x
и y
полярными координатами – радиусом-вектором
r
и полярным углом
![]() (переход из декартовой системы координат
в полярную)
(переход из декартовой системы координат
в полярную)
![]()
по формуле
![]() .
.
Выражение
![]() называют обычно элементом площади в
полярных координатах.
называют обычно элементом площади в
полярных координатах.
Вычисление двойного
интеграла в полярных координатах, так
же как и в полярных, сводится к вычислению
повторного интеграла, но только роль
переменных
![]() играют теперь
играют теперь![]() .
.
Пример. Вычислить двойной интеграл
![]() ,
,
где G
– четверть
круга
![]() ,
расположенная в первом квадранте.
,
расположенная в первом квадранте.
Очевидно,
что в области G
радиус-вектор r
изменяется в пределах от 0 до 1, а угол
![]() – от 0 до
– от 0 до![]() (рис. 6.5).
(рис. 6.5).
Тогда получаем


Рис. 6.5. Пример вычисления двойного интеграла в полярных координатах
6.4 Тройной интеграл
Пусть
функция
![]() определена и непрерывна в замкнутой
ограниченной области
определена и непрерывна в замкнутой
ограниченной области![]() трехмерного пространства
трехмерного пространства![]() .
.
Разобьем
область
![]() произвольным образом наn
частей
произвольным образом наn
частей
![]() с
объемами
с
объемами![]()
![]() .
В каждой частичной области
.
В каждой частичной области![]() выберем произвольную точку
выберем произвольную точку![]() и составим сумму
и составим сумму
 ,
,
которую
назовем интегральной
суммой для
функции
![]() в области
в области![]() .
.
Назовем диаметром области d наибольшее расстояние между граничными точками этой области. Например, диаметром области, представляющей собой эллипсоид, будет его удвоенная наибольшая полуось.
Обозначим
через
![]() наибольший из диаметров частичных
областей
наибольший из диаметров частичных
областей![]() :
:
![]() .
.
Определение.
Тройным
интегралом от
функции
![]() по области
по области![]() называется предел интегральных сумм
при
называется предел интегральных сумм
при![]() ,
если этот предел существует и не зависит
ни от способа разбиения области
,
если этот предел существует и не зависит
ни от способа разбиения области
![]() на частичные
области
на частичные
области
![]() ,
ни от выбора в каждой из них точки
,
ни от выбора в каждой из них точки
![]() :
:

или в другой записи:
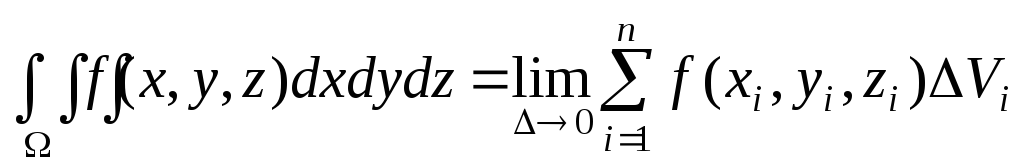 .
.
Функция
![]() называетсяинтегрируемой
в области
называетсяинтегрируемой
в области
![]() ,
область
,
область
![]() – областью
интегрирования,
x,
y,
z
– переменными
интегрирования,
– областью
интегрирования,
x,
y,
z
– переменными
интегрирования,
![]() –
элементом
объема.
–
элементом
объема.
Теорема
6.2 (существования тройного интеграла)
(без доказательства).
Функция
![]() ,
непрерывная в замкнутой ограниченной
области
,
непрерывная в замкнутой ограниченной
области![]() ,
интегрируема в этой области.
,
интегрируема в этой области.
Замечание.
Если положить
![]() всюду в области
всюду в области
![]() ,
то из определения тройного интеграла
легко получить формулу для вычисления
объема V
области
,
то из определения тройного интеграла
легко получить формулу для вычисления
объема V
области
![]() с помощью тройного интеграла
с помощью тройного интеграла

или
![]() .
.
Основные свойства тройного интеграла аналогичны соответствующим свойствам двойного интеграла.
Свойство 1. Постоянный множитель можно выносить за знак интеграла:
![]() .
.
Свойство 2. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций:
![]() .
.
Свойство
3. Если
область интегрирования
![]() разбить на две непересекающиеся области
разбить на две непересекающиеся области
![]() и
и
![]() ,
то интеграл по всей области
,
то интеграл по всей области
![]() будет равен сумме интегралов по областям
будет равен сумме интегралов по областям
![]() и
и
![]() :
:
![]() .
.
Свойство 4
(Теорема о среднем).
Если функция
![]() непрерывна в замкнутой ограниченной
области
непрерывна в замкнутой ограниченной
области
![]() ,
то в этой области существует такая точка
,
то в этой области существует такая точка
![]() ,
что справедлива формула
,
что справедлива формула
 ,
,
где V
– объем области
![]() .
.
6.5 Вычисление тройного интеграла в декартовых координатах
Вычисление тройного интеграла сводится к последовательному вычислению одного однократного (определенного) и одного двойного интегралов или к вычислению, в конечном итоге, трех однократных (определенных) интегралов следующим способом.
Пусть область
![]() (рис. 6.6) ограничена снизу поверхностью
(рис. 6.6) ограничена снизу поверхностью
![]() ,
сверху поверхностью
,
сверху поверхностью![]() ,
а с боковых сторон цилиндрической
поверхностью, и пустьG
– проекция
области
,
а с боковых сторон цилиндрической
поверхностью, и пустьG
– проекция
области
![]() на плоскость
на плоскость![]() ,
причем всюду в областиG
функции
,
причем всюду в областиG
функции
![]() и
и![]() непрерывны и
непрерывны и![]() .
.

Рис.6.6. Вычисление тройного интеграла в декартовых координатах
Тогда тройной интеграл вычисляется по формуле
 ,
,
причем сначала вычисляется внутренний определенный интеграл по переменной z (при постоянных x и y), а затем внешний двойной интеграл по области G.
Записывая двойной интеграл через один из повторных (см. п. 6.2), получаем
 .
.
Замечание.
Аналогичные
формулы для вычисления тройного интеграла
можно записать и для случаев проектирования
области
![]() на плоскости
на плоскости![]() и
и![]() .
.
Пример. Вычислить тройной интеграл
![]() ,
,
где область
интегрирования
![]() – пирамида,
ограниченная плоскостью
– пирамида,
ограниченная плоскостью
![]() и координатными плоскостями
и координатными плоскостями![]() (рис. 6.7).
(рис. 6.7).

Рис. 6.7. Пример вычисления тройного интеграла в декартовых координатах
Область
![]() проектируется на плоскость
проектируется на плоскость![]() в треугольникG,
ограниченный прямыми
в треугольникG,
ограниченный прямыми
![]() .
Полагая
.
Полагая
![]()
и используя сначала формулу для вычисления тройного интеграла, а затем первую формулу для вычисления двойного интеграла, получим:

![]()

