1 Неопределенный интеграл

1.1 Первообразная функция

В дифференциальном исчислении по заданной функции приходилось отыскивать ее производную.

В интегральном исчислении рассматривается обратная задача: по заданной функции восстановить такую функцию, для которойбыла бы производной, т.е..

Определение. Функция называетсяпервообразной (функцией) для функции на интервале, если для всех значенийx из этого интервала выполняется равенство

.

Примеры

1) Функция является первообразной для функциина всей числовой прямой, так как при любом значениивыполняется равенство.

2) Функция является первообразной для функциина интервале, так как в любой точкеx этого интервала .

Однако задача отыскания по данной функции её первообразной решается неоднозначно. Действительно, если– первообразная для, т.е., то функция, где– произвольная постоянная, также является первообразной для, так какдля любого числа.

Например, для первообразной является не только, но и функция, так как.

Возникает вопрос: если и– две первообразные для одной и той же функции, то всегда ли они отличаются друг от друга на постоянное слагаемое? Оказывается, что это действительно так.

Теорема 1.1. Если и– две первообразные для функциина интервале, то, где– некоторая постоянная.

Доказательство. По условию и– первообразные для, поэтому

.

Рассмотрим функцию

.

Её производная

.

Для любых двух точек по теореме Лагранжа получаем

.

Так как , то. Это означает, что значения функцииво всех точках интервалаодинаковы, т.е., где– некоторое число. Таким образом,или.

Следствие. Все первообразные для функции на интерваледаются формулой, где– одна из первообразных для, а– произвольная постоянная.

1.2 Неопределенный интеграл

Определение. Совокупность всех первообразных для функции на интерваленазываетсянеопределенным интегралом от функции на этом интервале и обозначается символом

.

При этом функция называетсяподынтегральной функцией, –подынтегральным выражением, а переменная x – переменной интегрирования.

Нахождение первообразных для функции называетсяинтегрированием функции .

Отметим, что подынтегральное выражение является дифференциалом первообразной:

.

Примеры

1) , так как.

2) , так как.

Теорема 1.2. Если функция непрерывна на интервале, то для неё существует первообразная на, а следовательно, и неопределенный интеграл.

Доказательство этой теоремы будет дано позже (см. теорему 2.2).

1.3 Основные свойства неопределенного интеграла

Свойство 1. Производная от неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению:

_{и .}

Доказательство.

;

.

Свойство 2. Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная:

.

Доказательство.

.

Свойство 3. Постоянный множитель можно выносить за знак интеграла:

.

Доказательство. Прежде всего подчеркнем, что данное равенство имеет условный характер: его следует понимать как равенство правой и левой частей с точностью до произвольного постоянного слагаемого, поскольку каждый из интегралов определен с точностью до произвольного постоянного слагаемого.

Действительно, пусть – первообразная для функции, т.е.. Тогда– первообразная для функции, так как. Отсюда следует, что

,

где – произвольная постоянная.

Свойство 4. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от этих функций:

.

Доказательство. Данное равенство (как и в предыдущем свойстве) следует понимать как равенство правой и левой частей с точностью до произвольного постоянного слагаемого, поскольку каждый из интегралов определен с точностью до произвольного постоянного слагаемого.

Действительно, пусть и– первообразные для функцийисоответственно, т.е.. Тогда функцияявляется первообразной для функции, так как

.

Следовательно,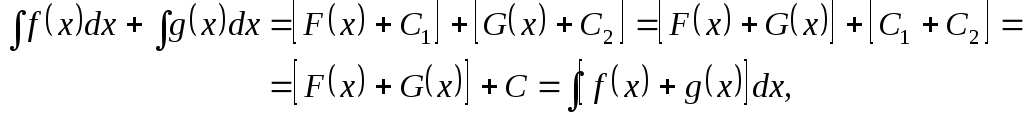

где – произвольная постоянная.

Отметим, что данное свойство справедливо для любого конечного числа слагаемых функций.