3 Тема: Элементы векторной алгебры.

а) операции над векторами

Обобщим понятия о векторах , известные со школьного курса геометрии

Вектором называется направленный отрезок АВ

Обозначается двумя заглавными или одной строчной буквой.

Длина(модуль) вектора АВ обозначается .

Два вектора расположенные на одной прямой или на двух паралельных прямых называются коллиниарными.

Три вектора расположенные в одной плоскости.

Суммой векторов и называется вектор =+, здесь вектор соединяет начало вектора с концом вектора (правило треугольника).

Кроме того, сумма векторов и определяется как диагональ параллелограма, построенного на этих векторах (правило параллелограмма).

Произведением вектора на число k называется вектор =k*, удовлетворяющий условиям: 1.Длина =* 2. направление вектора совпадает с направлением вектора в, если k>0 и протиположно направленный если k<0 .

Аналогично можно определить сумму нескольких векторов, например сумма четырех векторов будет вектор начало которого совпадет сначалом вектора , а конец с концом вектора ( правило многоугольника).

Сумма векторов и,не лежащих в одной или паралельных плоскостях, есть вектор определяемый диагональю параллепипеда построенного ан векторах (правило параллелпипеда).

Разность векторов и есть вектор равный сумме вектора и вектора противоположного вектору т.е. ( - ).

Если на векторах и построен параллелограмм, то одна диагональ есть сумма, а вторая есть их разность.

Если на множестве определены две операции, которые удовлетворяют законам сложения и умножения на число, тотакое множество называется векторным пространством.

Система векторов называется базисом векторного пространства, если она удовлетворяет условиям:

1. система векторов линейно независима

2. любой вектор векторного пространства линейно выражается через эти вектора

Число векторов базиса называется размерностью пространства.

Разложение вектора по базисным векторам имеет вид: , здесь коэффициенты перед базисными векторами называются координатами вектора. В двумерном пространстве вектор имеет координаты-={х,y}, а в трехмерном пространстве = {х,у,z}.

Тогда для векторов и координаты суммы и разности будут определятся соответственно (1)

А координаты произведения вектора на число λ будут .

б) Скалярное произведение векторов.

Определение: Скалярным произведением () векторов и называется число равное произведению длин векторов на косинус угла между ними

() = (2)

Определим скалярное произведение векторов и через координаты этих векторов. Для векторов , , скалярное произведение равно: (3).

Скалярное произведение двух векторов равно сумме произведений соответствующих координат. Если болса, то , =1 и , тогда длина вектора будет (4).

Угол между векторами и определяется по формуле

(5).

Таким образом, скалярное произведение применяется при нахождении длин и величин углов.

в) Векторное произведение векторов и его свойства

В векторном пространстве V рассмотрим ортонормированный базис R= . Пусть неколлениарные векторы.

Определение. Векторным произведением векторов и называется вектор, обозначаемый и удовлетворяющий следующим условиям:

1)

2)

3)Тройки векторов одинаково ориентированы.

Если векторы и коллинеарны, то их векторное произведение равно нулю. Пусть векторы заданы своими координатами и неколлинеарны:

Тогда ранг 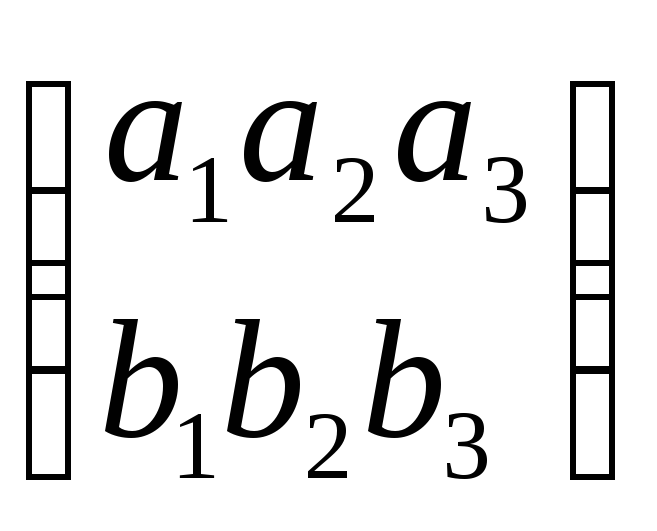=2, отсюда векторное произведение не равно нулю. Координаты этого вектора относительно базиса удовлетворяют системе уравнений , определитель которой отличен от нуля:

(3)

(2),(3) .

Из первого условия определения найдем необходимое значение для t. Изветно, что

sin

(4) тогда .

Здесь

После вычислений находим:

(5)

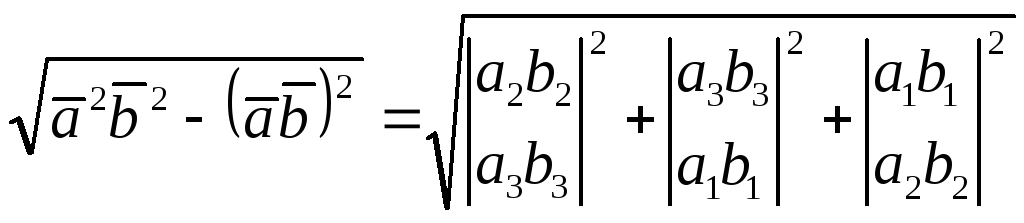
(6)

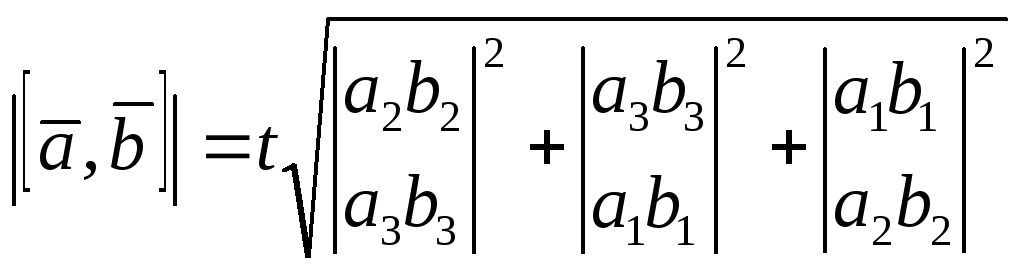
(4),(5),(6) (7)

(1), (2), (7)

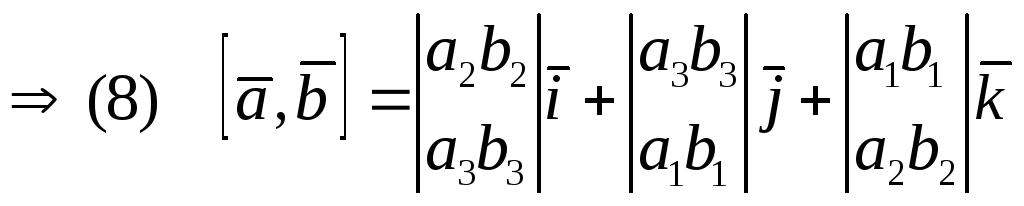
Если векторы коллинеарны, то ранг 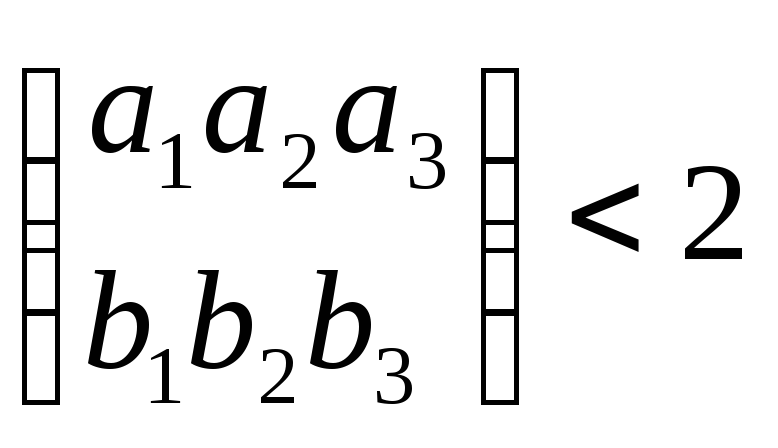и (8) формуле каждый определитель равен нулю. По определению ПОэтому и в этом случае (8) формула справедлива. Таким образом, доказана теорема.

ТЕОРЕМА. Если

то

(8) формулу удобно записывать следующим образом:

(9)

Свойства векторного произведения.

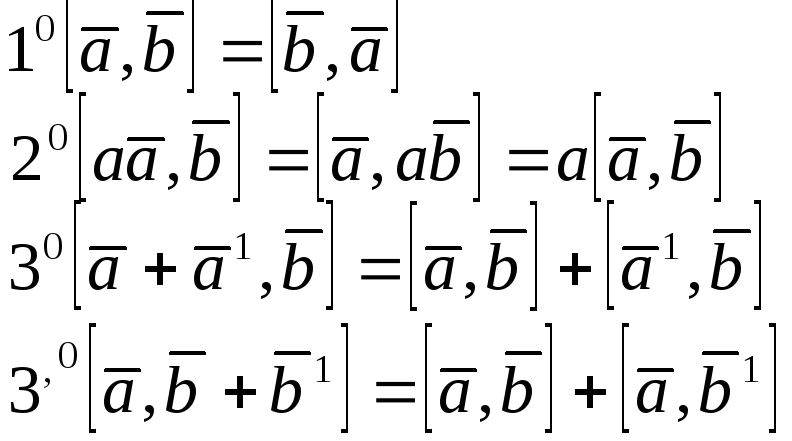
1), 2), 3) свойства следуют из (8) формулы.

Применение векторного произведения.

1. Модуль векторного произведения равен площади параллелограммаABCD

2. Площадь треугольника равна :

Смешанное произведение векторов и его свойства .

Пусть положительно ориентированный ортонормированный базис.

Определение Смешанным произведением векторов называется число обозначаемое и равное скалярному произведению вектора на векторное произведение векторов и .

Таким образом, - число.

1-ТЕОРЕМА (геометрический смысл смешанного проиведения).Если - три некомпланарных вектора и , то абсолютное значение смешанного произведения равно объему параллелипипеда построенного на векторах :

(1)

2- ТЕОРЕМА. Если в базисе координаты векторов , то

(2)

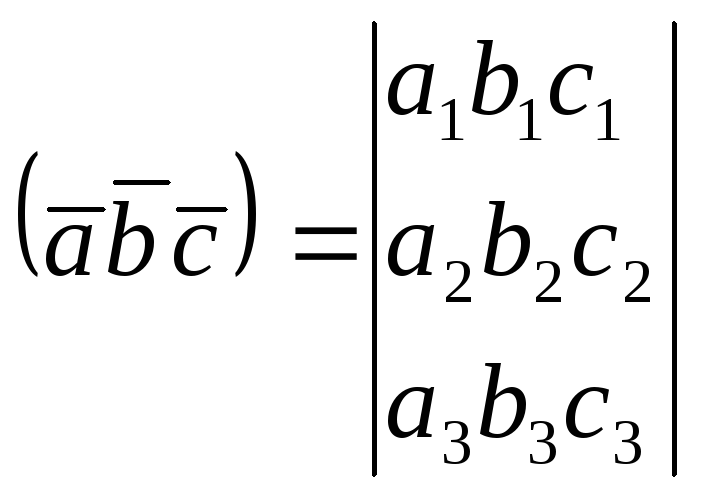
Свойства смешанного произведения:

Применение смешанного произведения.

Пусть относительно прямоугольной системы координат тетраэдр ABCD задан своими вершинами:

. Тогда его объем находится по формуле:

.
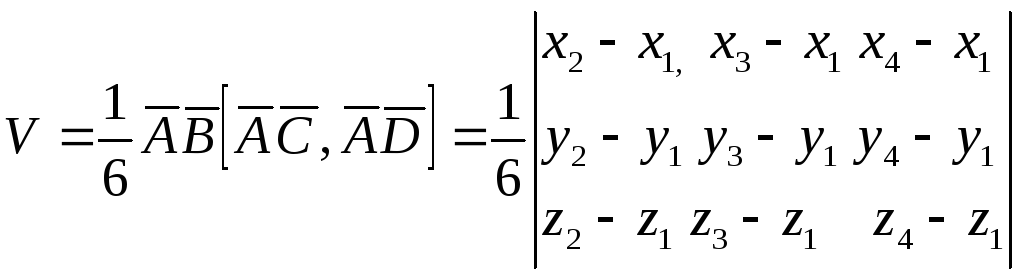