
- •Учреждение «Университет «Туран»
- •Содержание
- •5В071900 - Радиотехника, электроника и телекоммуникации
- •Математика 1 Пояснительная записка
- •2 Примерный перечень практических занятий
- •Учреждение «Университет «Туран»
- •Рабочая программа по дисциплине: «Математика 1»
- •Пояснительная записка
- •Общие данные по рабочей программе.
- •Общее описание рабочей программы
- •Иметь представление о роли аналитической геометрии и линейной алгебры в прикладных исследованиях;
- •Основная часть тематика лекционных занятий
- •Тематика практических занятий
- •Тематика самостоятельной работы
- •Тематика срсп
- •Список рекомендуемой литературы
- •Учреждение «Университет «Туран»
- •Силлабус по дисциплине: «Математика 1»
- •Описание изучаемой дисциплины (пояснительная записка)
- •Общие данные по рабочей программе.
- •Общее описание рабочей программы
- •Иметь представление о роли аналитической геометрии и линейной алгебры в прикладных исследованиях;
- •Темы и продолжительность их изучения
- •Тематика практических занятий
- •Задания самостоятельной работы
- •Рубежный контроль
- •Критерии оценки знаний обучающихся (обобщенные)
- •Определение итоговой оценки по вск
- •Итоговая оценка
- •Вопросы для проведения контроля
- •Требования преподавателя
- •Правила поведения на аудиторных занятиях
- •Методические указания
- •График выполнения и сдачи заданий по дисциплине
- •Учреждение «Университет «Туран»
- •1 Тема: Матрицы и определители
- •2 Тема: Система линейных уравнений.
- •3 Тема: Элементы векторной алгебры.
- •4 Тема: Аналитическая геометрия на плоскости
- •1. Различные уравнения прямой
- •1.2 Уравнение прямой, проходящей через две точки
- •1.3 Нормальное уравнение прямой
- •5 Тема: кривые второго порядка
- •6 Тема: Аналитическая геометрия в пространстве
- •7 Тема: Поверхности второго порядка
- •Глоссарий
- •Глоссарий
- •12 Тема. Дифференцирование неявных и параметрически заданных функций
- •13 Тема. Дифференциал функции
- •Глоссарий
- •План практических занятий
- •Методические рекомендации по изучению дисциплины
- •«Математика 1»
- •(По работе с учебно-методическим комплексом)
- •Основания, целевая аудитория и ориентированность учебно-методического комплекса
- •Структура, содержание и образовательные возможности учебно-методического комплекса
- •Рекомендуемый порядок работы с учебно-методическим комплексом
- •Материалы для самостоятельной работы обучающегося по дисциплине «Математика 1»
- •Тема 1. Матрицы и определители. Системы линейных алгебраических уравнений.
- •Материалы по контролю и оценке учебных достижений обучающихся
- •Карта обеспеченности дисциплины учебной и учебно-методической литературой
Глоссарий
|
№ п/п |
Новые понятия |
Содержание |
|
1 |
Производная
функции в точке
|
Предел
отношения приращения функции
|
|
2. |
Основные правила дифференцирования |
|
|
3. |
Производные основных элементарных функций |
6.
|
|
4. |
Производная сложной функции |
Если
|
|
5. |
Производная обратной функции |
Если
|
|
6. |
Производная функции, заданной параметрическими уравнениями |
Если
|
|
7. |
Дифференциал функции |
|
|
8. |
Экономический смысл производной |
Производная
|
|
9. |
Формула Лагранжа |
|
|
10. |
Правило Лопиталя |
|
12 Тема. Дифференцирование неявных и параметрически заданных функций
Неявно заданная функция
Если функция задана уравнением у =f (х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявнъм заданием функции понимают задание функции в виде
уравнения F(х; у) = 0, не разрешенного относительно у.
Всякую явно заданную функцию у=f(х) можно записать как неявно
заданную уравнением f(х) - у = 0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относи-
тельно
у (например, у + 2х + соsy- 1 = 0 или ![]() — х + у = 0).
— х + у = 0).
Если неявная функция задана уравнением F(х; у) = 0, то для нахо-
ждения производной от-у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение
по х, рассматривая прп этом у как функцию х, и полученное затем
уравнение разрешить относительно у’.
Производная неявной функции выражается через аргумент х и функ-
цию .
Пример 21.1. Найти производную функции у, заданную уравнением
x3 + у3 — 3ху=0.
Решение: Функция у задана неявно. Дифференцируем по х равенство
х3 + у3 — 3ху=0.
Из полученного соотношения
3х2+3у2у’—3(1![]() у+х
у+х![]() у
у![]() )=0
)=0
следует,
что у2у![]() — ху
— ху![]() = у — х
= у — х![]() ,
т. е. у
,
т. е. у![]() =
=![]()
Функция, заданная параметрически
Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений
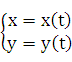
(21.1)
где — вспомогательная переменная, называемая параметром.
Найдем
производную ![]() ,
считая, что функции (21.1) имеют производ-
,
считая, что функции (21.1) имеют производ-
ные и что функция х = х( t). По правилу дифференцирования обратной функции
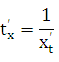
(21.2)
Функцию у = f(х), определяемую параметрическими уравнениями
(21.1),
можно рассматривать как сложную функцию
у = у(t), где t=![]()
По
правилу дифференцярования сложной
функции имеем;![]()
С учетом равенства (21.2) получаем
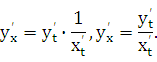

Полученная
формула позволяет находить производную![]() от
функции
от
функции
заданной параметрически, не находя непосредственной зависимости у от х.
Пример
21.2.
Пусть 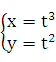 Найти
Найти ![]() .
.
Решение:
Имеем ![]() .
Следовательно,
.
Следовательно, ![]() т.
е.
т.
е.
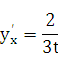
В этом можно убедиться, найдя непосредственно зависимость у от х.
Действительно,
t=![]() Тогда у=
Тогда у=![]() Отсюда
Отсюда ![]() т. е. у=.
т. е. у=.![]()
ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать. А затем результат продиффернцировать. Такую операцию называют логарифмическим дифференцированием.
Пример
22.1. Найти
производную функции y=![]()
Решение:
Можно
найти ![]() с помощью правил и формул дифференци-
рования. Однако такой способ слишком
громоздкий. Применим логарифмическое
дифференцирование. Логарифмируем
функцию:
с помощью правил и формул дифференци-
рования. Однако такой способ слишком
громоздкий. Применим логарифмическое
дифференцирование. Логарифмируем
функцию:
![]() .
.
Дифференцируем это равенство по х:
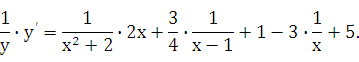
Выражаем
![]() :
:

т.
е.![]()
Существуют
функции, производные которых находят
лишь логарифмическим дифференцированием.
К их числу относится так называемая
степенно-показатаельная
функция y=![]() ,
где u= u(х) и
,
где u= u(х) и ![]() (х)
(х)
— заданные дифференцируемые функции от х. Найдем производную этой функции:
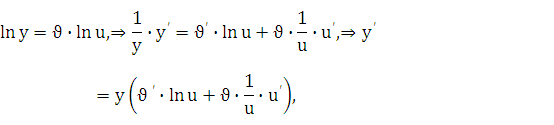
т. е.
![]()
или .

![]()
Сформулируем правило запоминания формулы (22.1):производная
степенно-показательной
функции равна сумме производной
показательной функции, при условии u=
соnst, и производной степенной при условии
![]() =
=
Пример
22.2.
Найти производную функции у =![]() .
.
Решение: Пользуясь формулой (22.1), получаем:
![]() .
.
Отметим, что запоминать формулу (22.1) необязательно, легче запомнить суть логарифмического дифференцирования.
ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
Производные высших порядков явно заданной функции
Производная
![]() (х)
функции у = f(х) есть также функция от х
и называется производной
первого порядка.
(х)
функции у = f(х) есть также функция от х
и называется производной
первого порядка.
Если
функция ‚![]() (х)
дифференцируема, то ее производная
называется
(х)
дифференцируема, то ее производная
называется
производной
второго порядка и
обозначается ![]() (или
(или![]() х),
х),![]()
Итак
![]() .
.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у” (или ‚“(х),
Итак,
![]() ,
,![]()
Производной n-го порядка (или n-й производной) называется производная от производной (n— 1) порядка:
![]()
Производные порядка выше первого называются производными высших порядков.
Начиная
с производной четвертого порядка,
производные обозначают римскими цифрами
или числами в скобках (![]() или
или ![]() — производная пятого порядка).
— производная пятого порядка).
.
Механический смысл производной второго порядка
Пусть материальная точка М движется прямолинейно по закону
S=
f(t). Как уже известно, производная ![]() равна
скорости точки в дан-
равна
скорости точки в дан-
ный
момент времени: ![]() .
.
Покажем, что вторая пронзводная от пути по времекп есть величина
ускореня
прямолинейного движения точки,
т. е. ![]() =
а.
=
а.
Пусть
в момент времени t скорость точки равна
V, а в момент t+![]() -
-
скорость
равна V+ ![]() ,
т. е. за промежуток времени
,
т. е. за промежуток времени ![]() .
скорость измени-
.
скорость измени-
лась
на величину ![]() .
.
Отношение
![]() выражает среднее ускорение движения
точки за время
выражает среднее ускорение движения
точки за время ![]() .
Предел этого отношения при
.
Предел этого отношения при ![]() называется ускорением точки М
называется ускорением точки М
в
данный момент t и обозначается буквой
а:![]()
![]() .
.
Но
V=![]() .
Поэтому а= (
.
Поэтому а= (![]() )
)![]() ,
т. е. а =
,
т. е. а =![]() ‘
‘
.Производные высших порядков от функций, заданных параметрически
Пусть функция у = f(х) задана параметрическими уравнениями
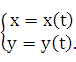
Как
известно, первая производная ![]() у
находится по формуле
у
находится по формуле
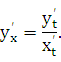
(23.1)
Найдем вторую производную от функции заданной параметрически.
Из определения второй производной и равенства (23.1) следует, что
![]() ,
т.е.
,
т.е.
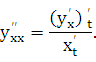

Аналогично получаем
![]() ,…
,…
Пример
23.3.
Найти вторую производную функции ![]()
Решение: По формуле (23.1)
![]() .
.
Тогда по формуле (23.2)
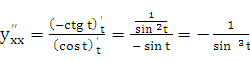 .
.
Заметим,
что найти ![]() можно по преобразованной формуле (23.2):
можно по преобразованной формуле (23.2):

запоминать которую вряд ли стоит.
