- •Учреждение «Университет «Туран»
- •Содержание
- •5В071900 - Радиотехника, электроника и телекоммуникации
- •Математика 1 Пояснительная записка
- •2 Примерный перечень практических занятий
- •Учреждение «Университет «Туран»
- •Рабочая программа по дисциплине: «Математика 1»
- •Пояснительная записка
- •Общие данные по рабочей программе.
- •Общее описание рабочей программы
- •Иметь представление о роли аналитической геометрии и линейной алгебры в прикладных исследованиях;
- •Основная часть тематика лекционных занятий
- •Тематика практических занятий
- •Тематика самостоятельной работы
- •Тематика срсп
- •Список рекомендуемой литературы
- •Учреждение «Университет «Туран»
- •Силлабус по дисциплине: «Математика 1»
- •Описание изучаемой дисциплины (пояснительная записка)
- •Общие данные по рабочей программе.
- •Общее описание рабочей программы
- •Иметь представление о роли аналитической геометрии и линейной алгебры в прикладных исследованиях;
- •Темы и продолжительность их изучения
- •Тематика практических занятий
- •Задания самостоятельной работы
- •Рубежный контроль
- •Критерии оценки знаний обучающихся (обобщенные)
- •Определение итоговой оценки по вск
- •Итоговая оценка
- •Вопросы для проведения контроля
- •Требования преподавателя
- •Правила поведения на аудиторных занятиях
- •Методические указания
- •График выполнения и сдачи заданий по дисциплине
- •Учреждение «Университет «Туран»
- •1 Тема: Матрицы и определители
- •2 Тема: Система линейных уравнений.
- •3 Тема: Элементы векторной алгебры.
- •4 Тема: Аналитическая геометрия на плоскости
- •1. Различные уравнения прямой
- •1.2 Уравнение прямой, проходящей через две точки
- •1.3 Нормальное уравнение прямой
- •5 Тема: кривые второго порядка
- •6 Тема: Аналитическая геометрия в пространстве
- •7 Тема: Поверхности второго порядка
- •Глоссарий
- •Глоссарий
- •12 Тема. Дифференцирование неявных и параметрически заданных функций
- •13 Тема. Дифференциал функции
- •Глоссарий
- •План практических занятий
- •Методические рекомендации по изучению дисциплины
- •«Математика 1»
- •(По работе с учебно-методическим комплексом)
- •Основания, целевая аудитория и ориентированность учебно-методического комплекса
- •Структура, содержание и образовательные возможности учебно-методического комплекса
- •Рекомендуемый порядок работы с учебно-методическим комплексом
- •Материалы для самостоятельной работы обучающегося по дисциплине «Математика 1»
- •Тема 1. Матрицы и определители. Системы линейных алгебраических уравнений.
- •Материалы по контролю и оценке учебных достижений обучающихся
- •Карта обеспеченности дисциплины учебной и учебно-методической литературой
Глоссарий
|
№ п/п |
Новые понятия |
Содержание |
|
1 |
Функция |
Правило,
закон, по которому каждому значению
|
|
2 |
Основные элементарные функции |
|
|
3 |
Формула сложных процентов |
|
|
4 |
Предел
последовательности
|
Число
А, к которому можно приблизиться с
любой степенью точности при
|
|
5 |
Предел
функции
|
Число
А есть предел функции в т. х0,
если
|
|
6 |
Первый замечательный предел |
|
|
7 |
Второй замечательный предел |
|
|
8 |
Непрерывность
функции
|
Функция
|
10-11 тема. Дифференцирование функции.
Производной функции
![]() называется предел отношения приращения
функции к приращению независимой
переменной при стремлении последнего
к нулю (если этот предел существует)
называется предел отношения приращения
функции к приращению независимой
переменной при стремлении последнего
к нулю (если этот предел существует)
![]() .
.
Если
функция в точке
![]() имеет
конечную производную, то функция
называется дифференцируемой в этой
точке. Функция дифференцируемая в
каждой точке промежутка
имеет
конечную производную, то функция
называется дифференцируемой в этой
точке. Функция дифференцируемая в
каждой точке промежутка![]() ,
называется дифференцируемой на этом
промежутке.
,
называется дифференцируемой на этом
промежутке.
Геометрический
смысл производной: производная
![]() есть угловой коэффициент (тангенс угла
наклона) касательной, приведенной к
кривой
есть угловой коэффициент (тангенс угла
наклона) касательной, приведенной к
кривой![]() в точке
в точке![]() .
.
Тогда
уравнение касательной к кривой
![]() в точке
в точке![]() примет вид
примет вид
![]() .
.
Механический смысл
производной: производная пути по времени
![]() есть скорость точки в момент времени
есть скорость точки в момент времени![]() :
:![]()
Экономический
смысл производной: производная объема
произведенной продукции по времени
![]() есть производительность труда в момент
есть производительность труда в момент![]()
Теорема. Если
функция
![]() дифференцируема в точке
дифференцируема в точке![]() ,
то она в этой точке непрерывна.
,
то она в этой точке непрерывна.
Производная функции
![]() может быть найдена по следующей схеме
может быть найдена по следующей схеме
Дадим аргументу
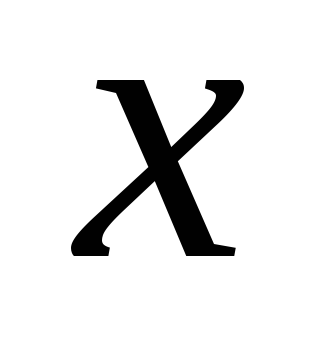 приращение
приращение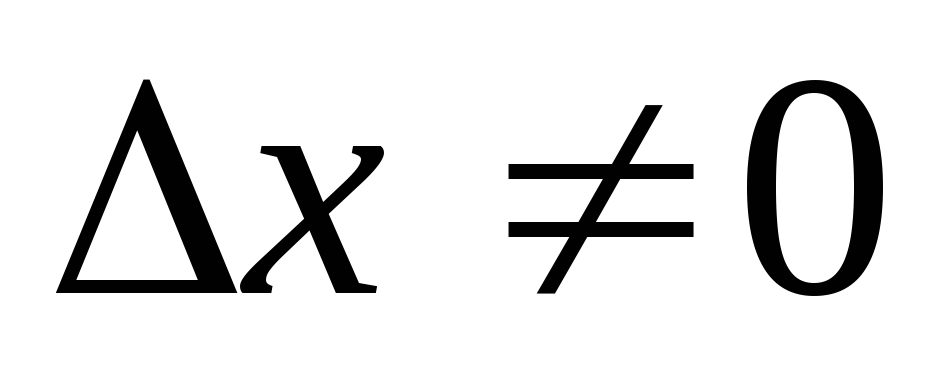 и найдем наращенное значение функции
и найдем наращенное значение функции .
.Находим приращение функции
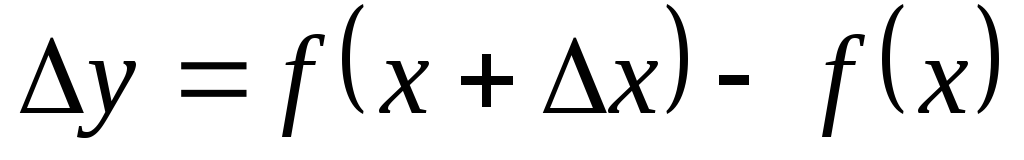 .
.Составляем отношение
 .
.Находим предел этого отношения при
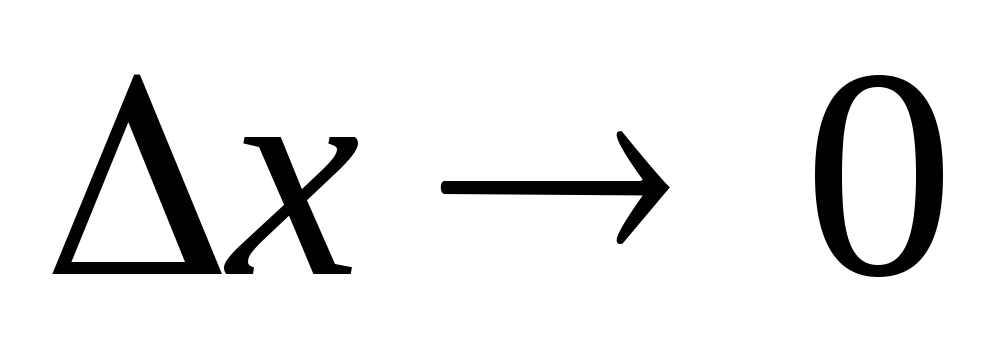 ,
то есть
,
то есть ( если этот предел существует).
( если этот предел существует).
Правила дифференцирования
Производная постоянной величины равна нулю, то есть
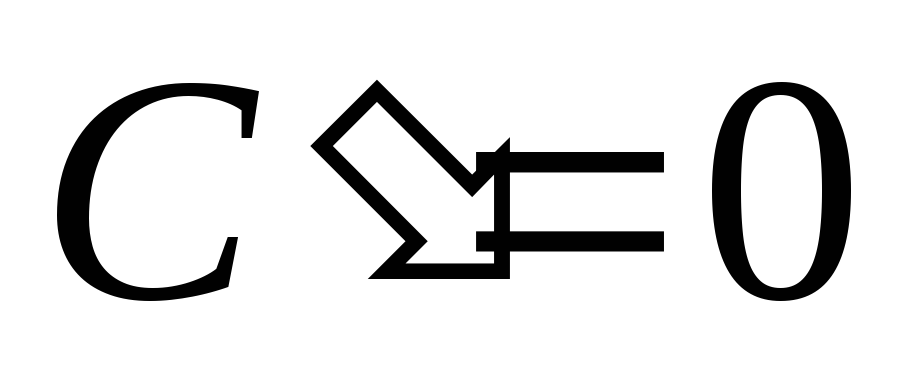 .
.Производная аргумента равна 1, то есть
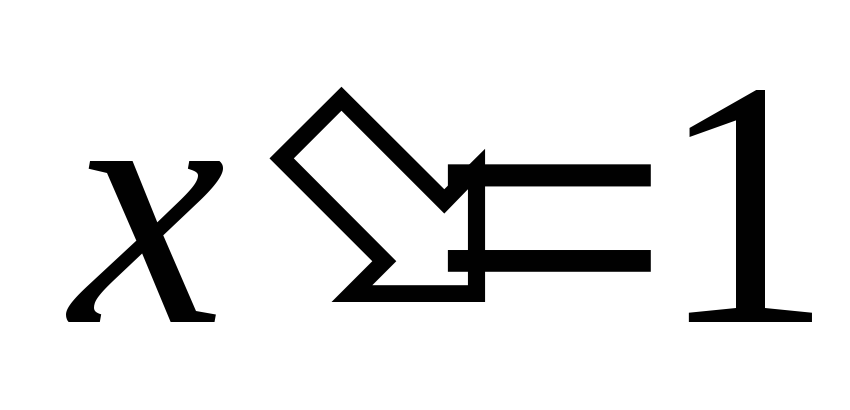 .
.Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, то есть
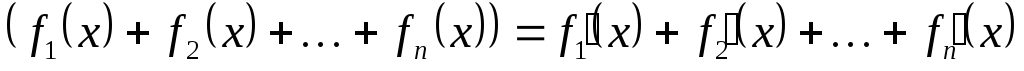 .
.Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, то есть
![]()
Производная частного двух дифференцируемых функций может быть найдена по формуле:
![]() .
.
Теорема. Если
![]() и
и![]() - дифференцируемые функции от своих
переменных, то производная сложной
функции существует и равна производной
данной функции по промежуточному
аргументу и умноженной на производную
самого промежуточного аргумента по
независимой переменной
- дифференцируемые функции от своих
переменных, то производная сложной
функции существует и равна производной
данной функции по промежуточному
аргументу и умноженной на производную
самого промежуточного аргумента по
независимой переменной![]() ,
то есть
,
то есть
![]() .
.
Теорема. Для
дифференцируемой функции с производной
не равной нулю, производная обратной
функции равна обратной величине
производной данной функции, то есть
![]() .
.
Теорема Ферма.
Если дифференцируемая на промежутке
![]() функция
функция![]() достигает наибольшего или наименьшего
значения во внутренней точке
достигает наибольшего или наименьшего
значения во внутренней точке![]() этого промежутка, то производная
функции в этой точке равна нулю, то
есть
этого промежутка, то производная
функции в этой точке равна нулю, то
есть![]() .
.
Теорема Ролля.
Пусть функция
![]() удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
непрерывна на отрезке
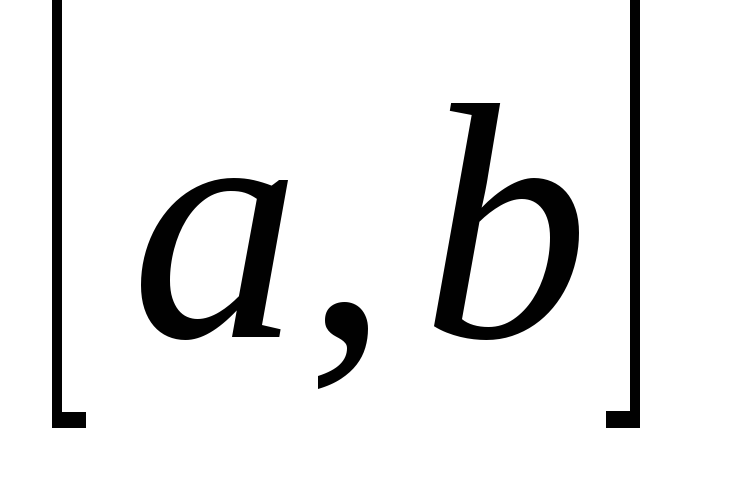 ;
;дифференцируема на интервале
 ;
;на концах отрезка принимает равные значения, то есть
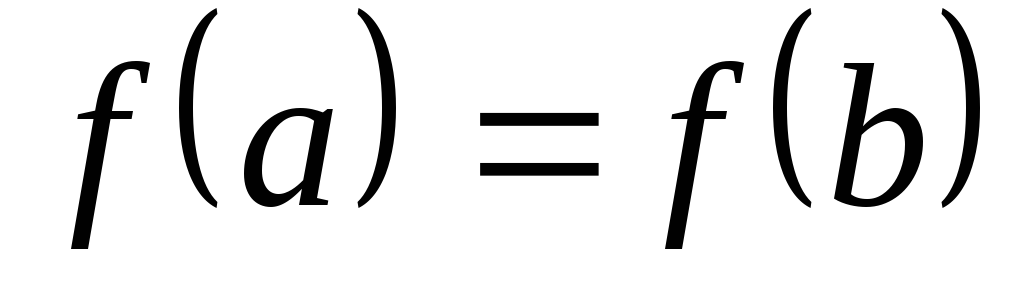 .
.
Тогда
внутри отрезка существует по крайней
мере одна такая точка
![]() ,
в которой производная функции равна
нулю:
,
в которой производная функции равна
нулю:![]() .
.
Теорема Лагранжа.
Пусть функция
![]() удовлетворяет следующим условиям
удовлетворяет следующим условиям
Непрерывна на отрезке
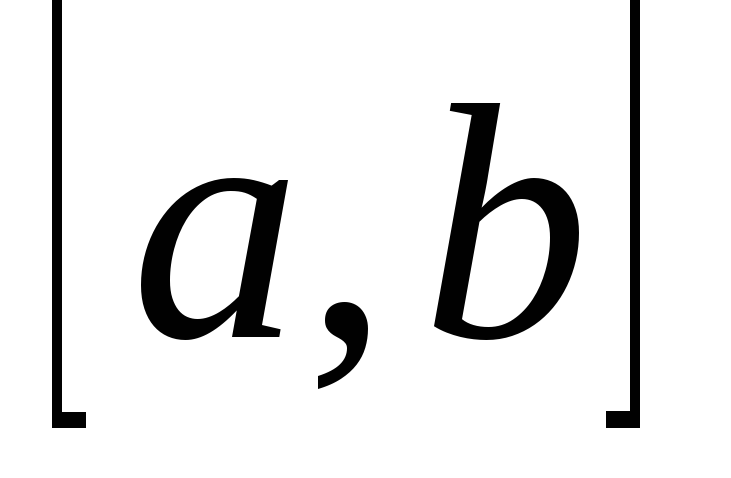 .
.дифференцируема на интервале
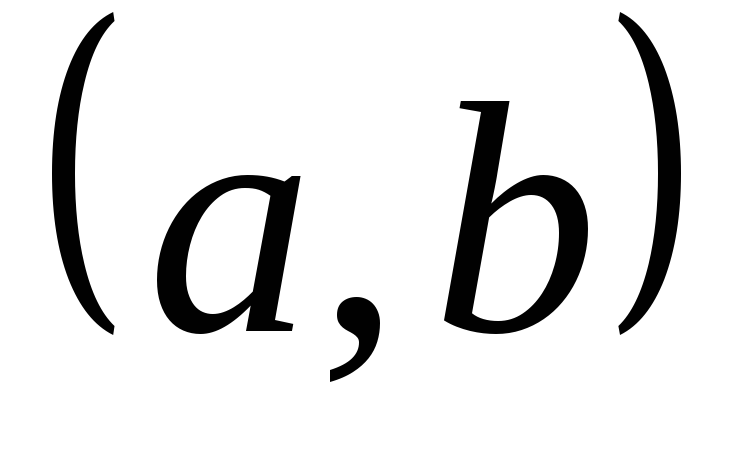 ;
;
Тогда
внутри отрезка существует по крайней
мере одна такая точка
![]() ,
в которой производная равна частному
от деления приращения функции на
приращение аргумента на этом отрезке,
то есть
,
в которой производная равна частному
от деления приращения функции на
приращение аргумента на этом отрезке,
то есть![]() .
.
Теорема Лопиталя.
Предел отношения двух бесконечно малых
или бесконечно больших функций равен
пределу отношения их производных
(конечному или бесконечному), если
последний существует в указанном смысле.
Итак, если имеется неопределенность
вида
![]() или
или![]() ,
то
,
то![]()
![]()
Дифференциалом
функции называется главная, линейная
относительно
![]() часть приращения функции, равная
произведению производной на приращение
независимой переменной:
часть приращения функции, равная
произведению производной на приращение
независимой переменной:
![]() где
где
![]()

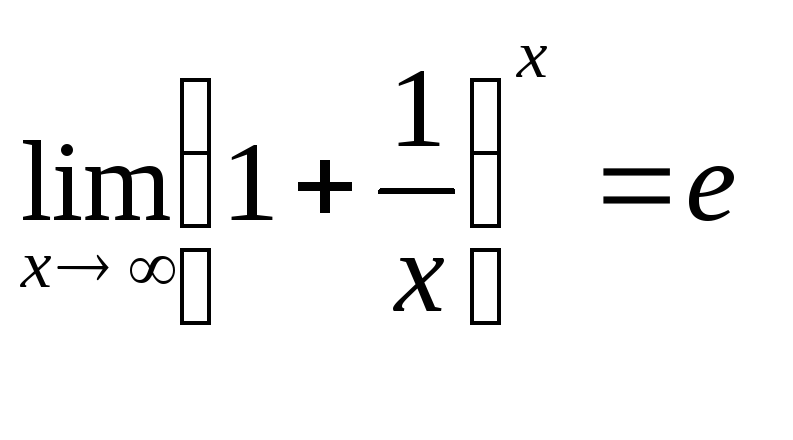 или
или