6 Тема: Аналитическая геометрия в пространстве

Общее уравнение плоскости.

В пространстве существует единственная плоскость, проходящая через заданную точку М перпендикулярная к нормальному вектору n. Уравнение этой плоскости относительно данной системы координат имеет вид:

Ax+By+Cz+D=0 (1)

Уравнение (1) называется общим уравнением плоскости.

(2)

а уравнение (2)— уравнением плоскости, проходящей через точку М (х₁ ,y₁ ,z₁) перпендикулярно к вектору п = (А, В, С).

Расстояние от точки до плоскости. Пусть даны точка М₀ (x₀, y₀, z₀) и плоскость

Аx+By+Сz+D=О. (3)

Тогда расстояние от точки до плоскости находится по формуле

(4)

Угол между двумя плоскостями находится как угол между векторами нормалями плоскостей по известной формуле

Условие параллельности и перпендикулярности двух плоскостей.

Условия паралельности имеют вид:

(5)

Если плоскости взаимно перпендикулярны, то векторы n₁ и n₂ будут также взаимно перпендикулярны, и их скалярное произведение должно быть равно нулю:

А₁A₂ + В₁B₂ + С₁C₂ = О (7)

Прямая в пространстве.

Каноническое уравнение прямой, заданной точкой М₀(x₀,y₀,z₀) и направляющим вектором имеет виді:

(8)

а векторное уравнение: (9)

параметрическое уравнение :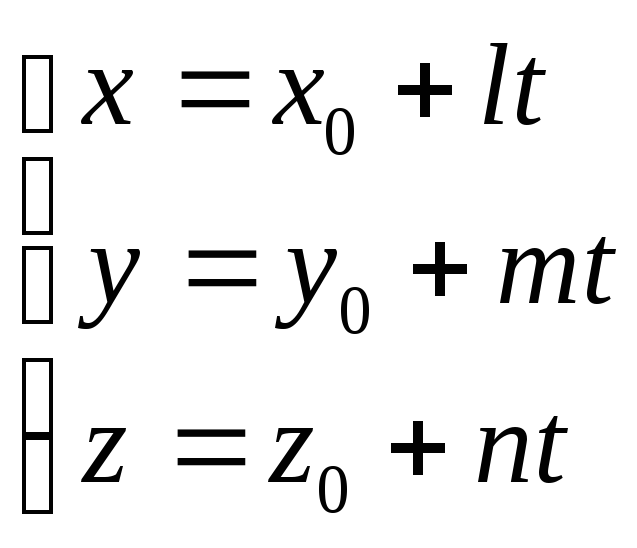(10)

Каноническое уравнение прямой проходящей через две точки

(11)

а параметрическое урвнение: (12)

Уравнение прямой заданной как пересечение двух плоскостей

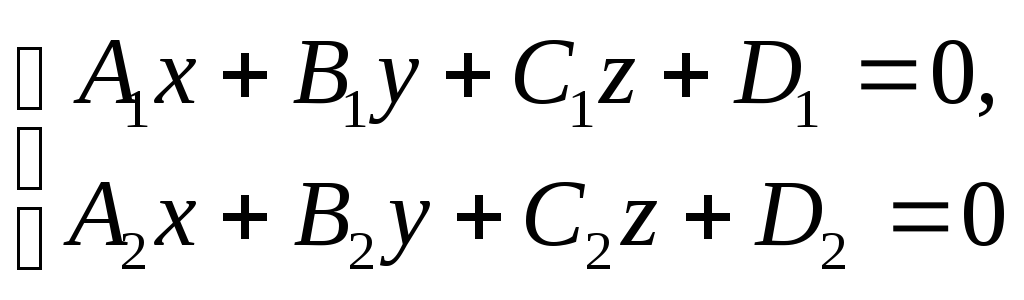(13)

Для того чтобы две прямые L₁ и L₂ в пространстве были ортогональнынеобходимо и достаточно, чтобы

, (14)

а для того чтобы они были паралельны необходимо выполнение условия (15)

7 Тема: Поверхности второго порядка

Основные понятия. Поверхность и ее уравнение. Рассмотрим фигуру Ф и введем в пространстве аффинную систему координат О е₁е₂е₃ Условие, определяющим фигуру Ф в данной системе координат, называется уравнение или неравенство(или их система), которому удовлетворяют координаты точки, не принадлежащей фигуре Ф. Уравнение, определяющее фигуру Ф, называется уравнением фигуры Ф в данной системе координат.

При изучении геометрии в пространстве методом координат в качестве фигур чаще всего рассматривают поверхности. Примерами поверхностей являются плоскость, сфера, цилиндрические и конические поверхности и др. Условием, определяющим поверхность Ф в данной системе координат, являются как правило, уравнение, которое называется уравнением поверхности Ф.

Сфера и ее уравнение. Сферой называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не больше данного, от данной точки.

(x-a)² +(у-b)²+(z-c)²=r² уравнение сферы радиуса r с центром в точке С (а,b,с).

В частности, если центр сферы совпадает с началом координат, то а=b=с=0, поэтому уравнение (1) принимает вид

x²+y²+c²=r² (1)

Уравнение (1) можно записать в виде

x²+b²+c²+Ax+By+D=0 (2)

где

А=-2а, В=-2b С=-2с, D=a²+b²+c²+r² (З)

Эллипсоид и ее каноническое уравнение. Эллипсом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

x²/a²+y²/b²+z²/c²=1

это уравнение называется каноническим уравнением эллипсоида. Положительные числа а,Ь,с называются полуосями эллипсоида.

Если аb, bс, ca то эллипсоид называется трехосным. Так как в уравнение (1) x,y,z входят только в четных степенях, то эллипсоид, заданный уравнением (1)

симметричен относительно координатных плоскостей, начала координат и осей координат. Центр симметрии эллипсоида называется его центром, а оси симметрии эллипсоида — его осями. Каждая из осей пересекает эллипсоид в двух точках, которые называются его вершинами. У трехосного эллипсоида шесть вершин: А₁(a,0,0), А₂(-а,0,0), В₁(0,b,0), B₂(0,-b,0), C₁(0,0,c), С₂(0,0,-с).

Гиперболоиды и их канонические уравнения. Различают однополостные и двуполостные гиперболоиды.

Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе коордияат определяется уравнением

x²/a²+y²/b²+z²/c ²=1 (1)

это уравнение называется каноническим уравнением однополостного гиперболоида.

Так как в уравнение (1) x,y,z входят в четных степенях, то поверхность симметрична относительно плоскостей координат, осей координат (оси поверхности) и начала координат (центр поверхности). Две оси Ох и Оу пересекают поверхность в точках А₁ (а,О,0), А₂(-a,0,0) и В₁(0,b,0), В₂(0,-b,0). Эти оси называются действительными осями однополостного гиперболоида, а указанные точки их вершинами. Третья ось симметрии (ось Оz) не имеет общих точек с однополостным гиперболоидом и называется его мнимой осью. Положительные числа а,b,с называются полуосями однополостного гиперболоида.

Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

x²/a²+y²/b²+z²/ c²=-1 (2)

это уравнение называется каноническим уравнением двуполостного гиперболоида.

Из уравнения (2) следует, что поверхность симметрична относительно плоскостей координат, осей координат (оси поверхности) и начала координат (центр поверхности). Ось Оz пересекает в двух точках С₁(0,0,c) и С₂(0,0,-c) называемых вершинами двуполостного гиперболоида; сама эта прямая называется вещественной осью. Оси симметрии Ох и Оу не имеют с поверхностью (2) общих точек и называются мнимыми осями этой поверхности. Положительные числа а,b,с называются полуосями двуполостного гиперболоида.

x²/a²+y²/b²+z²/ c²=0

Это уравнение определяет коническую поверхность, которая называется асимптотическим конусом однополостного гиперболоида (1). Вершиной этого конуса служит центр поверхности (1).

Параболоиды и их канонические уравнения. Различают эллиптические и гиперболические параболоиды.

Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

x²/a²-y²/b²=2z (3)

Это уравнение называется каноническим уравнением эллиптического параболоида.

Так как х и у входят в уравнение (1) в четных степенях, то эллиптический параболоид симметричен относительно плоскостей Охz, Оyz и относительно оси Оz (ось поверхности). Эта поверхность не симметрична относительно плоскости Оху, относительно осей Ох, Оу и начала координат.

Точка пересечения эллиптического параболоида с его осью называется вершиной. Если поверхность задана каноническим уравнением (1), то начало координат выбрано в вершине поверхности.

Если в уравнение (1) a=b, то получим уравнение поверхности в виде:

x²/a²+y²/a²=2z (2)

которая называется параболоидом вращения.

Поверхности вращения. Поверхность, которая вместе с каждой своей точкой содержит всю окружность, полученную вращением этой точки вокруг некоторой фиксированной прямой d, называется поверхностью вращения.

8-9 тема: Введение в анализ. Функция. Предел и непрерывность.

Если каждому элементу множестваставится в соответствие вполне определенный элементмножества, то говорят что на множествезадана функция. При этомназывается независимой переменной или аргументом, а- зависимой переменной, а букваобозначает закон соответствия.

Множество называется областью определения или существования функции, а множество– областью значений функции.

Существуют следующие способы задания функции

1. Аналитический способ, если функция задана формулой вида

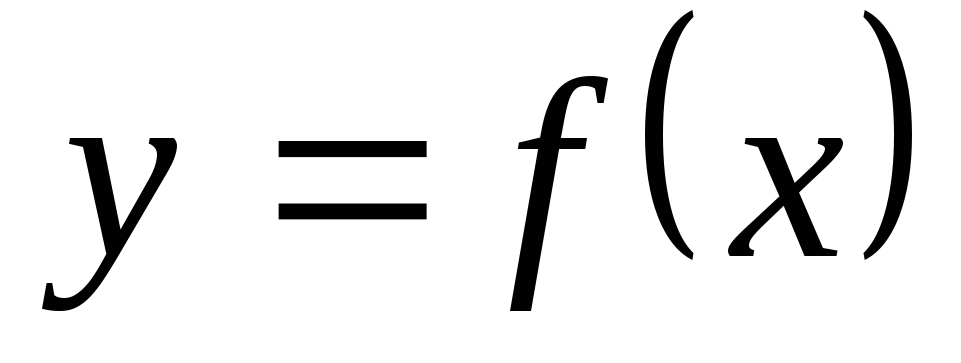
2. Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента 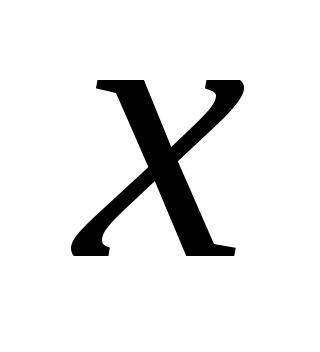и соответствующие значения функции

3. Графический способ состоит в изображении графика функции – множества точек 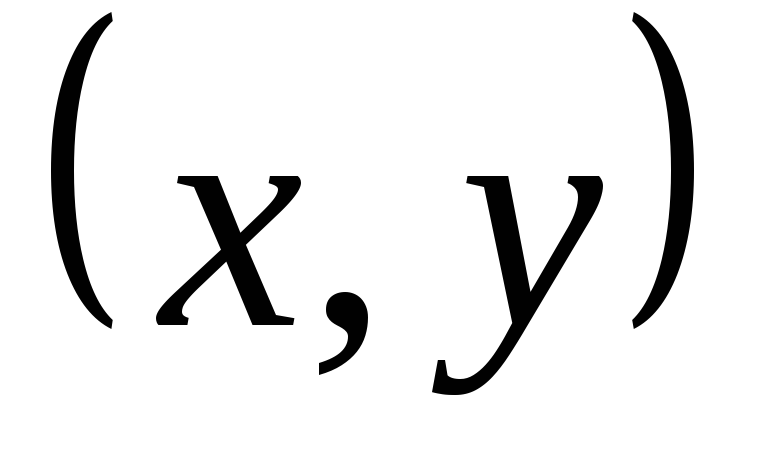плоскости, абсциссы которых есть значения аргумента 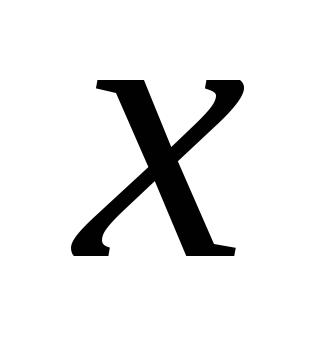, а ординаты – соответствующие им значения функции

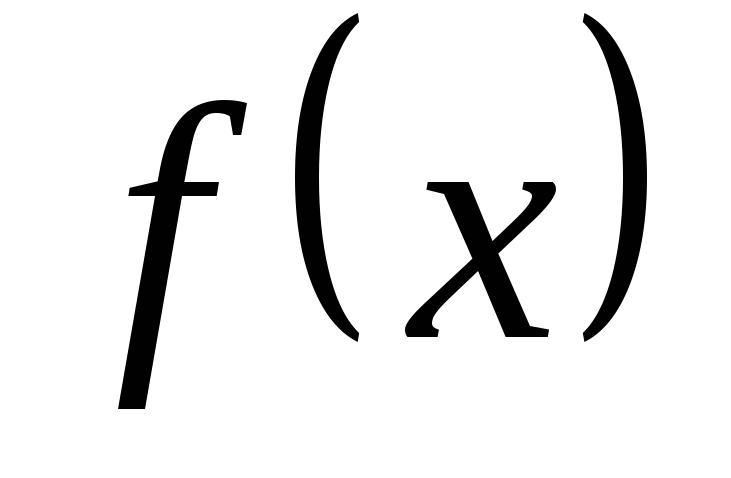
4. Словесный способ, если функция описывается правилом ее составления.

Основные свойства функции

1. Четность и нечетность. Функция называется четной, если для всех значений из области определения 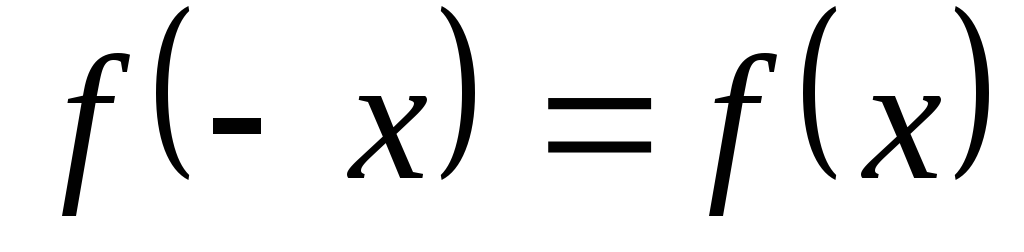и нечетной, если. В противном случае функция называется функцией общего вида.

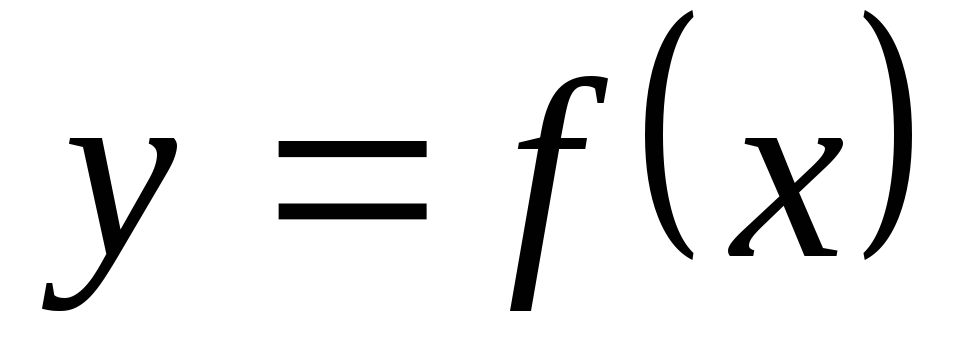2. Монотонность. Функция называется возрастающей ( убывающей ) на промежутке , если большему значению аргумента из этого пролмежутка соответствует большее ( меньшее )значение функции.

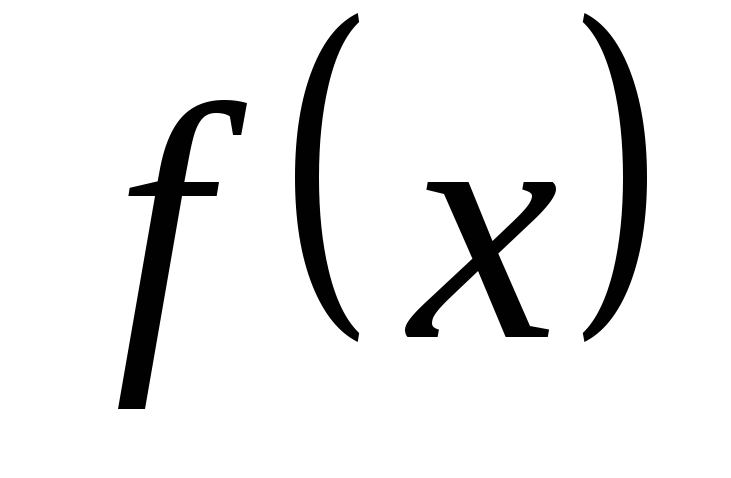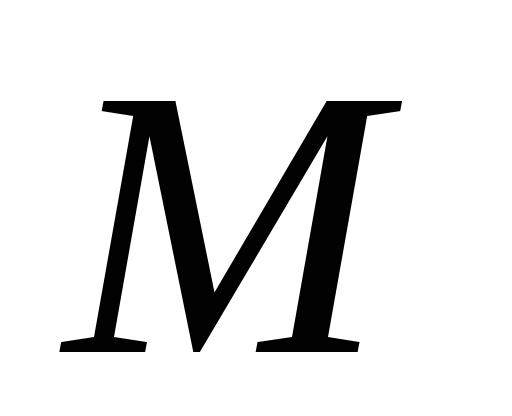3. Ограниченность. Функция называется ограниченной на промежутке , если существует такое положительное число, что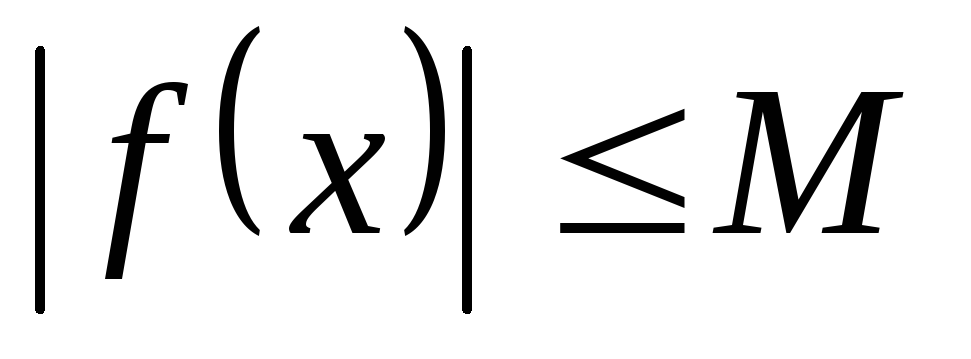для любого. В противном случае функция называется неограниченной.

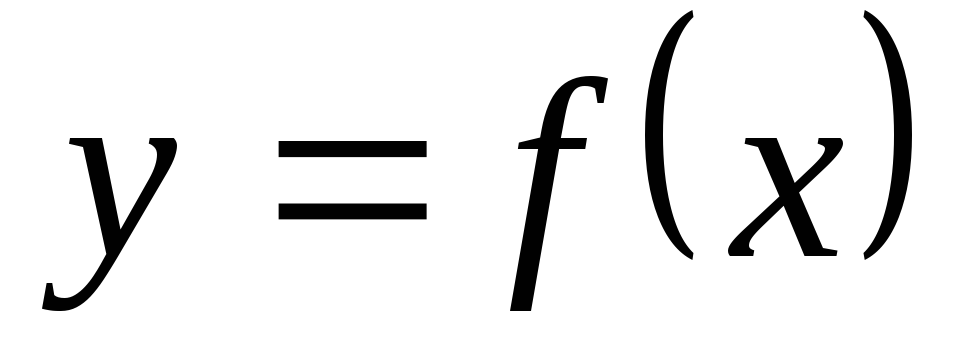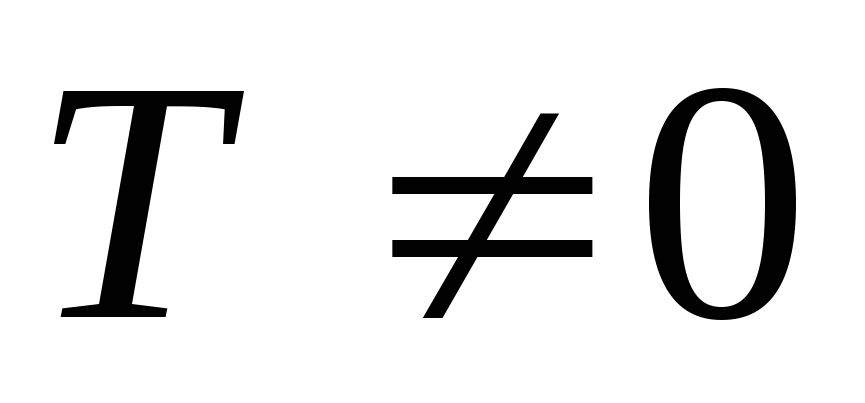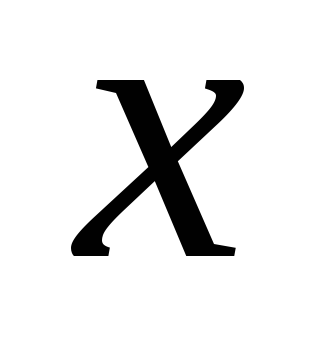4. Периодичность. Функция называется периодической с периодрм , если для любыхиз области определения функции.

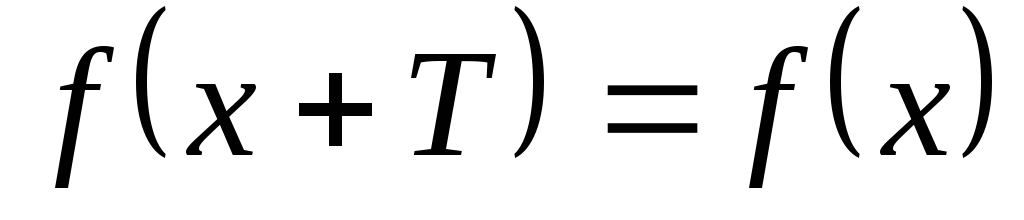Классификация функций.

1. Обратная функция. Пусть 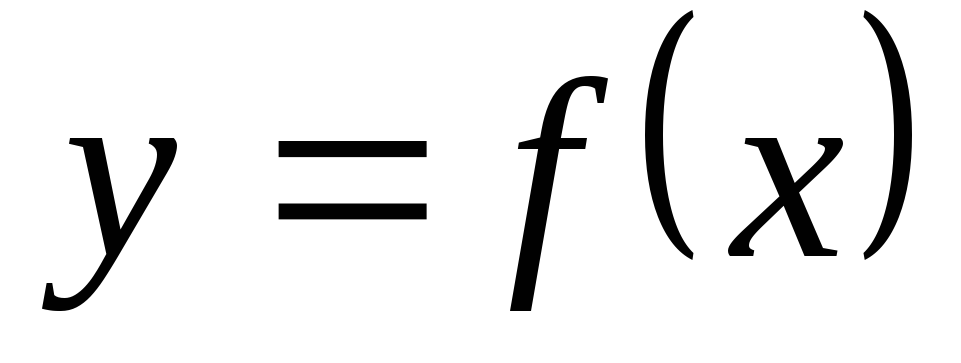есть функция от независимой переменной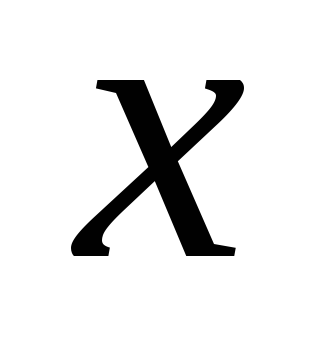, определенной на множестве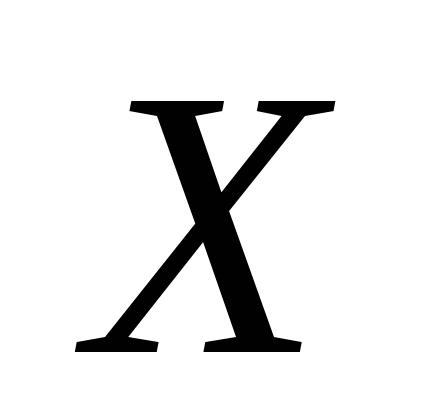с областью значений. Поставим в соответствие каждому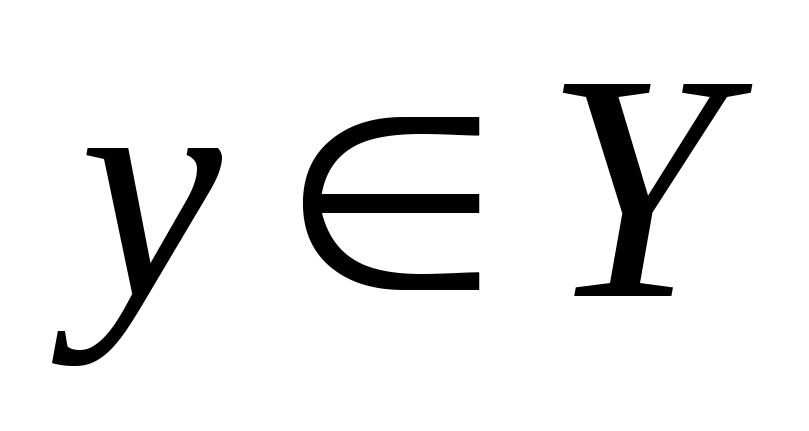единственное значение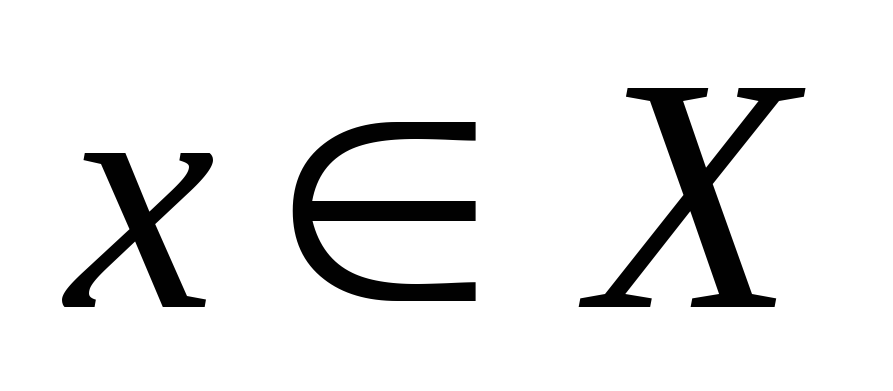, при котором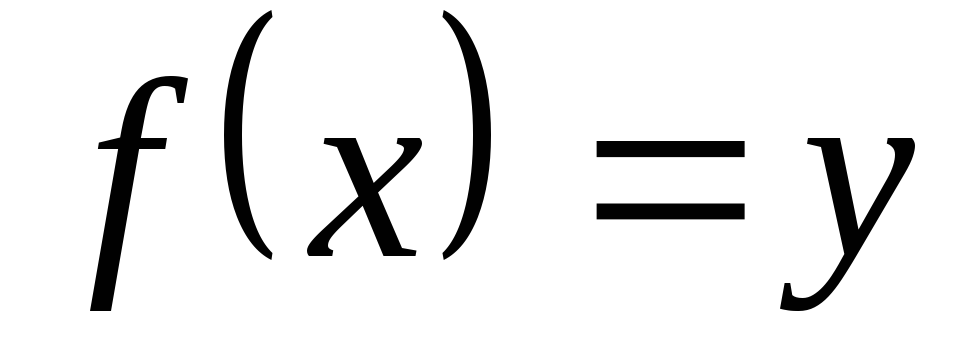. Тогда полученная функция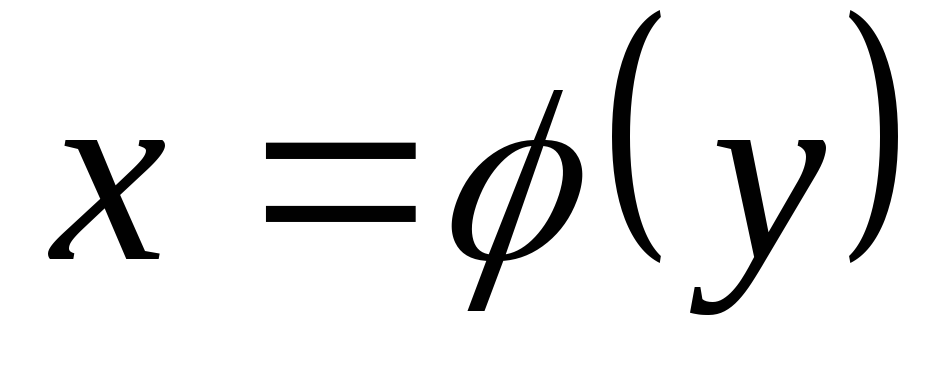, определенная на множествес областью значений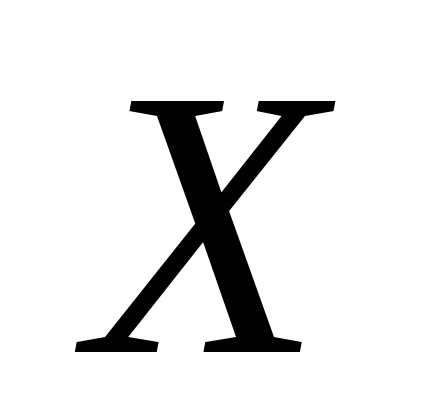называется обратной.

2. Сложная функция. Пусть функция 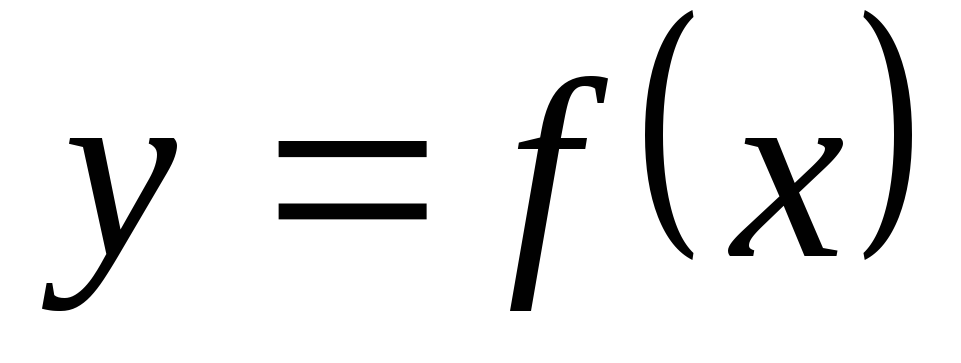есть функция от переменной, определенной на множестве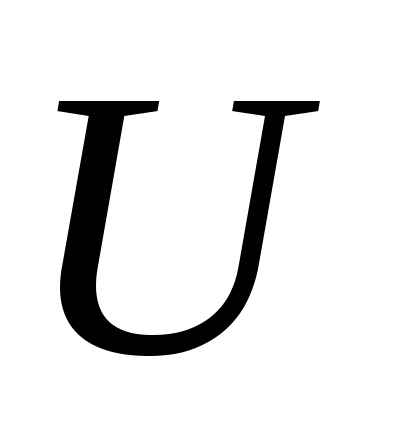 с областью значений , а переменнаяв свою очередь является функцией.

1. Числовая последовательность

Если по некоторому закону каждому натуральному числу поставлено в соответствие вполне определенное числото говорят, что задана числовая последовательность.

:

Числа называются членами последовательности, а число - общим членом последовательности.

Число называется пределом числовой последовательности, если для любого малого числанайдется такой номер(зависящий от), что для всех членов последовательности с номерамиверно равенство.Предел числовой последовательности обозначается.

Последовательность имеющая предел называется сходящейся , в противном случае – расходящейся.

Число называется пределом функциипри, если для любого малого числанайдется такое положительное число, что для всехтаких ,чтоверно неравенство.

Предел функции в точке. Пусть функция задана в некоторой окрестности точки, кроме, быть может, самой точки. Числоназывается пределом функциипри, если для любого , даже сколь угодно малого, найдется такое положительное число(зависящий от), что для всехи удовлетворяющих условиювыполняется неравенство. Этот предел обозначается.

Функция называется бесконечно малой величиной при, если ее предел равен нулю.

Свойства бесконечно малых величин

1. Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.

2. Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая

3. Частное от деления бесконечно малой величины на функцию предел которой отличен от нуля, есть величина бесконечно малая.