0. Волновая функция

Наличие у микрочастиц волновых свойств означает, что микрочастице следует сопоставить некоторое волновое поле. Амплитуда этого волнового поля зависит от координат и времени и называется волновой функцией. Волновую функцию принято обозначать с помощью символа или (в кратком варианте) просто.

Физическое толкование волновой функции было дано Максом Борном. Оно заключается в следующем.

Рассмотрим элемент объема пространства . Вероятность обнаружения частицы в объеме в момент времени будет равна

. (2.14)

Здесь - квадрат модуля волновой функции.¹

Необходимо отметить, что сама волновая функция не имеет физического смысла, смысл имеет квадрат ее модуля . Из формулы (2.14) следует, что

. (2.15)

Таким образом, квадрат модуля волновой функции есть плотность вероятности обнаружения частицы в данной точке пространства.

Вероятность нахождения частицы в ограниченной области внутри некоторого объема определится интегралом, взятым по этому объему

. (2.16)

Возьмем этот интеграл по всему пространству. Так как пребывание частицы в какой-нибудь (любой) точке пространства есть событие достоверное, то интеграл по всему пространству (в бесконечных пределах) должен быть равен 1.

(2.16)

Условие (2.16) называется условием нормировки волновой функции.

Если волновая функция известна, то средние значения физических величин, характеризующих данный микрообъект, могут быть найдены по формуле

. (2.17)

Здесь - среднее значение величины. Интегрирование производится по всей области пространства.

0. Уравнение Шредингера

Основным уравнением нерелятивистской квантовой механики является уравнение Шредингера (1926 г.). Это уравнение не выводится из каких-либо известных ранее соотношений, а является исходным основным предположением; справедливость его доказывается согласием с опытом получаемых с его помощью результатов.

Запишем его

. (2.18)

Здесь – дифференциальный оператор Лапласа;– потенциальная энергия частицы в силовом поле,m– ее масса; ;– мнимая единица.

Уравнение Шредингера дополняется условиями, которые накладываются на волновую функцию :

• волновая функция должна быть конечной, однородной, непрерывной;

• производные 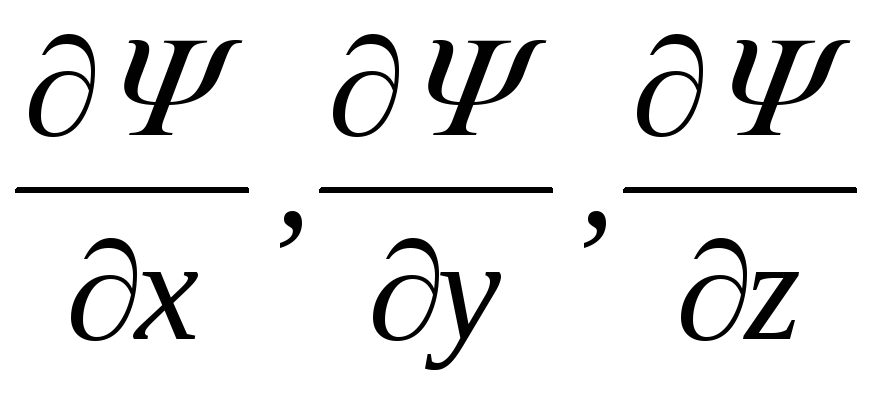должны быть непрерывны;

• интеграл 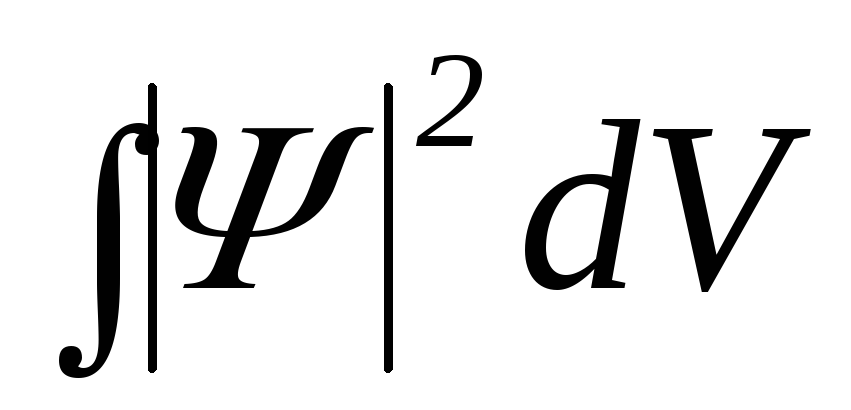должен быть конечным.

Эти условия называют стандартными условиями.

Уравнение (2.18) называется общим (временным) уравнением Шредингера. Во многих задачах квантовой механики силовое поле, в котором движется частица, стационарно. Это означает, что ее потенциальная энергия не зависит от времени и является функцией только координат, т.е. .

В этом случае волновую функцию можно представить в виде двух сомножителей

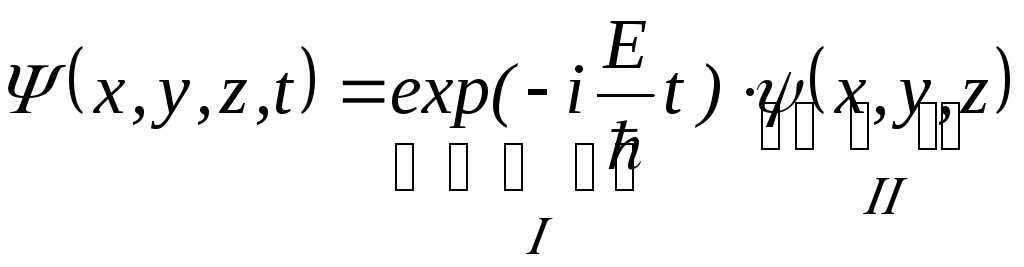(2.19 )

В этом выражении E – полная энергия частицы. Первый сомножитель зависит только от времени и называется временной частью волновой функции. Второй сомножитель зависит только от координат и называется координатной частью волновой функции.

Подставим соотношение (2.19) в уравнение Шредингера (2.18), получим:

. (2.20)

Сокращая выражение (2.20) на и преобразуя, получим:

. (2.21)

Уравнение (2.21) называется уравнением Шредингера для стационарных состояний.