Контрольні запитання

1. Сформулювати і довести теорему про першу важливу границю.

2. Сформулювати і довести теорему про другу важливу границю.

3. Дати означення функції, неперервної в точці, на відрізку, на інтервалі.

4. Що таке приріст аргументу, приріст функції?

5. Сформулюйте теорему про неперервність суми, різниці, добутку та частки двох неперервних функцій.

6. Сформулюйте теорему про неперервність складеної функції.

7. Сформулювати критерій неперервності функції.

8. Дати означення точки розриву першого та другого роду, точки усувного розриву, стрибка функції.

9. Сформулювати властивості функцій, неперервних на відрізку.

Розділ 4. Диференціальне числення функції однієї змінної

Тема 11. Диференційовність функції однієї змінної

Мета. Розширити поняття диференційовності функції однієї змінної, дати поняття диференціала та його зв’язку з похідною.

План.

1. Похідна функції, її зміст в різних задачах.

2. Необхідна умова диференційовності.

3. Основні правила диференціювання.

4. Метод логарифмічного диференціювання.

1. Розглянемо наступні задачі

а) Нехай дано криву АВ і точку М₀ , яка цій кривій належить. Візьмемо довільну точку М цієї ж кривої і проведемо пряму ММ₀. Пряма, що проходить через дві точки кривої називається січною. Січна з кривою можуть мати дві або більше спільних точок. Нехай точка М рухається вздовж кривої до точки М₀, тоді січна рухається до якогось свого граничного положення М₀Т і така пряма, яка є граничним положенням називається дотичною.

Означення: Дотичною до кривої L в точці М₀ називається граничне положення січної ММ₀, якщо точка М прямує до точки М₀ вздовж кривої.

Дотична з кривою мають одну спільну точку в деякому околі.

О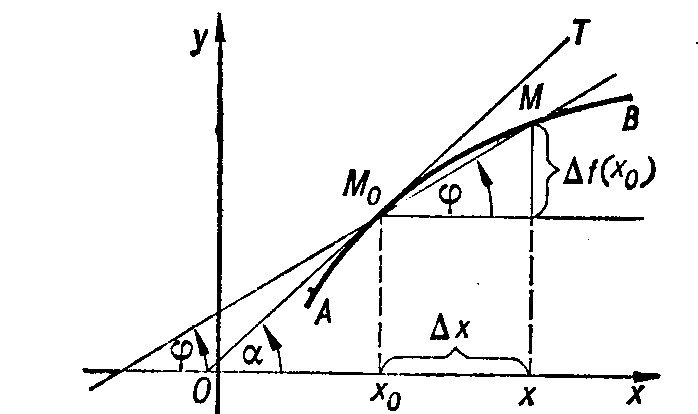бчислимо кутовий коефіцієнт дотичної до графіка функціїy=f(x).

k=tg a, де a– кут нахилу дотичної до осі Ох.

Тоді tg= , але приМ®М₀ справедливо Dх®0, а сам кутовий коефіцієнт логічно шукати як

k==.

б) Нехай деяке тіло рухається прямолінійно за заданим законом s=f(t). Тоді за час Dt тіло пройшло відстань Ds, а – середня швидкість тіла на цьому проміжку.

Означення: Швидкістю тіла в кожен конкретний момент часу t називають границю середньої швидкості тіла на цьому проміжку, при умові, що Dt прямує до 0. Тобто

.

в) Розглянемо задачу про обчислення сили змінного струму.

Нехай Q=f(t) – кількість електрики, що проходить за час t. Сила струму – це кількість електрики, що проходить через поперечний переріз за час t. За проміжок часу Dt пройде DQ струму. – середня сила струму за часDt. А в кожен конкретний момент .

Ці всі задачі приводять нас до необхідності обрахування границі відношення приросту функції до приросту аргумента, якщо приріст аргумента прямує до нуля.

Нехай функція y=f(x) визначена в точці х₀. Надамо їй приросту так, щоб х₀+Dх належала області визначення і знайдемо приріст функції в цій точці. Dy=f(x₀+Dx) – f(x₀).

Похідною функції f(x) в точці х₀ називається границя відношення приросту функції Dy до приросту аргументу Dх , якщо приріст аргумента прямує до нуля довільним способом.

Позначають .

Або .

Існують також позначення ,.

Фізичним змістом похідної є розв’язок задачі про швидкість тіла (позначають .

Геометричним змістом похідної є розв’язок задачі про знаходження кутового коефіцієнта дотичної до кривої (позначаємо ).

2. Означення 1. Функція f(x) називається диференційовною в точці х₀, якщо вона має похідну в цій точці.

Означення 2. Функція f(x) називається диференційовною в деякому інтервалі, якщо вона має похідну в кожній точці цього інтервалу.

Теорема (необхідна ознака диференційовності функції): Якщо функція y=f(x) диференційовна в точці х, то вона неперервна в цій точці.

Обернена теорема взагалі кажучи не справджується. Тобто існують неперервні функції, які в окремих точках не мають похідних. Прикладом такої функції може бути .

3. Теорема 1. Якщо функції f(x) і j(х) диференційовні в точці х, то в цій точці диференційовна функція f(x) + j(х), причому

,

тобто похідна суми диференційованих в точці х функцій дорівнює сумі похідних цих функцій в розглядуваній точці.

Теорема 2. Якщо функції f(x) і j(х) диференційовні в точці х, то в цій точці диференційовна функція f(x)j(х), причому

,

тобто похідна добутку диференційовних в точці х функцій дорівнює сумі похідної першої з цих функцій в розглядуваній точці на другу функцію без зміни плюс похідну другої з цих функцій в розглядуваній точці на першу функцію без зміни .

Лема. Якщо f(x)=c, де с – стала для хÎ(a, b), то , тобто похідна сталої функції дорівнює нулю.

Наслідок 1. Якщо функція f(x) диференційовна в точці х, то функція cf(x), де с– стале число є диференційовною , причому

,

тобто сталий множник можна винести за знак похідною.

Наслідок 2.Різниця двох функцій, диференційованих в точці х є функція, диференційована у точці х, причому

.

Теорема 3. Якщо функції f(x) і j(х) диференційовні в точці х, причому в цій точці j(х)¹0, то в цій точці диференційовна функція f(x)/j(х), причому

.

Наслідок 3. Якщо функція j(х) диференційовна в точці х, причому в цій точці j(х)¹0, то в цій точці диференційовна функція , причому

.

Теорема 4. Справедливі наступні рівності:

4. Якщо потрібно продиференціювати функцію , задану у вигляді дробу, добутку чи у вигляді степеневої функції, основою і показником якої є функції незалежного аргументу вигідно спочатку прологарифмувати обидві частини функції за основою е, а вже потім диференціювати. Цей прийом має назву логарифмічного диференціювання. Похідна від логарифму називається логарифмічною похідною. До цього засобу зручно звертатися і тоді, коли ми маємо функцію, що містить корені з дробів. І до нього завжди звертаються, коли необхідно продиференціювати функцію вигляду

Розглянемо цей спосіб на прикладі:

Знайти похідну функції .

Розв’язування:

Прологарифмуємо обидві чатини рівності

.

Вважаючи, що lny є складеною функцією від х і диференціюючи обидві частини рівності , маємо

.

Множимо обидві частини рівності на , отримуємо, що шукана похідна має вигляд

.

Після очевидних спрощень отримаємо: .