Розв’язування. В силу симетрії кривої визначаєм спочатку одну чверть шуканої площі

.

Звідси S=a².

Довжина дуги в прямокутних координатах.

Довжина дуги гладкої кривої y=f(x), яка міститься між двома точками з абсцисами х=а і х=b, рівна

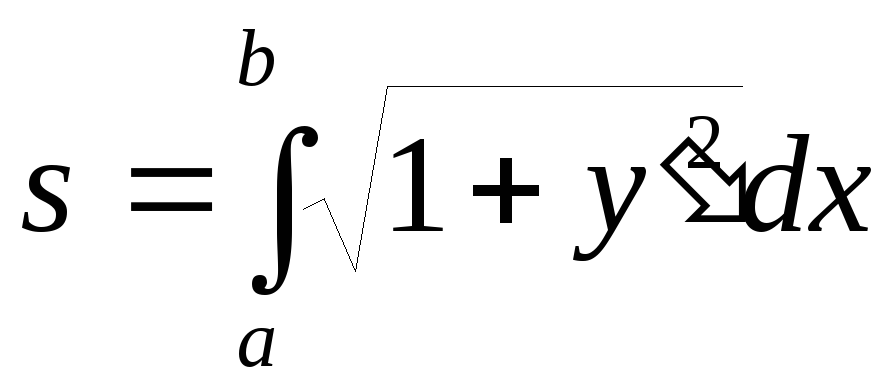. (5)

Приклад.

Знайти довжину астроїди х^2/3+у^2/3=а^2/3.

Розв’язування.

Диференціюючи рівняння астроїди, одержим:

.

Тому для довжини дуги одної чверті астроїди маємо:

.

Звідси s=6a.

Довжина дуги кривої, заданої параметрично.

Якщо крива задана рівняннями в параметричній формі х=(t) i y=(t) ((t) i =(t) – неперервно диференційовні функції), то довжина дуги s кривої рівна

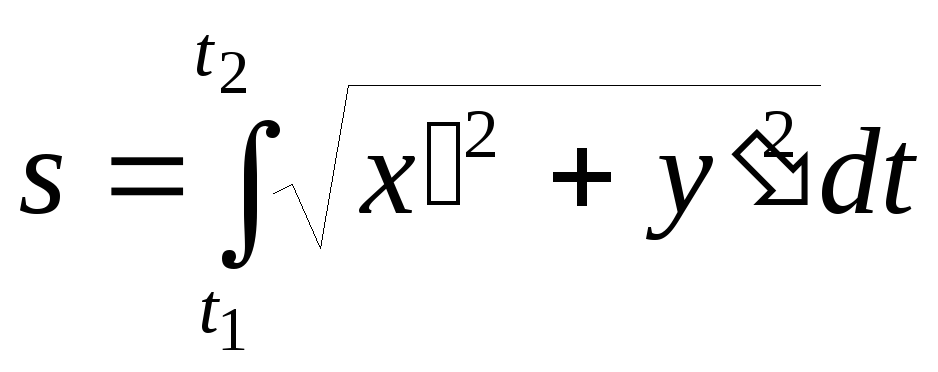, (6)

де t₁ i t₂ – значення параметра, які відповідають кінцям дуги.

Якщо гладка крива задана рівнянням r=f() в полярних координатах r і , то довжина дуги s рівна

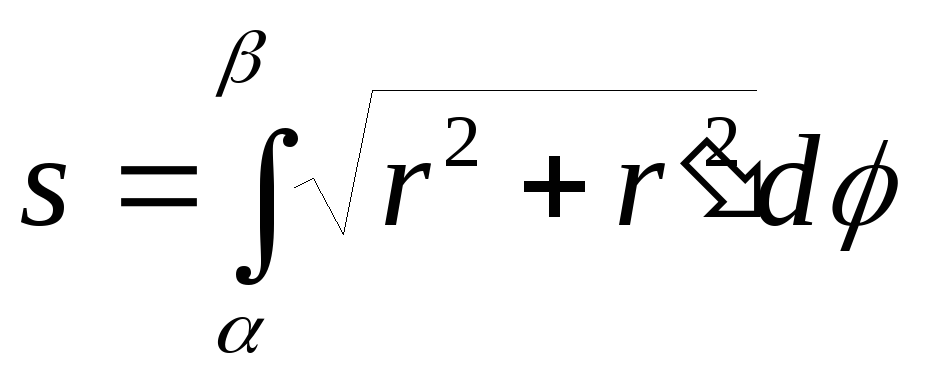, (7)

де  і  - значення полярного кута в крайніх точках дуги.

Об’єм тіла обертання.

Об’єми тіл, утворених обертанням криволінійної трапеції, обмеженої кривою у=f(x), віссю ОХ і двома вертикалями х=а і x=b, навколо осей ОХ і ОY, виражаються відповідно формулами:

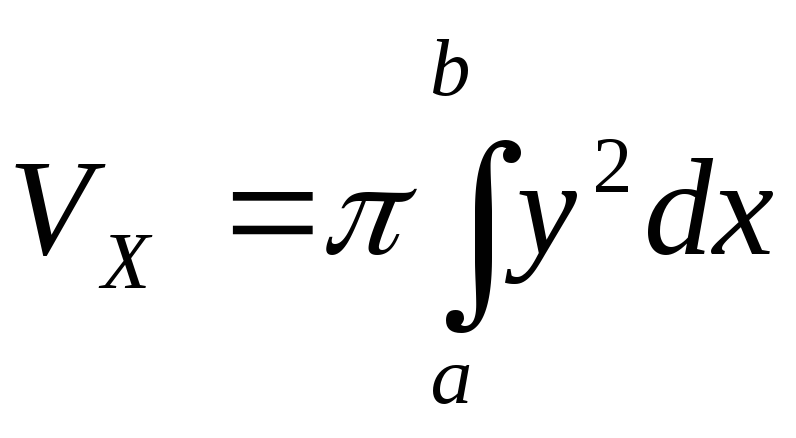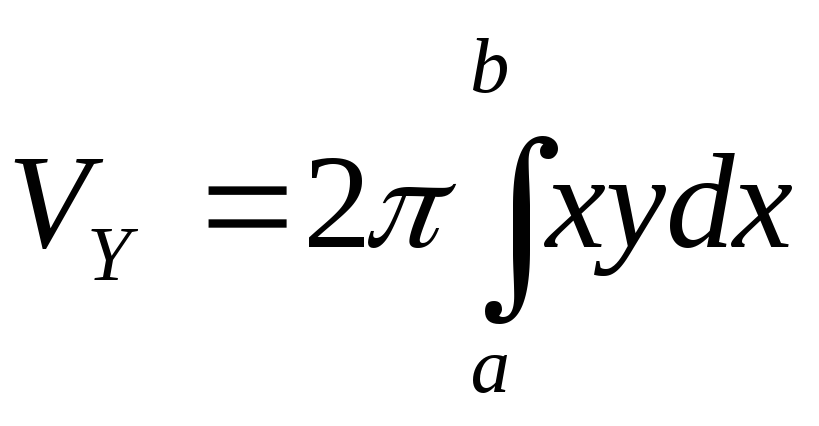1. ; 2) . (8)

Приклад.

Обчислити об’єми тіл, утворених обертаням фігури, обмеженої однією напівхвилею синусоїди у=sinx і відрізком 0х осі ОХ навколо:

а) осі ОХ і б) осі OY.

1. ;

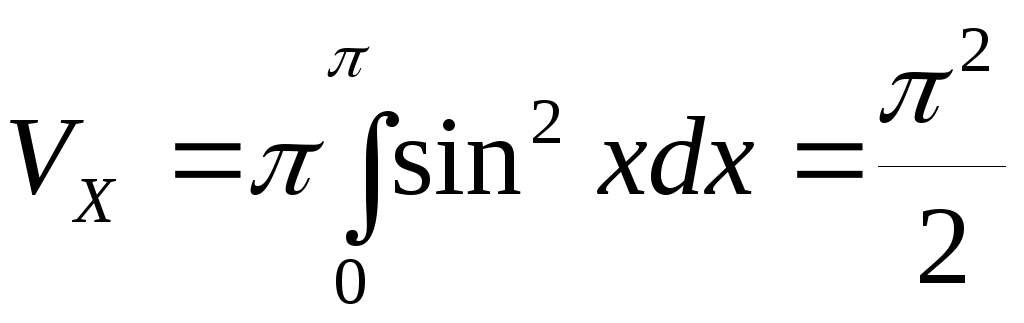б) .

Об’єм тіла, утвореного обертанням навколо осі ОY фігури, обмеженої кривою х=g(y), віссю OY і двома паралелями у=с і у=d, можна визначати по формулі:

,

яка одержується із приведеної вище формули 1)(8) шляхом перестановки координат х і у.

Якщо крива задана в іншій формі (параметрично, в полярних координатах і т.д.), то в приведених формулах потрібно зробити відповідну заміну змінної інтегрування.

В більш загальному випадку об’єми тіл, утворених обертанням фігури, обмеженої кривими у₁=f₁(x) i y₂=f₂(x) (причому f₁(x)f₂(x)) і прямими х=а, х=b, навколо координатних осей ОХ і ОY, відповідно рівні

,

.

Об’єм тіла, одержаного при обертанні сектора, обмеженого дугою кривої r=F() і двома полярними радіусами =, =, навколо полярної осі, може бути обчислений за формулою

. (9)

Цією ж формулою зручно кристуватися при знаходженні об’єму тіла, одержаного обертанням навколо полярної осі фігури, обмеженої деякою замкнутою кривою, заданою в полярних координатах.

Обчислення об’ємів тіл по відомих поперечних перерізах.

Якщо S=S(x) – площа перерізу тіла площиною, перпендикулярною до деякої прямої (яку приймаєм за вісь ОХ), в точці з абсцисою х, то об’єм цього тіла рівний

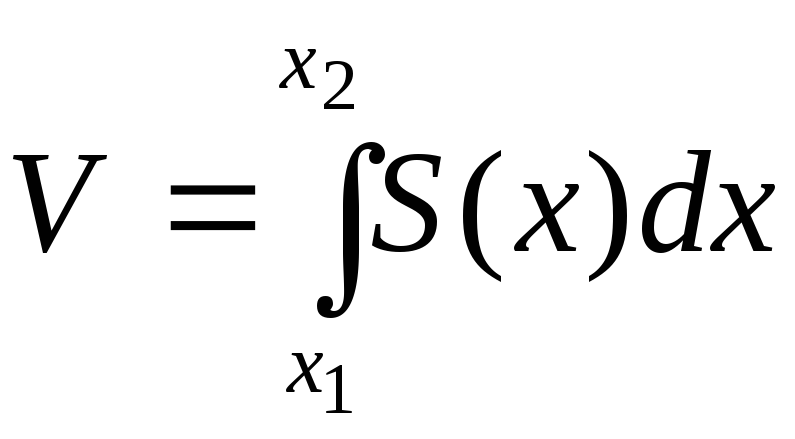, (10)

де х₁ і х₂ – обсциси крайніх перерерізів тіла.

Площа поверхні обертання.

Площа поверхні, утвореної обертанням навколо осі ОХ дуги гладкої кривої у=f(x) між точками х=а і х=b, виражається формулою

(11)

(ds – диференціал дуги кривої).

У випадку іншого задання рівняння кривої, площа поверхні S_X одержується з формули (10) шляхом відповідної заміни змінних.

Приклад.

Знайти площу поверхні, утвореної обертанням навколо осі ОХ вузла кривої 9у²=х(3-х)².

Розв’язування.

Для верхньої частини кривої при 0х3 маємо: . Звідси диференціал дуги. На основі формули (1) площа поверхні

.

2. Наведемо приклади застосування визначеного інтегралу для розв’язування деяких задач фізики.

Статичний момент.

Статичним моментом відносно осі l матеріальної точки А, які мають масу m і віддалені від осі l на відстань d, називається величина М_l=md.

Статичним моментом відносно осі l системи n матеріальних точок з масами m₁, m₂,…,m_n, які лежать в одній площині з віссю і віддалені від неї на відстані d₁, d₂, …, d_n , називається сума

(1)

причому відстані точок, які лежать по один бік осі l, беруться зі знаком плюс (+), а по інший – зі знаком мінус (-). Аналогічно визначається статичний момент системи точок відносно площини.

Якщо маси неперервно заповнюють лінію чи фігуру площини ХОY, то статичні моменти М_Х і М_Y відносно координатних осей ОХ і OY замість сум (1) виражаються відповідними інтегралами. Для випадку геометричних фігур густина вважається рівною одиниці.

А саме:

1) для кривої х=х(s); y=y(s), де параметр s - довжина дуги, маємо:

;(2)

(- диференціал дуги);

2. для плоскої фігури, обмеженої кривою у=у(х), віссю ОХ і двома вертикалями х=а і у=b, одержимо:

; (3)

Приклад.

Знайти статичні моменти відносно осей ОХ і OY трикутника, обмеженого прямими: ,х=0, у=0.

Розв’язання.

Тут. Застосовуючи формули (3), одержимо:

;

.

Момент інерції.

Моментом інерції відносно осі l матеріальної точки маси m, віддаленої від осі l на відстань d, називається число І_l=md².

Моментом інерції відносно осі l системи n матеріальних точок з масами m₁,m₂,…, m_n називається сума

, (4)

де d₁,d₂,…, d_n – відстань точок від осі l. У випадку суцільної маси замість суми одержимо відповідний інтеграл.

Приклад.

Знайти момент інерції трикутника з основою b і висотою h відносно його основи.

Розв’язання.

Основу трикуника приймаємо за вісь ОХ, а його висоту – за вісь OY.

Розіб’єм трикутник на нескінечно тонкі горизонтальні смужки товщиною dy, які відіграють роль елементарних мас dm.

Тоді:

і

.

Звідси

.

Центр тяжіння.

Координати центра тяжіння плоскої фігури (дуги чи площини) маси М обчислюються за формулами:

, , (5)

де М_Х і М_Y – статичні моменти тіла. У випадку геометричних фігур маса М чисельно рівна відповідній дузі чи площі.

Для координат центра тяжіння () дуги плоскої кривоїy=f(x) (axb), яка сполучає точки А(а; f(a)) i B(b; f(b)), маємо:

, .

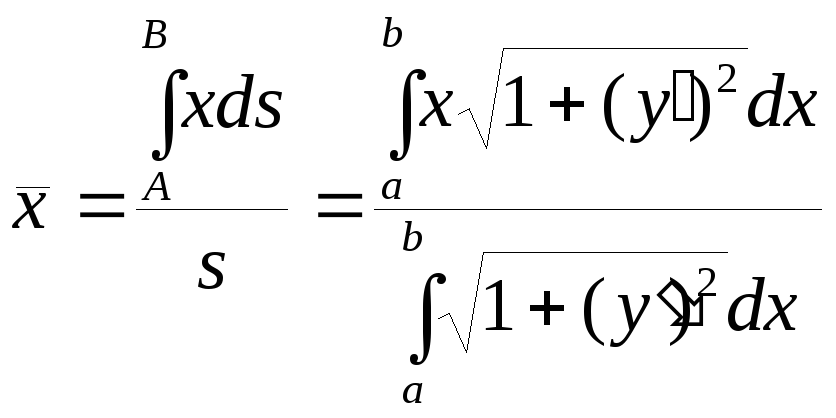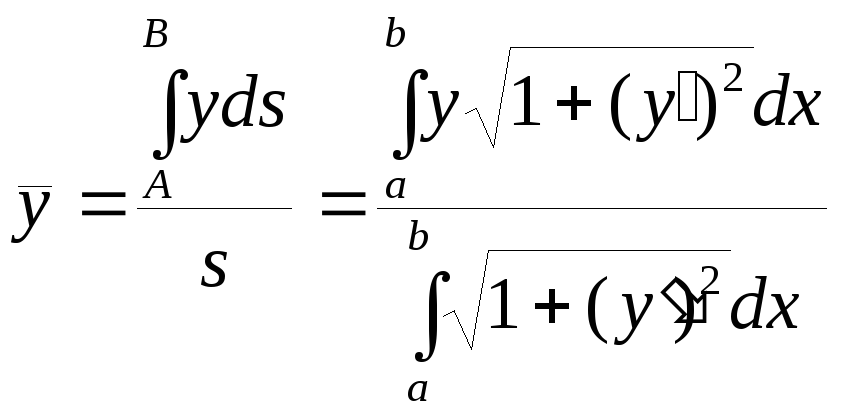Координати центра тяжіння () криволінійної трапеціїaxb, 0уf(x), можуть бути обчислені за формулами:

, ,

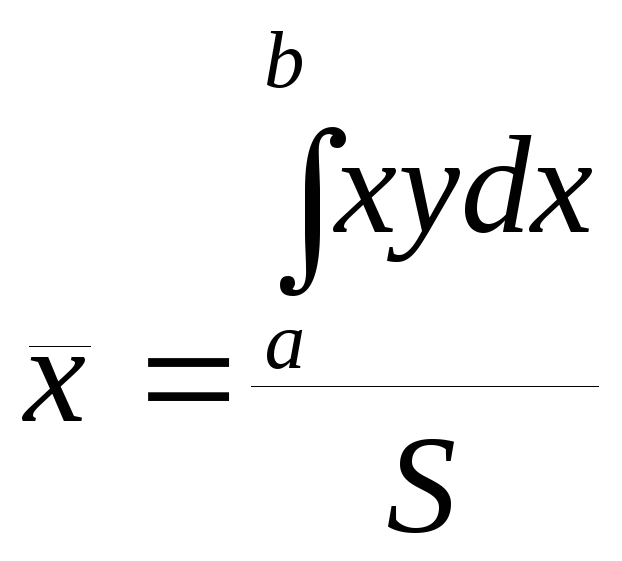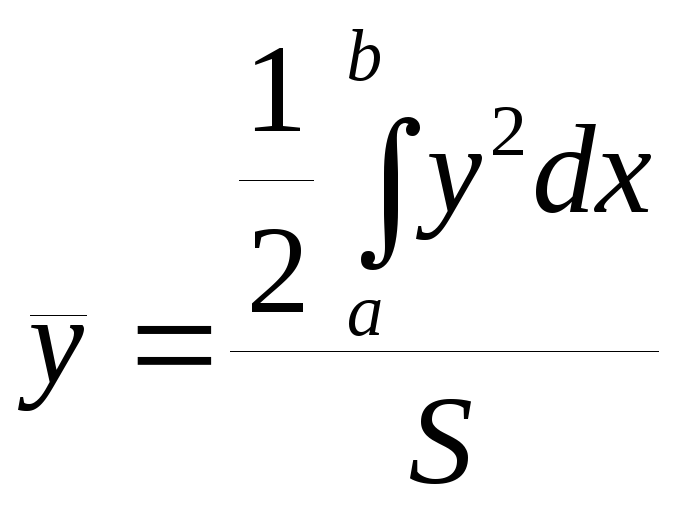де - площа фігури.

Шлях, пройдений точкою.

Якщо точка рухається по деякій кривій і абсолютна величина швидкості її v=f(t) є відома функція часу t, то шлях, пройдений точкою за проміжок часу [t₁, t₂], рівний

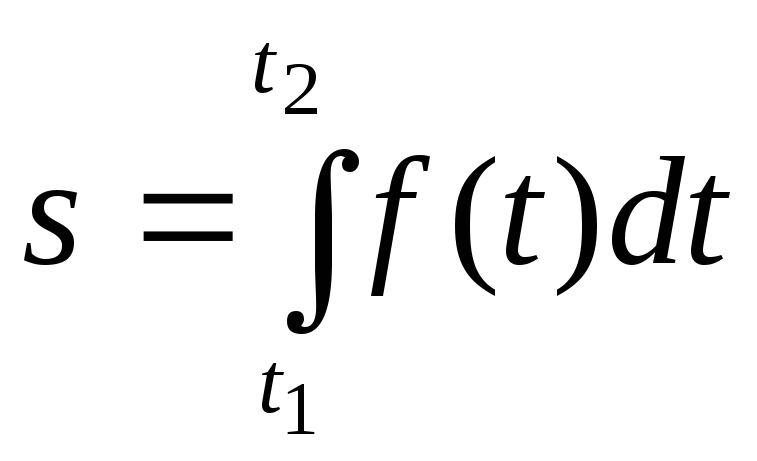. (6)

Приклад.

Швидкість точки рівна v=0,1t³ , м/сек. Знайти шлях s, пройдений точкою за проміжок часу Т=10 сек, яки пройшов від початку руху. Чому рівна середня швидкість руху за цей проміжок?

Розв’язування.

Маємо:

і

Робота сили.

Якщо змінна сила Х=f(x) діє в напрямку осі ОХ, то робота сили на відрізку [x₁, x₂] рівна

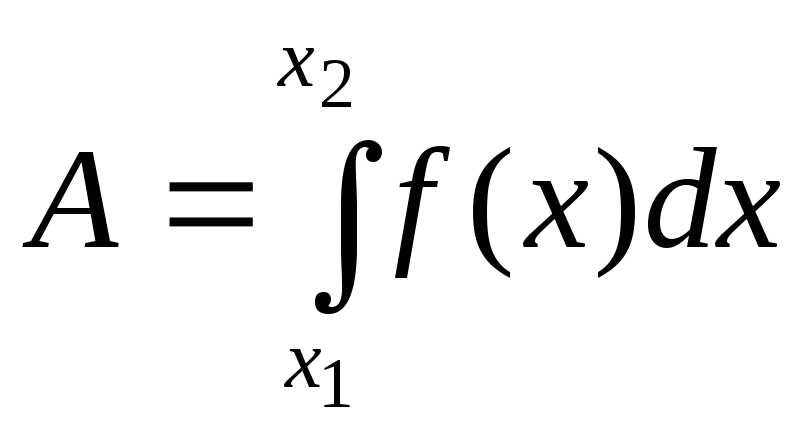. (7)

Приклад.

Яку роботу потрібно затратити, щоб розтягнути пружину на 6 см, якщо сила 1 кГ розтягує її на 1 см?

Розв’язування.

Згідно закону Гука сила Х кГ, яка розтягує пружину на х_м, рівна Х=kx, де k – коефіцієнт пропорційності.

Нехай х=0,01 м і Х=1 кГ, одержимо k=100 і, значить, Х=100х.

Звідси шукана робота рівна

кГм.