Контрольні запитання

1. Що називається матрицею, одиничною, прямокутною, квадратною матрицею?

2. Що таке транспонована матриця?

3. Які дії можна виконувати над матрицями та які їх властивості?

4. Що називається визначником другого, третього порядку?

5. Які властивості визначників?

6. Що називається мінором матриці, як можна розкласти визначник через мінори?

7. Як понизити порядок визначника?

8. Що називається оберненою матрицею, як її знайти?

9. Що називається рангом матриці?

10. Що таке лінійна залежність та лінійна незалежність рядків матриці?

Тема 2. Системи лінійних рівнянь

Мета. Навчитися розв’язувати системи лінійних рівнянь різними способами.

План.

1. Поняття про систему лінійних рівнянь.

2. Матричний спосіб розв’язування систем лінійних рівнянь.

3. Формули Крамера та їх застосування для розв’язування систем лінійних рівнянь.

4. Метод Гаусса розв’язування систем лінійних рівнянь.

1. Система m лінійних рівнянь з n невідомими має такий вигляд:

(1)

В данній системі можна виділити три матриці :

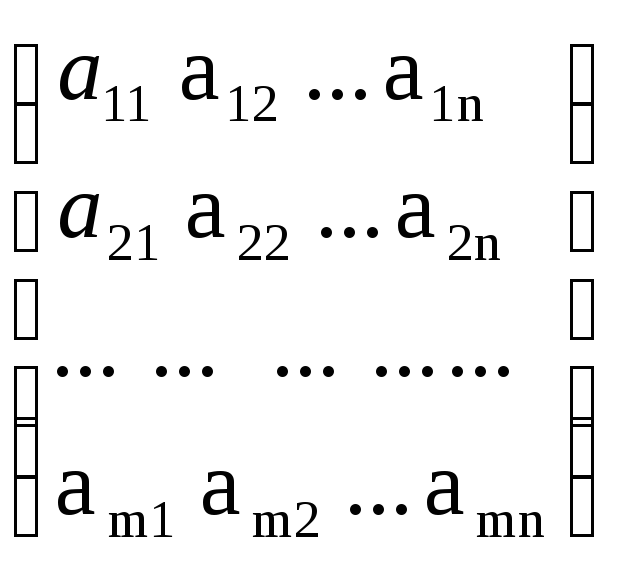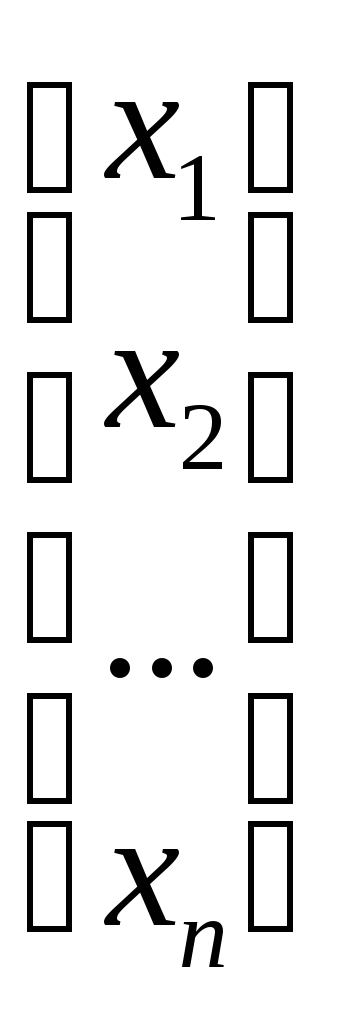А=- матриця системи; Х=; В=.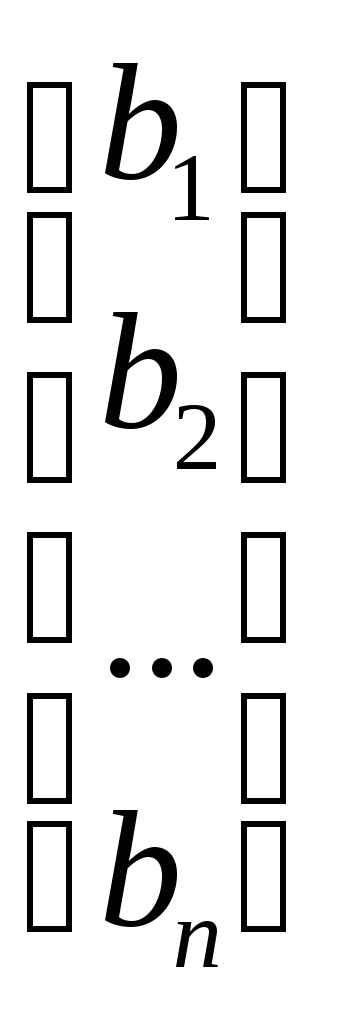

АХ=В. (2)

Роз’язком системи (1) називається деяка сукупність n чисел x₁=a₁, x₂=a₂, ... , x_n=a_n, які всі системи перетворюють у тотожність.

Якщо система має єдиний розвязок, то вона називається визначеною.

Якщо система має безліч розвязків, то вона називається невизначеною.

Система називається сумісною, якщо вона має хоч один розв’язок.

Система, яка не має жодного розвязку, називається несумісною.

2. Для простоти записів розглянемо систему третього порядку. Нехай n=3.

(3)

А=- матриця системи; Х=; В=.

AX=B.

Нехай матриця А невироджена, тобто визначник не дорівнює 0. |А|¹ 0. У (4) випадку існує обернена матриця до даної АА^-1 = А^-1А = Е.

Домножимо обидві частини матричного рівняння (4) на А^-1 зліва:

А^-1АХ = А^-1В;

ЕХ = А^-1В;

Х = А^-1В.

Наприклад:

А=; В=.

|А|=2 Þ |А|¹ 0.

А^-1= ;

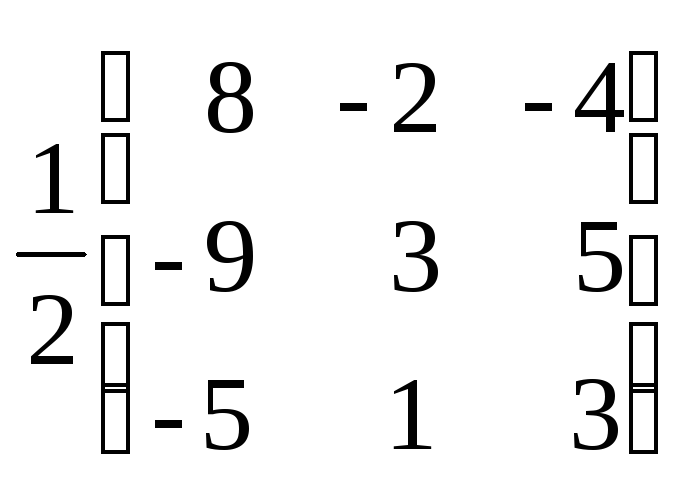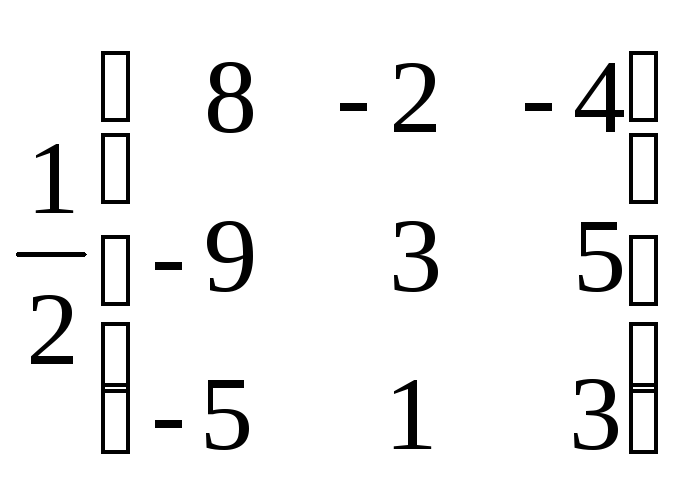
Х= ==. Таким чином х₁=1, х₂=-2, х₃=3.

3. Розглядаємо n рівнянь з n невідомими. Для простоти викладу знову візьмемо n=3, тобто розглянемо систему (3).

Позначимо D = |А|= - визначник системи.

ТЕОРЕМА: Якщо визначник системи (3) D ¹ 0 , то система (3) має розвязок (причому єдиний) і цей розв’язок знаходиться за формулами:

х₁= ; х₂=; х₃=. (Ці формули називаються формулами Крамера),

де D₁=;D₂= ;D₃= .

Наприклад, розв’яжемо систему

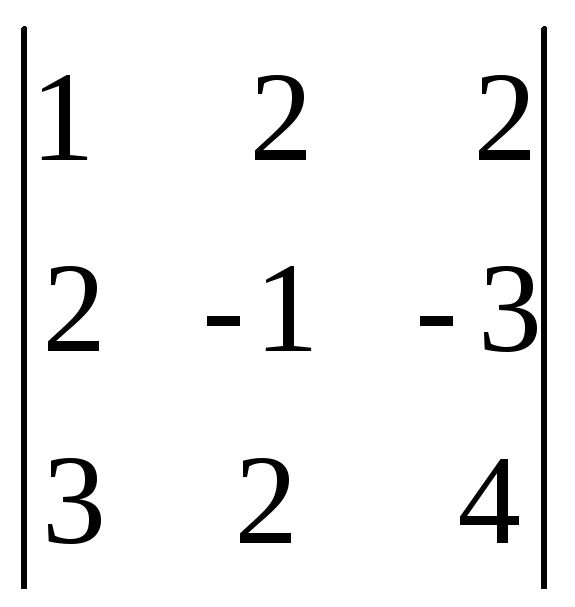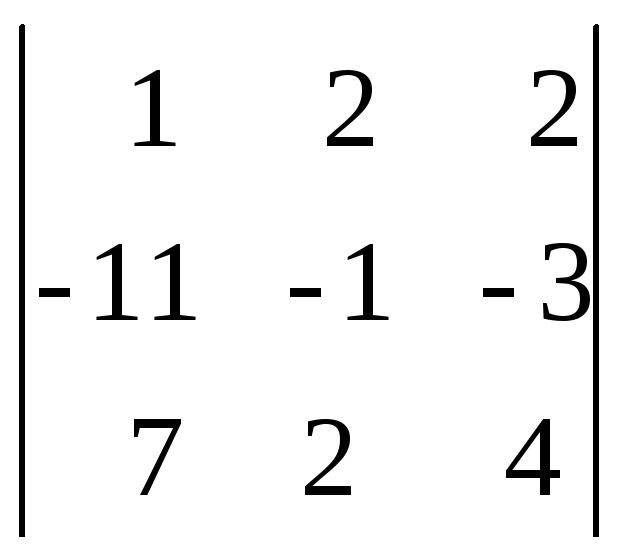D = |А|= = -18.D ¹ 0. D₁= = 18; х₁=.

D₂= 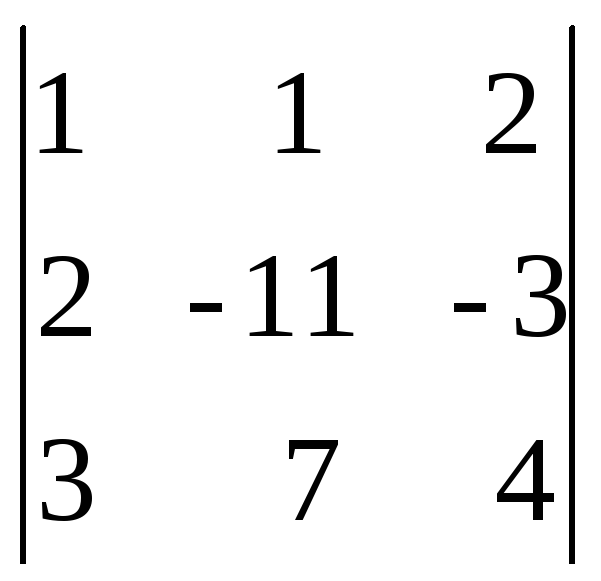=54; х₂ =. Аналогічно D₃=-72; х₃ =.

4. Нехай маємо систему вигляду

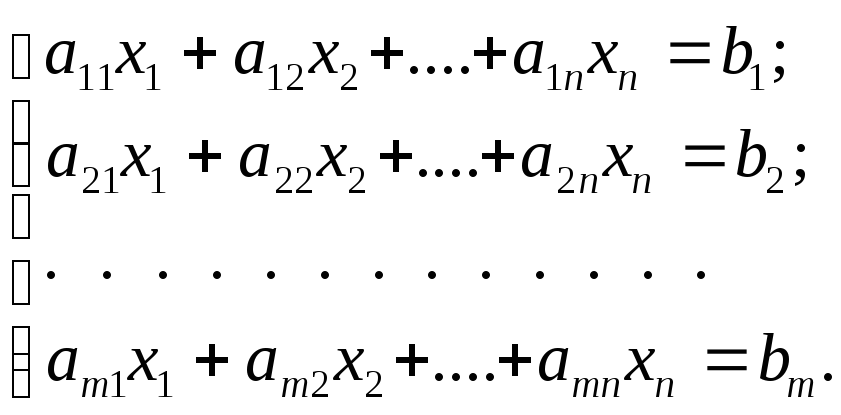
Метод Гаусса служить для розв’язування довільних систем.

Розглянемо поняття елементарного перетворення.

Елементарними перетвореннями є:

1)перестановка місцями двох рівнянь;

2)множення двох частин деякого рівняння на число, яке не дорівнює нулю;

3)додавання до обох частин деякого рівняння відповідних частин іншого рівняння, помножених на одне і те ж число.

В результаті елементарних перетворень одержимо рівносильну до неї систему.

Розглянемо перетворення системи (2).

Нехай а₁₁¹ 0. Поділимо перше рівняння на а₁₁. Перше рівняння набуде вигляду : .

Перше рівняння множимо на -а₂₁ і додаємо до другого рівняння і т. д.

Отримаємо

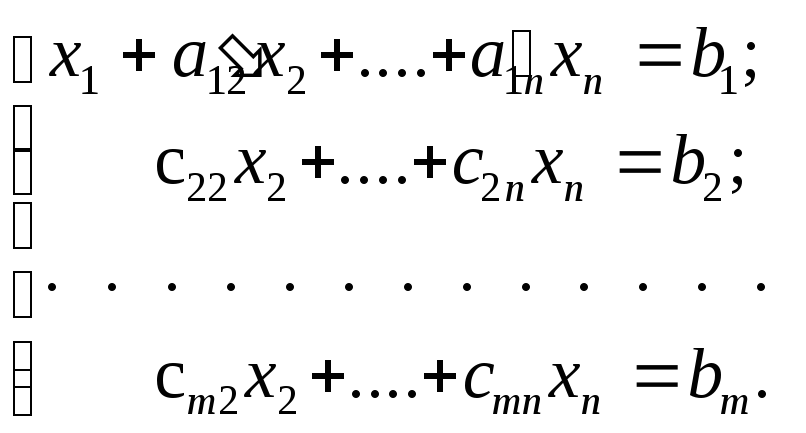
Нехай с₂₂¹0 і виконаємо дії аналогічні попереднім у всіх рівняннях, починаючи з третього рівняння виключимо х₂. Після певної кількості таких кроків одержимо систему наступного виду:

1) Одержимо несумісну систему (якесь із рівнянь в лівій частині буде мати нулі, а права не дорівнює нулю) - тоді система розв’язків немає.

2) одержимо систему у вигляді трикутника. З останнього рівняння визначаємо х_n- .Тоді послідовно всі інші х в спадному порядку. В цьому випадку система має один розвязок.

3) одержимо систему у вигляді трапеції. В цьому випадку система має безліч розвязків.