Контрольні запитання

1. Які рівняння називаються диференціальними?

2. Що називається розв’язком диференціального рівняння? Яка характерна особливість розв’язків дифрівнянь?

3. Що називається порядком диференціального рівняння?

4. Що таке інтегральна крива?

5. Що називається інтегралом дифрівняння?

6. Яке рівняння називається дифрівнянням першого порядку?

7. Який розв’язок називається загальним, частковим, особливим?

8. Сформулюйте задачу Коші.

9. Які рівняння називаються дифрівняннями з відокремлюваними змінними? Як розв’язати такі рівняння?

Тема 20. Диференціальні рівняння 1-го порядку

Мета. Розглянути деякі класи дифрівнянь 1-го порядку та методи їх розв’язання.

План.

1. Однорідні рівняння.

2. Лінійні рівняння першого порядку.

1. Функція F(x,y) називається однорідною степеня k, якщо для всіх >0 виконується рівність F(x, y)= ^kF(x, y). Прикладом однорідної функції може бути будь-яка форма (однорідний многочлен) степеняь k. Функції

,

наприклад, є однорідними відповідно степеня 0, 1, 2, k відповідно.

Диференціальне рівняння

(1)

називається однорідним, якщо f(x,y) – однорідна функція степеня нуль.

Диференціальне рівняння першого порядку в симетричній формі

є однорідним, якщо А(х,у) В(х,у) – однорідні функції одного степеня.

Однорідне рівняння можна розглядати в будь-якій однорідній (інваріантній відносно розтягу або стиску) області, наприклад, у куті з вершиною О тощо.

Заміна у=zx приводить однорідне рівняння до рівняння з відокремлюваними змінними. Однорідне рівняння можна також звести до рівняння з відокремлюваними змінними за допомогою переходу до полярних координат: х=cos, y=sin.

Рівняння виду:

можна звести до однорідного за допомогою лінійної заміни

х=х₀+t, y=y₀+z,

де х₀, у₀ – координати точки перетину прямих а₁х+b₁y+c₁=0 i a₂x+b₂y+c₂=0. Якщо ці прямі не перетинаються, то і рівняння можна звести до рівняння з відокремлюваними змінними за допомогою заміни

а₁х+b₁y+c₁=z.

Приклад 1. Розв’язати рівняння:

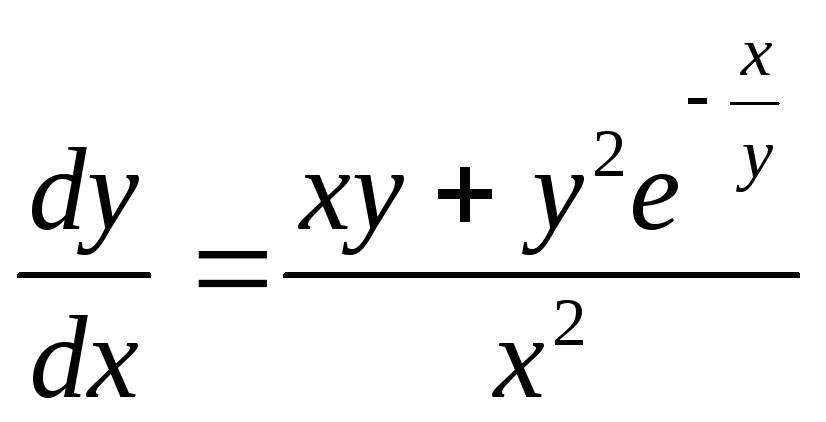
Розв’язання.

Дане рівняння однорідне. Поклавши у=zx, дістанемо

.

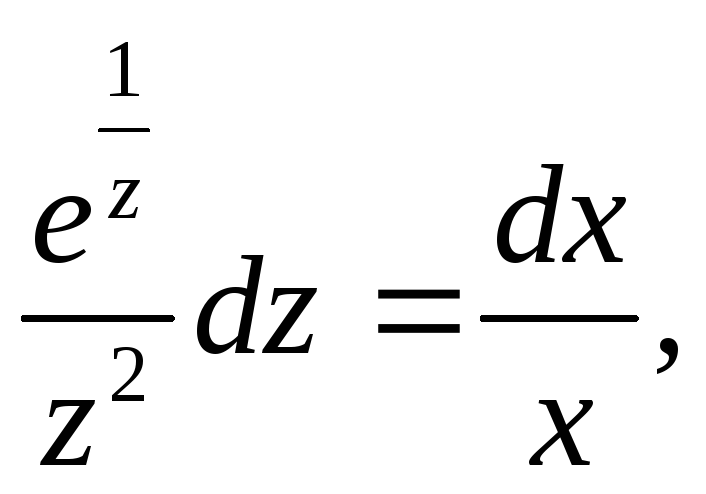
Приклад 2. Розв’язати рівняння

(

Розв’язання.

Поклавши y=xz, дістанемо

(x-xzcosz)dx+xcosz(xdz+zdx)=0

або

звідки після інтегрування

Отже,

.

2. Диференціальне рівняння

, (2)

де а(х), b(x) – довільні неперервні функції, лінійне відносно функції у=у(х).

Загальними методами розв’язування лінійних рівнянь є метод Лагранжа (варіації довільної сталої), Бернуллі та Ейлера.

Метод Лагранжа. Лінійне однорідне рівняння (відповідне (2)), яке є рівнянням з відокремлюваними змінними, розв’язується за формулою

, (3)

Маємо

, (4)

де с – довільна дійсна стала.

Розв’язок рівняння (2) знахожимо у формі (4), але при с=с(х), тобто

. (5)

Підставляючи (5) в (2), дістанемо диференціальне рівняння для знаходження функції с(х):

, (6)

звідки

. (7)

Розв’язки рівняння (3) задаються співвідношенням у=у₀+у₁. Маємо

. (8)

Розв’язок задачі Коші з початковою умовою у(х₀)=у₀ має вигляд

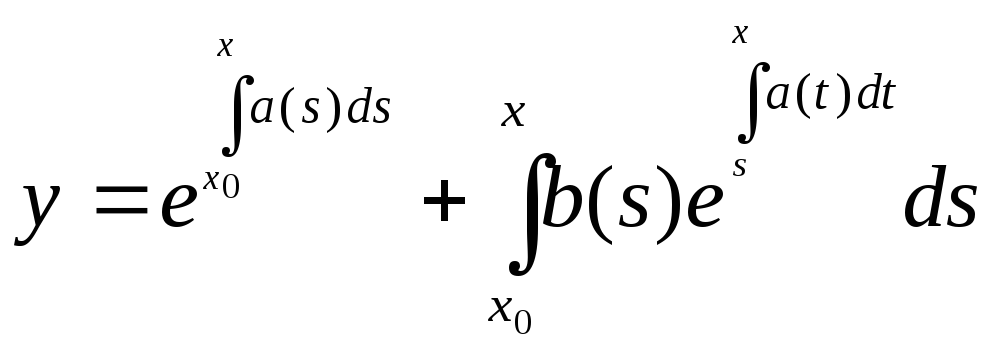. (9)

Метод Бернуллі. Розв’язки рівняння (2) шукаємо у вигляді

(10)

Маємо

u'v+uv'+a(x)uv=b(x)

uv'+v(u'+a(x)u)=b(x)

функцію u(x) виберемо з умови u'+a(x)u=0. Звідси

(11)

тоді для функції v(x):

, (12)

де С – довільна стала.

Перемноживши (11), (12) дістанемо (8).

Метод Ейлера (інтегрувального множника). Помноживши рівняння (2) на функцію - інтегруючий множник, добуте рівняння запишемо у вигляді

.

Інтегрування останнього дає

,

що еквівалентне (8).

Рівняння (8) називають формулою загального розв’язку лінійного неоднорідного рівняння (1).

Приклад 3 . Розв’язати рівняння .

Розв’язання.

Задане рівняння є лінійним відносно функції у=у(х). Продемонструємо на прикладі цього рівняння кожний із запропонованих методів.

Метод Лагранжа дає такий ланцюжок перетворень:

.

Отже, загальний розв’язок заданого рівняння має вигляд

Метод Бернуллі приводить до інших перетворень:

для маємо, звідкидлязвідки

Остаточно

Метод інтегрувального множника вимагає виконання таких перетворень: знаходимо ; помноживши рівняння на знайдену функцію, дістанемозвідки