Скориставшись цим, маємо

Теорему Ньютона- Лейбніца. Нехай функція f(x) інтегровна на відрізку [a,b] і Ф(x)- деяка первісна цієї функції на [a,b]. Тоді

.

Формула Ньютона- Лейбніца дає нам зв’язок між визначеним та невизначеним інтегралом функції.

3.Аналогічно до методів інтегрування невизначених інтегралів виділяємо три основні методи інтегрування визначених інтегралів.

Інтегрування частинами

Якщо функції u(x), v(x) та їх похідні неперервні на проміжку(a,b), то формула інтегрування частинами для визначеного інтегралу набуде вигляду

.

Інтегрування методом заміни змінної

При обчислені означеного інтеграла методом заміни змінної означений інтеграл заміниться за допомогою підстановкиu=(t) на означений інтеграл від змінної u. При цьому старі межі інтегрування слід замінити новими , , які знаходяться з вихідної підстановки: а саме, =(a), =(b).

Таким чином

.

Метод інтегрування розкладу

Переноситься на визначений інтеграл автоматично за рахунок використання властивостей визначеного інтегралу.

Контрольні запитання

1. Яка задача приводить до поняття визначеного інтегралу. Що таке Т-розбиття?

2. Що називається визначеним інтегралом?

3. Сформулюйте і доведіть властивості визначеного інтегралу.

4. Які класи функцій є інтегровними?

5. Сформулюйте теорему про середнє.

6. Сформулюйте теорему Ньютона- Лейбніца.

7. Які методи обчислення визначеного інтегралу ви знаєте?

Тема 18. Застосування визначеного інтеграла

до розв’язування задач

Мета. Навчитись розв’язувати деякі геометричні, механічні та фізичні задачі, використовуючи означений інтеграл та його властивості.

План.

1. Застосування визначеного інтегралу до розв’язування геометричних задач.

2. Застосування визначеного інтегралу до розв’язування задач фізики.

1. Площа в прямокутних координатах.

Якщо неперервна крива задана в прямокутних координатах рівнянням y=f(x) [f(x)0], то площа криволінійної трапеції, обмеженої цією кривою, двома вертикалями в точках х=а і х=b і відрізком осі абсцис ахb, визначається формулою:

(1)

Приклад.

Обчислити площу, обмежену кривою х=2-у-у² і віссю ординат.

Розв’язування.

Тут змінені ролі осей координат і тому шукана площа виразиться інтегралом:

,

де межі інтегрування у₁=-2 і у₂=1 знайдені як ординати точок перетину даної кривої з віссю ординат.

В більш загальному випадку, якщо площа S обмежена двома неперервними кривими y=f₁(x) i y=f₂(x) і двома вертикалями х=а і х=b, де f₁(x)f₂(x) при ахb, будем мати:

(2)

Якщо крива задана рівняннями в параметричній формі х=(t), у=(t), то площа криволінійної трапеції, обмеженої цією кривою, двома вертикалями, відповідними х=а і х=b, і відрізком осі ОХ, виражається інтгералом:

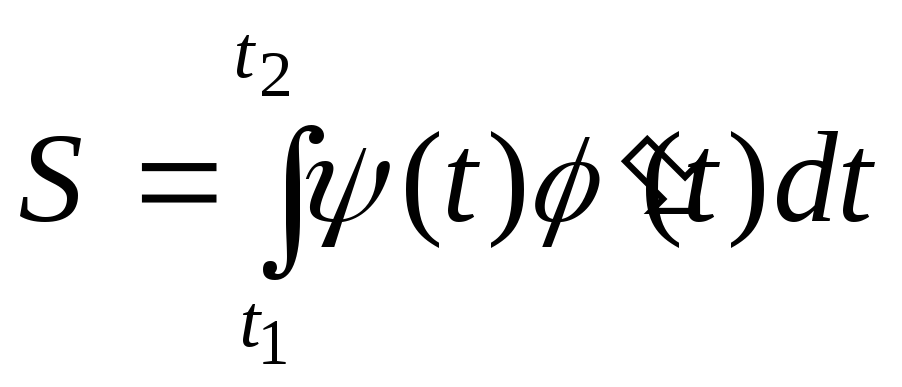, (3)

де t₁ i t₂ визначаються із рівнянь а=(t₁) і b=(t₂) ((t)0 на відрізку [t₁, t₂]).

Приклад.

Знайти площу еліпса S, використовуючи його параметричне рівняння

.

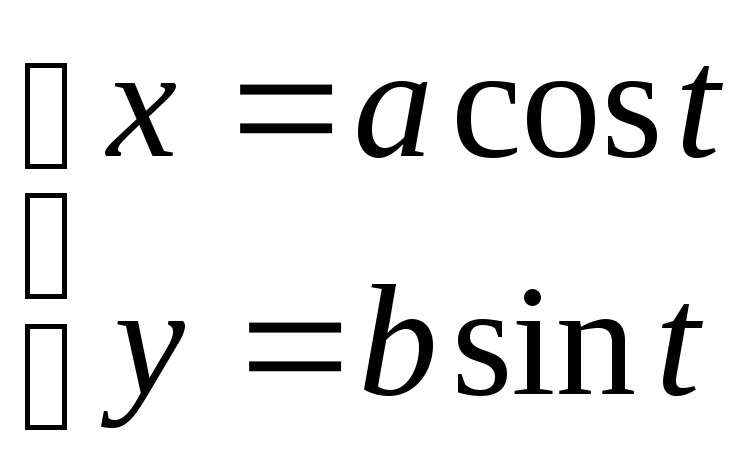Розв’язування.

Завдяки симетрії достатньо обчислити площу однієї чверті, а потім помножити її на 4. Вважаючи в рівнянні x=acost спочатку х=0, потім х=а, одержимо межі інтегрування і. Тому

,

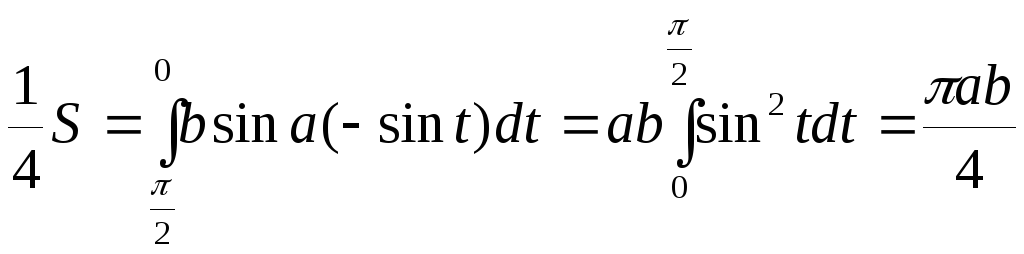і значить, S=ab.

Площа в полярних координатах.

Якщо неперервна крива задана в полярних координатах рівнянням r=f(), то площа сектора АОВ, обмеженого дугою кривої і двома полярними радіусами ОА і ОВ, які відповідають значенням ₁= і ₂=, виразиться інтегралом:

. (4)

Приклад.

Знайти площу, заключену в середину лемнискати Бернуллі r²=a²cos2.