Контрольні запитання

1. Які задачі приводять до розгляду поняття про похідну?

2. Дати означення похідної та пояснити її фізичний і геометричний зміст.

3. Яка функція називається диференційованою в точці х, на інтервалі?

4. Сформулювати і довести необхідну ознаку диференційованості функції? Що можна сказати про оберенену теорему?

5. Сформулювати і довести основні властивості диференційованих функцій.

6. Що таке логарифмічне диференціювання. Поясніть на прикладі.

Тема 12. Диференціал функції. Похідні вищих порядків

Мета. Ознайомитись з методами та способами знаходження похідних основних класів функцій.

План.

1. Диференціал першого порядку, його геометричний та механічний зміст.

2. Похідні та диференціали вищих порядків.

3. Правило Лопіталля та його застосування.

1. Означення диференційовної функції можна дати і не використовуючи поняття похідної.

Означення: Функцію f(x) назвемо диференційовною в точці х, якщо приріст цієї функції в точці х можна зобразити у вигляді:

, (1)

де і числоА не залежить від .

Попереднє означення рівносильне щойно данному. Приріст складається з двох доданків іПри фіксованомух обидва доданки є нескінченно малими функціями при прямуючому до 0. Одначе ці нескінченно малі функції мають різний порядок.є нескінченно малою функцією вищого порядку ніж, іншими словами перший доданок незмірно великий в порівнянні з другим. Це дає змогу вважати перший доданок головною частиною приросту функції. Ця головна частина є лінійною відносно.

Означення: Лінійна відносно х частина приросту диференційовної функції в точці х називається диференціалом цієї функції в цій точці і позначається Диференціал незалежної змінної х позначають dx=x. Отже, формулу диференціалу можна записати і у вигляді

Нехай функція f(x) диференційовна в точці х. Тоді в точці (x, f(x)) графік функції має дотичну, нахилену до осі абсцис під кутом , З малюнка видно АВ=МА.

Тобто, диференціал функції в точці х дорівнює приросту ординати дотичної до кривої y=f(x) в точці х, коли незалежна змінна х дістає приріст х. Відмітимо, що диференціал функції може бути і більшим, і меншим, і рівним приросту.

2. Нехай функція f(x) визначена в інтервалі (a; b). До цих пір ми користувалися поняттям похідної . Це похідна першого порядку. Якщо в інтервалі(a; b) існує похідна першого порядку і якщо ця похідна, яка є в свою чергу функцією, має похідну по x в усіх точках інтервалу , то похідна від першої похідної називається за означеннямпохідною другого порядку від цієї функції або другою похідною і позначається ,.

Похідна другого порядку, розглядувана як деяка функція, визначена в інтервалi, може мати похідну в інтервалі. Похідна від похідної другого порядку називаєтьсяпохідною третього порядку відносно даної функції або третьою похідною .

Взагалі похідна n–го порядку функції визначається як похідна похідної порядку (n-1) . Інтервал , в якому визначена похідна n -го порядку може збігатися з інтервалом , в якому визначена функція, а може бути і частиною цього інтервалу.

Наприклад

;

;

;

і т.д.

Справедливе наступне твердження:

Якщо функції f(x) і (x) мають похідні n порядку в точці x, то в цій точцi мають похідну порядку n і функції cf(x), f(x)+ (x), f(x)- (x), f(x)(x), причому

;

;

;

Правильність цих рівностей випливає з основних правил диференціювання функцій.

Функція f(x), що має похідну n-го порядку в точці x називається n разів диференційовною в цій точці. Якщо функція n разів диференційовна в кожній точці інтервалу (a,b), то вона називається n разів диференційованою в цьому інтервалі.

Якщо функція визначена на відрізку [a; b], має похідну на інтервалі (a; b), а в точці a (b) має праву (ліву) похідну , то кажемо, що функція f(x) має похідну на відрізку [a; b]. Якщо цю праву (ліву) похідну розглядати як функцію, то можна говорити про її диференційовність, а значить і про праву (ліву) похідну другого порядку в відповідних точках. Функцію назвемо двічі диференційовною, на відрізку [a; b], якщо вона двічі диференційовна на інтервалі (a; b) і має праву (ліву) похідну другого порядку в точках a і b відповідно.

Аналогічно означається похідна n порядкy на відрізку [a; b].

Нехай функція f(x) задана на інтервалі (a; b), тоді диференціал цієї функції запишемо у вигляді , деx - незалежна змінна, і, отже, dx=x.

Диференціал функції є функція, залежна від двох незалежних змінних x і x. Припустимо, що x - фіксоване стале. Тоді диференціал функції є функція від х. Якщо диференціал є функція, диференційовна в усіх точках інтервалу , то в цьому інтервалі можна говорити про диференціал від диференціала або про диференціал другого порядку, позначається .

Диференціал другого порядку, розглядуваний як деяка функція, визначена в інтервалi , може бути диференційовний в інтервалі. Диференціал від диференціала другого порядку називаєтьсядиференціалом третього порядку відносно даної функції або третім диференціалом.

Взагалі диференціал n–го порядку функції визначається як диференціал диференціала порядку (n-1) . Інтервал , в якому визначений диференціал n-го порядку може збігатися з інтервалом , в якому визначена функція, а може бути і частиною цього інтервалу.

Позначають .

Інваріантність форми для диференціалів вищих порядків порушується.

3. Нехай функції f(x) і (x) визначенні в інтервалі (a;b), скінченному чи нескінченному. Розкрити невизначеність означає знайти границю , за умови, що , і для всіх , або знайти границю , за умови, що , і для всіх .

Зауважимо, що позначення зовсім не означає, що ми ділимо на нуль, це символічне позначення факту відношення нескінченно малих функцій. Аналогічний смисл мають і позначення,тощо.

У багатьох випадках допомагає розкривати такі невизначеності правило Лопіталя.

Теорема 1. Нехай функції f(x) і (x) диференційовні в інтервалі (a;b).

Якщо: 1) ;

2) для всіх ;

3)існує границя , скінченна чи нескінченна, то

=.

Якщо: 1) ;

2) для всіх;

3) існує границя, скінченна чи нескінченна, то

=.

Теорему дано для односторонніх границь, однак вона правильна і для границь.

Наслідок. Нехай функції f(x) і (x) диференційовні в інтервалах (x₀-;x₀) i (x₀;x₀+), де >0.

Якщо: 1) ;

2) для всіх x(x₀-;x₀) i (x₀;x₀+);

3)існує границя , скінченна чи нескінченна, то

=.

Теорему та наслідок називають першим правилом Лопіталя.

Приклад. Знайти границю функції .

Розв’язання.

Тут виконані всі умови наслідку з теореми 1. За правилом Лопіталя маємо

.

Для знаходження границі виразу, що стоїть в правій частині, ще раз застосуємо правило Лопіталя:

.

Отже, =1/6.

Теорема 2. Нехай функції f(x) і (x) диференційовані в інтервалі (a;b).

Якщо: 1) ;

2) для всіх ;

3) існує границя , скінченна чи нескінченна, то

=.

Якщо: 1) ;

2) для всіх;

3) існує границя, скінченна чи нескінченна, то

=.

Теорему дано для односторонніх границь, однак вона правильна і для границь.

Наслідок. Нехай функції f(x) і (x) диференційовні в інтервалах (x₀-;x₀) i (x₀;x₀+), де >0.

Якщо: 1) ;

2) для всіх x(x₀-;x₀) i (x₀;x₀+);

3) існує границя , скінченна чи нескінченна, то

=.

Теорему та наслідок називають другим правилом Лопіталя.

Невизначеності типу розкриваємо за допомогою перетворення їх до вигляду, після чого застосовуємо перше правило Лопіталя.

Невизначеність виду розкриваємо зводячи її до вигляду за допомогою перетворення:.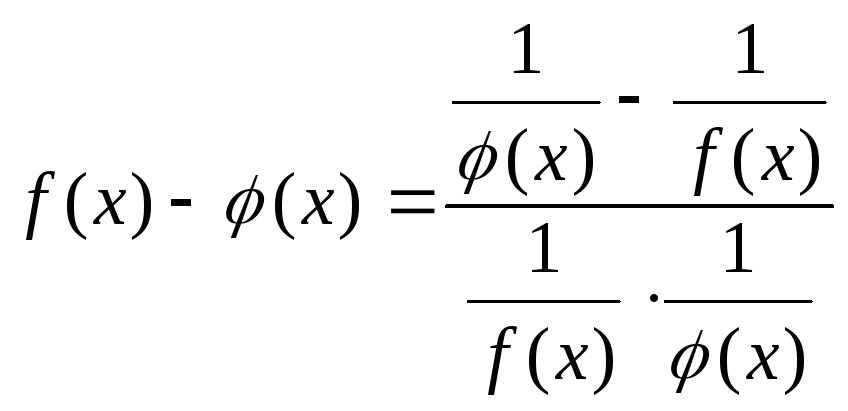

Невизначеності видів зводяться до невизначеності видуза допомогою перетворення

.