
- •Пояснювальна записка
- •Розділ 1. Матриці та вектори
- •Тема 1. Матриці та визначники. Мінори. Обернена матриця.
- •Контрольні запитання
- •Тема 2. Системи лінійних рівнянь
- •Контрольні запитання
- •Тема 3. Довільні системи лінійних рівнянь
- •Контрольні запитання
- •Тема 4. Елементи векторної алгебри
- •Контрольні запитання
- •Розділ 2. Основи аналітичної геометрії
- •Тема 5. Пряма лінія на площині
- •Контрольні запитання
- •Тема 6. Криві другого порядку
- •Контрольні запитання
- •Тема 7. Площина та її рівняння
- •Видно, що ,( тобто площина паралельна до осіOx.
- •4. Кут між двома площинами.
- •Нехай маємо площину задану нормальним рівнянням
- •Контрольні запитання
- •Тема 8. Пряма в просторі
- •Контрольні запитання
- •Розділ 3. Вступ до математичного аналізу Тема 9. Функція та її границя. Основні теореми про границю.
- •Контрольні запитання
- •Тема 10. Неперервність функції в точці
- •Контрольні запитання
- •Контрольні запитання
- •Тема 12. Диференціал функції. Похідні вищих порядків
- •Контрольні запитання
- •Тема 13. Дослідження функцій за допомогою похідної
- •Контрольні запитання
- •Розділ 5. Функції багатьох змінних
- •Тема 14. Границя функції багатьох змінних
- •Контрольні запитання
- •Тема 15. Частинні похідні та диференціали вищих порядків. Застосуваня частинних похідних
- •Контрольні запитання
- •Розділ 6. Інтегрування функції однієї змінної
- •Тема 16. Первісна функція та неозначений інтеграл
- •3. Таблиця основних інтегралів
- •Контрольні запитання
- •Тема 17. Визначений інтеграл та його обчислення
- •Скориставшись цим, маємо
- •Таким чином
- •Розв’язування. В силу симетрії кривої визначаєм спочатку одну чверть шуканої площі
- •Контрольні запитання
- •Розділ 7. Звичайні диференціальні рівняння
- •Тема 19. Поняття про диференціальні рівняння, рівняння з відокремлюваними змінними
- •Основна задача теорії інтегрування диференціальних рівнянь
- •Контрольні запитання
- •Тема 20. Диференціальні рівняння 1-го порядку
- •Диференціальне рівняння
- •Контрольні запитання
- •Тема 21. Лінійні диференціальні рівняння n-го порядку з постійними коефіцієнтами
- •Контрольні запитання
- •Перелік рекомендованої літератури
- •Тема 1. Матриці та визначники. Мінори. Обернена матриця 4с.
Контрольні запитання
Що є рівнянням лінії на площині?
Який вектор називається напрямним?
Який вектор називається нормальним?
Як задати пряму через фіксовану точку і напрямний вектор? Доведіть.
Як задати пряму через фіксовану точку і нормальний вектор? Доведіть.
Як задати пряму через дві задані точки? Доведіть.
Як задати пряму через початкову точку і кут нахилу прямої до осі абсцис? Доведіть.
Виведіть загальне рівняння прямої.
Як знайти кут між двома прямими, заданими різними способами?
Як обрахувати відстань між точкою і прямою?
Тема 6. Криві другого порядку
Мета: Дати означення кривих другого порядку та їх основних властивостей. Розглянути канонічні рівняння кривих другого порядку та зведення довільних рівнянь до канонічних.
План.
Еліпс. Зведення рівняння еліпса до канонічного вигляду. Ексцентриситет і директриса еліпса.
Гіпербола. Зведення рівняння гіперболи до канонічного вигляду.
Парабола. Зведення рівняння параболи до канонічного вигляду.
1.Еліпс- геометричне місце точок на площині, сума віддалей яких до двох заданих точок (фокусів) є величина стала і більша ніж відстань між фокусами.
MF1=MF2=2a
![]()
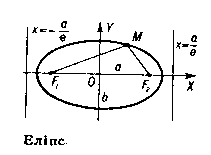 ,
2a>2c. Позначимо
,
2a>2c. Позначимо
![]() ,
,
![]() ,
,
![]() .
.
![]()
![]()
![]() +
+
![]() =2a
– рівняння
еліпса.
=2a
– рівняння
еліпса.
Проведемо ряд перетворень:
![]() =2a-
=2a-
![]() ,
,
![]() =(2a-
=(2a-
![]() )2
)2
![]() .
.
Після скорочення отримаємо
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Враховуючи,
що
![]() ,
позначимо
,
позначимо
![]() .
.
Отримаємо
![]() -
канонічне рівняння еліпса.
-
канонічне рівняння еліпса.
З наведених вище рівностей видно, що а - половина заданої сталої величини, с - половина відстанні між фокусами, а b - деяка величина, що залежить від них обох.
Дослідимо форму еліпса.
З
рівняння видно, що якщо точка
![]() належить
еліпсу, то точки
належить
еліпсу, то точки
![]() ,
,![]() ,
,![]() також
належать еліпсу. Отже, точка О(0;0) – центр
симетрії еліпса.
також
належать еліпсу. Отже, точка О(0;0) – центр
симетрії еліпса.
При
y=0
![]() тобто точки
тобто точки![]() належать
еліпсу. Аналогічно, при х=0
належать
еліпсу. Аналогічно, при х=0![]() тобто
точки
тобто
точки![]() теж належать еліпсу.
теж належать еліпсу.
Розглянемо
![]() .
Звідси видно, що при зростанні х від 0
до а y спадає від b до 0, і навпаки при
спаданні х від а до 0 y зростає від 0 до
b.
.
Звідси видно, що при зростанні х від 0
до а y спадає від b до 0, і навпаки при
спаданні х від а до 0 y зростає від 0 до
b.
2а=А1А2 – називається великою віссю еліпса (або фокальною віссю), а – велика піввісь, 2b – мала вісь, b – мала піввісь.
Розглянемо
величину
![]() ,
так як с<a, тоe<1.
З іншого боку
,
так як с<a, тоe<1.
З іншого боку
![]() ,
тобто 0<e<1.
,
тобто 0<e<1.
![]() .
Величнаe
характеризує форму еліпса. Чим ближча
вона до 0, тим більше еліпс схожий на
коло. При e=0
отримаємо коло.
.
Величнаe
характеризує форму еліпса. Чим ближча
вона до 0, тим більше еліпс схожий на
коло. При e=0
отримаємо коло.
e - називаємо ексцентриситетом еліпса.
Директриса
еліпса – це
пряма, яка проходить перпендикулярно
до фокальної осі на відстанні
![]() від центра. Тобто, існує дві директриси:х
=
від центра. Тобто, існує дві директриси:х
=
![]() і
і
х
= -![]() .
.
Побудуємо
еліпс
![]() .
.
Зведемо
рівняння до канонічного виду і знайдемо
рівняння директрис та координати
фокусів.
![]() .
.![]() .Звідси
с=±3.
.Звідси
с=±3.
Таким
чином,
![]() і
і![]()
![]() -
рівняння директрис.
-
рівняння директрис.
2. Гіпербола - сукупність точок на площині, абсолютна величина різниці віддалей яких до двох даних точок (фокусів) є величина стала. (Ця величина не дорівнює нулю і менша ніж віддаль між фокусами).
А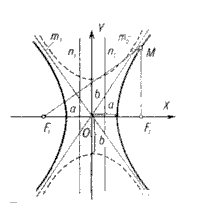 налогічно
до виведення рівняння еліпса, позначимо
відстань між фокусами
налогічно
до виведення рівняння еліпса, позначимо
відстань між фокусами![]() .
Виберемо деяку точку
.
Виберемо деяку точку
![]() .
.
Тоді
![]() .F1M
i F2M
назвемо фокальними радіусами.
.F1M
i F2M
назвемо фокальними радіусами.
Рівняння
гіперболи набере вигляду:
![]()
Провівши перетворення, аналогічні до попереднього пункту, отримаємо:
![]() -
канонічне рівняння гіперболи.
-
канонічне рівняння гіперболи.
(Проведіть доведення самостійно).
Дослідимо форму гіперболи.
гіпербола має дві осі симетрії і центр симетрії - точку початку координат.
2)
При y=0
![]() тобто точки
тобто точки![]() належать
гіперболі. Аналогічно, при х=0 -
належать
гіперболі. Аналогічно, при х=0 -![]() ®
рівняння розв’язку не має.
®
рівняння розв’язку не має.
Вісь симетрії, яка перетинає гіперболу називається дійсною віссю (це вісь Ох). 2а=А1А2 – називається дійсною віссю гіперболи , а – дійсна піввісь.
Вісь симетрії, яка не перетинає гіперболу називається уявною віссю (це вісь Оy), 2b – уявна вісь, b – уявна піввісь.
Розглянемо
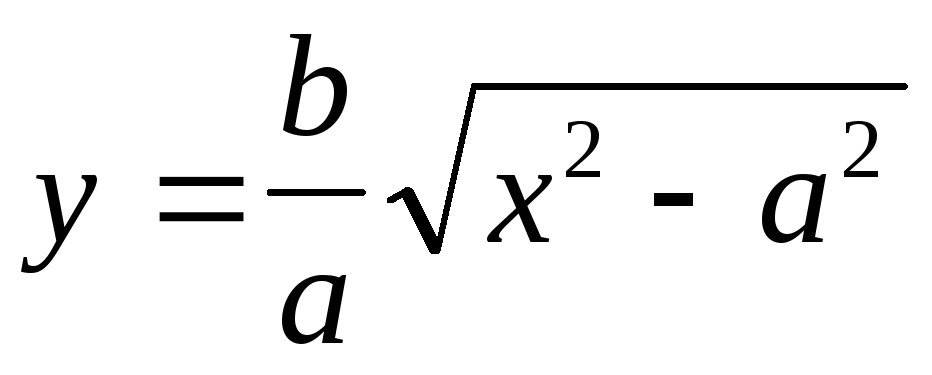 .
Звідси видно, що при зростанні х зростає
y.
.
Звідси видно, що при зростанні х зростає
y.Розглянемо пряму
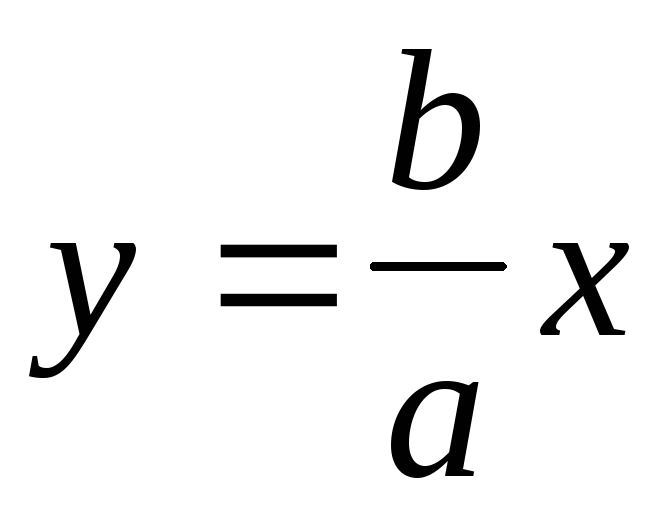 і деяку точку N(x; y), що належить гіперболі.
Знайдемо відстань від прямої до точки.
Обчислимо відстань від точки М, що
лежить на прямій до точки N, коли вони
мають однакові абсциси.
і деяку точку N(x; y), що належить гіперболі.
Знайдемо відстань від прямої до точки.
Обчислимо відстань від точки М, що
лежить на прямій до точки N, коли вони
мають однакові абсциси.
![]() .
.
Якщо х®¥, то MN®0. Але відстань між точкою і прямою менша за знайдену нами MN, тому MP®0 також.
За
означенням пряма
![]() -
асимптота гіперболи. Враховуючи симетрію
гіперболи маємо
-
асимптота гіперболи. Враховуючи симетрію
гіперболи маємо![]() - також асимптота гіперболи.
- також асимптота гіперболи.
Гіперболи виду
![]() і
і
![]() називаються спряженими.
називаються спряженими.
Якщо a=b, то гіпербола називається рівнобічною.
Аналогічно
до поняття ексцинтриситету еліпса,
вводимо поняття ексцинтриситету
гіперболи.
![]() ,e>1.
Велична e
характеризує форму гіперболи.
,e>1.
Велична e
характеризує форму гіперболи.
e - називаємо ексцентриситетом гіперболи.
Д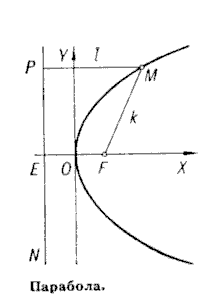 иректриса
гіперболи
– це пряма, яка проходить перпендикулярно
до дійсної осі на відстанні
иректриса
гіперболи
– це пряма, яка проходить перпендикулярно
до дійсної осі на відстанні
![]() від центра. Тобто, існує дві директриси:
х =
від центра. Тобто, існує дві директриси:
х =![]() і х=-
і х=-![]() .
.
3. Парабола - геометричне місце точок, рівновіддалених від заданої точки (фокуса) та заданої прямої (директриси).
Нехай
задано точку F
і пряму p.
Точка М(x, y)
буде належати параболі, якщо MР=MF,
де N-
основа перпендикуляра опущеного з точки
М
на пряму. Нехай
![]() ,
а рівняння директриси
,
а рівняння директриси![]() .
Тоді
.
Тоді![]() .
Це рівняння є рівнянням параболи.
Проведемо ряд перетворень:
.
Це рівняння є рівнянням параболи.
Проведемо ряд перетворень:
![]()
![]()
![]() -
канонічне рівняння параболи.
-
канонічне рівняння параболи.
Дослідимо форму параболи:
парабола має вісь симетрії Ox.
при y=0 маємо x=0, тобто точка О(0; 0) належить параболі і її називають вершиною параболи.
Так як в лівій частині рівності завжди число невід’ємне, то
 ,
тобто крива розміщена в додатній
півплощині відносно x.
,
тобто крива розміщена в додатній
півплощині відносно x. .
При зростанні x
абсолютна величина y
зростає.
.
При зростанні x
абсолютна величина y
зростає.
