Контрольні запитання

1. Які функції називаються однорідними?

2. Які дифрівняння називаються однорідними? Як їх розв’язують?

3. Які рівняння називають лінійними? Наведіть приклад.

4. Як розв’язують лінійні дифрівняння?

5. Які рівняння називають рівняннями Бернулі та Ріккаті? Наведіть приклади. Як їх розв’язують?

Тема 21. Лінійні диференціальні рівняння n-го порядку з постійними коефіцієнтами

Мета. Розглянути дифрівняння з сталими коефіцієнтами та дослідити їх розв’язки.

План.

1. Інтегрування лінійних однорідних диференціальних рівнянь зі сталими коефіцієнтами.

2. Інтегрування лінійних неоднорідних диференціальних рівнянь зі сталими коефіцієнтами.

1. Лінійним однорідним диференціальним рівнянням n-го порядку зі сталими коефіцієнтами називається рівняння виду

, (1)

де . Многочленстепеняn виду

(2)

називається характеристичним многочленом лінійного диференціального оператора зі сталими коефіцієнтами . Рівняння

(3)

називається характеристичним рівнянням оператора .

Розглянемо деякі випадки, які можуть виникнути після розв”язання рівняння (3).

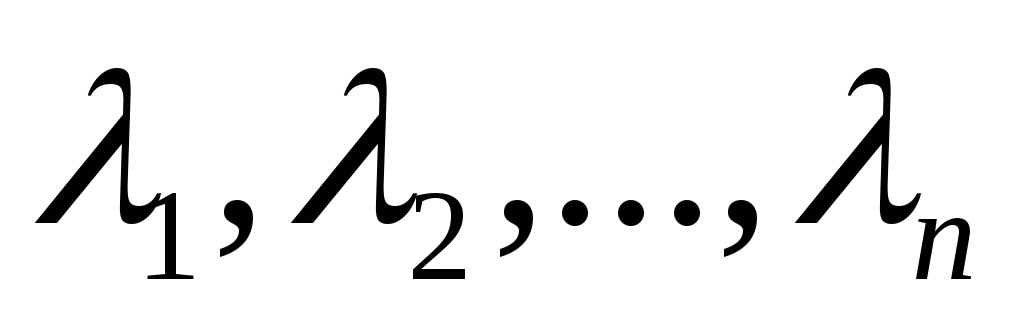1. Якщо - корені рівняння (3), причому вони всі є дійсними числами і різні між собою (тобто не існує однакових коренів). Тоді функції

утворюють фундаментальну систему розв”язків рівняння (1). Загальний розв”язок рівняння (1) матиме вигляд

,

де - деякі дійсні сталі.

2. Якщо - корені рівняння (3) з деякою кратністю відповідно,,причому вони всі є дійсними числами. Тоді функції

,

,….,

.

утворюють фундаментальну систему розв”язків рівняння (1). Загальний розв”язок рівняння (1) матиме вигляд лінійної комбінації вказаних функцій і n довільних дійсних сталих.

Якщо в рівнянні (1) коефіцієнти - дійсні числа, а характеристичне рівняння (3) має дійсні корені:k₁–кратності m₁, k₂-кратності m₂, k_r-кратності m_r, а також комплексні корені, які входять комплексно-спряженими парами з однаковою кратністю:кратності-кратностікратності то фундаментальну систему розв’язків рівняння (1) можна вибрати в дійсній формі

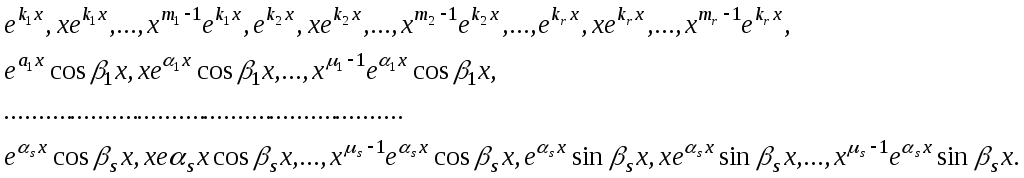
Отже, лінійні однорідні рівняння зі сталими коефіцієнтами завжди можна проінтегрувати в елементарних функціях, причому інтегрування зводиться до алгебраїчних операцій.

Приклад 1. Знайти загальні розв’язки рівнянь:

а) б)

Розв’язання.

а) Знаходимо корені характеристичного рівняння МаємозвідкиФундаментальну систему розв’яків утворюють функції,,.

б) Знаходимо корені характеристичного рівняння МаємозвідкиФундаментальну систему розв’язків утворюють функції,,.

Отже,

а)

б)

довільні сталі.

Приклад 2. Знайти загальний розв’язок рівняння

Розв’язання.

Знаходимо корені характеристичного рівняння

Маємо:

Звідси

2. Лінійними неоднорідними диференціальними рівняннями n-го порядку зі сталими коефіцієнтами називається рівняння виду

(1) де неперервна нафункція,,

Оскільки фундаментальну систему розв’язків відповідного однорідного рівняння завжди можна побудувати, то задача інтегрування рівняння (1) зводиться до задачі побудови якого-небудь частинного розв’язку рівняння (1). Частинний розв’язок рівняння (1) завджи можна знайти, застосовуючи метод варіації довільних сталих (Лагранжа) або метод Коші.

а) якщо права частина в (1) має спеціальний вид

де - комплексна (зокрема дійсна) стала, яка називається контрольним числом функції;- многочлен степеня, то знаходження частинного розв’язку по суті зводиться до алгебраїчних операцій. Нехай контрольне числоє коренем характеристичного рівняння операторакратності(якщо, то дістанемо резонансний випадок; якщоне є коренем характеристичного рівняння, тоі дістанемо нерезонансний випадок). Тоді рівняння (1) має єдиний частинний розв’язок виду

де - многочлен степеня, коефіцієнти якого можна знайти за допомогою методу невизначених коефіцієнтів.

б) Якщо коефіцієнти рівняння (1) – дійсні числа, а права частина має спеціальний вид

де - дійсні сталі,- многочлени степеняівідповідно з дійсними коефіцєнтами, то рівняння (1) має єдиний частинний розв’язок виду

де -- кратність контрольного числафункціїяк кореня характеристичного рівняння оператора(- резонансний випадок,-нерезонансний випадок),- многочлени степеня, коефіцієнти яких можуть бути знайдені методом невизначених коефіцієнтів.

Отже, лінійні неоднорідні рівняння зі сталими коефіцієнтами завжди можна проінтегрувати в квадратурах, причому у випадку, коли права частина рівняння (1) - функція має спеціальний вид (2) або (4), інтегрування по суті зводиться до алгебраїчних операцій.

Приклад 1. Знайти загальний розв’язок рівняння

Розв’язання.

Характеристичне рівняння має розв’язкиі. Загальний розв’язок відповідного однорідного рівнянняПрава частина даного рівнянняЗвідси,так які. Диференціюючидва рази і підставляючи похідні в дане рівняння, дістанемо:

Скоротивши на і порівнявши коефіцієнти при перших степеняхх і вільні члени в лівій і правій частині рівності, дістанемо 5А=4 і 7А+5В=0, звідки і

.

Приклад 2. Знайти загальний розв’язок рівняння

Розв’язання.

Характеристичне рівняння має двохкратний корінь. Права частина рівняння має виглядтуті. Частковий розв’язок оскільки співпадає з двократним коренемі, тому,

Диференціюючи два рази, підставляючи в рівняння і прирівнюючи коефіцієнти, дістаємоЗвідси, загальний розв’язок даного рівняння записується у вигляді

Приклад 3. Знайти загальний розв’язок рівняння

Розв’язання. Характеристичне рівняння має розв’язкиі. Загальний розв’язок відповідного однорідного рівняння буде[см. 3), де ]:

Права частина вигляду

де Їй відповідає частковий розв’язок

(тут N=1, a=0, b=1, r=1).

Диференціюючи два рази і підставляючи в рівняння, порівнюємо коефіцієнти в обох частинах рівності при cosx, xcosx, sinx, xsinx. В результаті дістаємо чотири рівняння з яких і визначаються,. Тому

Загальний розв’язок