Контрольні запитання

1. Що називається функцією з кількома змінними?

2. Що називається областю визначення, областю значень, аргументами?

3. Що таке лінія, поверхня рівня?

4. Що називається границею функції кількох змінних?

5. Яка функція називається неперервною в точці , на області?

6. Що називається частинною похідною?

7. Що називається частинним диференціалом функції кількох змінних?

8. Що називається повним диференціалом функції кількох змінних?

9. Яка достатня умова неперервності функції?

10. Наведіть приклад застосування повного диференціала до наближених обчислень.

Тема 15. Частинні похідні та диференціали вищих порядків. Застосуваня частинних похідних

Мета. Оволодіти апаратом частинних похідних для розв’язування деяких прикладних задач.

План.

1. Частинні похідні та диференціали вищих порядків.

2. Поняття про екстремум функції 2-ох незалежних змінних.

3. Умовний екстремум. Найбільше і найменше значення функції.

1.Частинні похідні функції від кількох змінних є в свою чергу функціями від тих самих змінних, тому від них також можна визначити частинні похідні. Таким чином ми отримуємо частинні похідні 2-го порядку. Диференціювання таких частинних похідних 2-го порядку приведе в свою чергу до частинних похідних 3-го порядку і т.д.

У випадку функції змінних z=f(x;y) отримаємо:

• частинні похідні 1-го порядку:

(1)

• частинні похідні 2-го порядку:

; (2)

.

Для таких похідних використовуються також позначення:

(3)

Друга і четверта похідні в (2) і (3) називаються мішаними.

Без доведння приймемо теорему 1:

Якщо частинні похідні вищого порядку неперервні, то мішані похідні одного і того ж порядку, що відрізняються тільки порядком диференціювання, рівні між собою.

Приклад. Обчислити часинні похідні до 3-го порядку включно для функції

U=x⁴+x²y²+y⁵+1.

Розв’язування.

(Порівняйте 2-гу і 3-тю формули).

Диференціалом другого порядку від функції z=f(x;y) називають диференціал від її повного диференціалу

d²z=d(dz). (4)

Аналогічно:

d³z=d(d²z);

dⁿz=d(d^n-1z).

Якщо x,y -незалежні змінні і функція має неперервні частинні похідні, то справедливі формули:

і взагалі, має місце символічна формула:

(5)

яка розкривається по біномінальному закону.

Якщо ж x i y- функції від однієї чи декількох незалежних змінних, то повний диференціал другого порядку шукається з застосуванням (4)

. (6)

Приклад. Знайти повні диференціали 1-го і 2-го порядків для

z=4x²-6xy+5y².Розв’язування.

,

.

Далі

,

2.Означення. Функція z=f(x;y) має максимум (мінімум) в точці М(x₀;y₀), якщо в її околі (f(x;y)<f(x₀;y₀)).

Це означення поширюється і на функції більшої кількості змінних.

Максимуми і мінімуми функції називаються екстремумами, а точки в яких вони досягаються – точками екстремуму.

Зрозуміло, що якщо у функції f зафіксувати всі змінні, крім однієї, то отримаємо функцію однієї змінної, яка буде мати екстремум там же, що й функція кількох змінних. Звідси слідує, що в цій точці значення відповідної частинної похідної або дорівнює 0, або не існує.

Для знаходження екстремумів:

1. Знаходимо критичні точки, тобто ті в яких частинні похідні 1-го порядку рівні нулеві: (якщо всі частинні похідні = 0, то така точка є стаціонарною) або не існують.

2. Визначаємо величини:

.

3. Складаємо детермінант =АС-В².

4. Якщо >0, то функція має в М₀ – екстремум. А саме: якщо А>0 (чи С>0) – мінімум; якщо А<0 (чи C>0) – мінімум; якщо А<0 (чи C<0) – максимум.

Якщо <0, то в точці М₀ екстремуму немає.

Якщо =0, то проблема потребує додаткових досліджень.

Приклад. Знайти екстремум функції

z=x²+xy+y²-3x-6y

Розв’язування.

1. 

2. Знаходим стаціонарні точки: 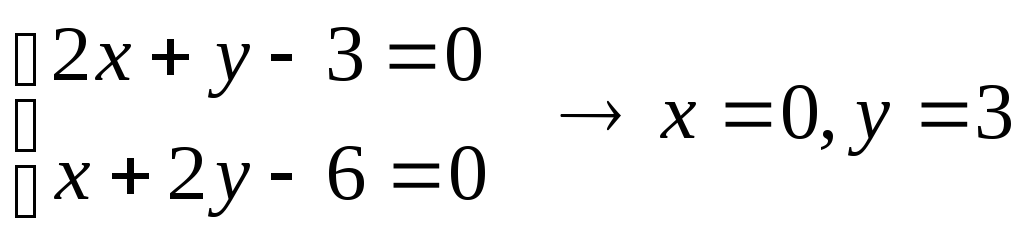М(0;3)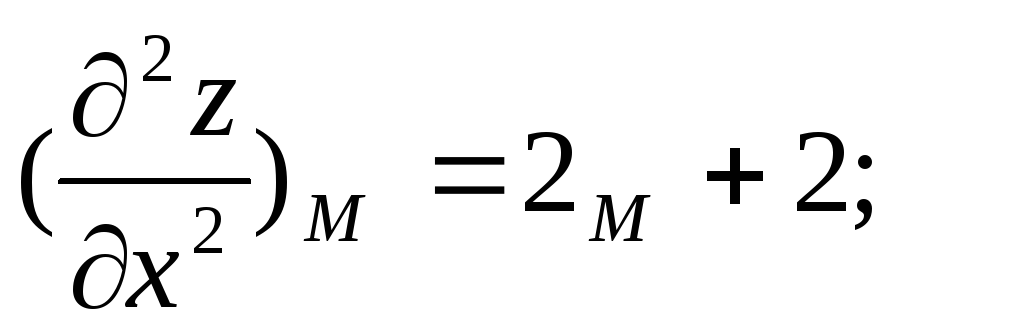

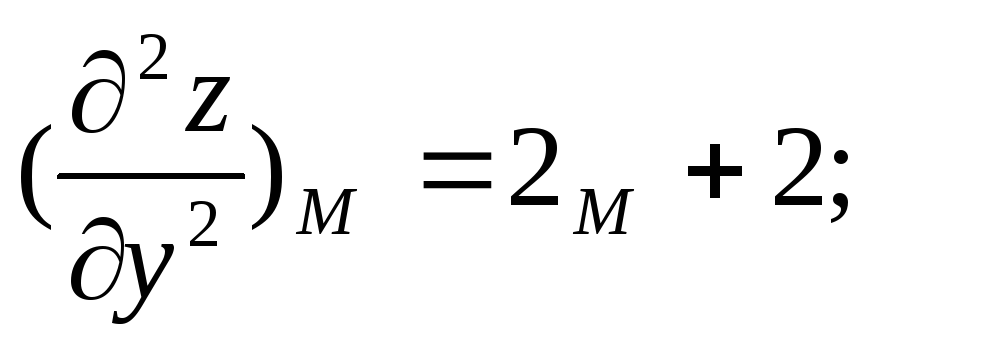
3. 

4. =2^.2-1=3>0; A>0

в т. М₀(0;3) z=x²+xy+y²-3x-6y має мінімум.

Z_min=0²+0^.3+3^.0-6^.3=9-18=-9.

3. Означення. Умовним екстремумом функції z=f(x;y) називається екстремум цієї функції, досягнутий за умови, що х i y зв‘язані рівнянням зв’язку (х,у)=0.

Його знаходження зведемо до дослідження на звичайний екстремум функції Лагранжа , де-невизначений множник.

Тоді маємо систему

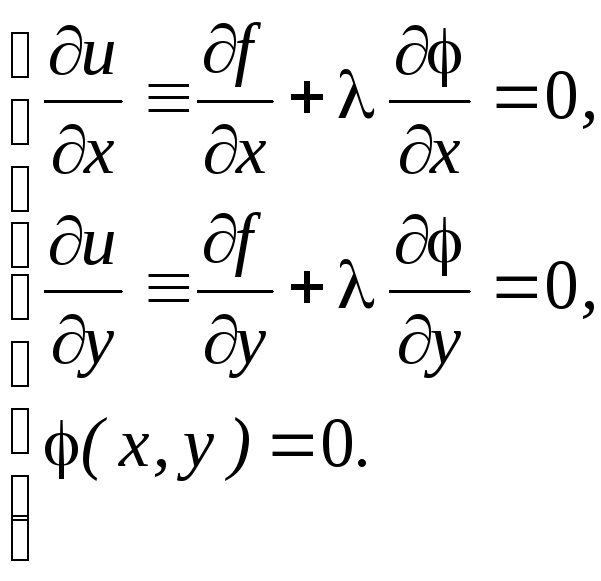
Звідси знайдемо х, у, .

Для знаходження найбільшого і найменшого значення в замкнутій області потрібно:

1. Знайти стаціонарні точки в цій області і обчислити значення функцій в цих точках;

2. Знайти найбільше і найменше значення на границі області;

3. З всіх значень вибрати найбільше і найменше.

Приклад. Знайти екстремуми z=xy, якщо х і у зв’язані рівнянням

2х+3у-5=0.

Розв’язування.

u=xy+(2x+3y-5)

.
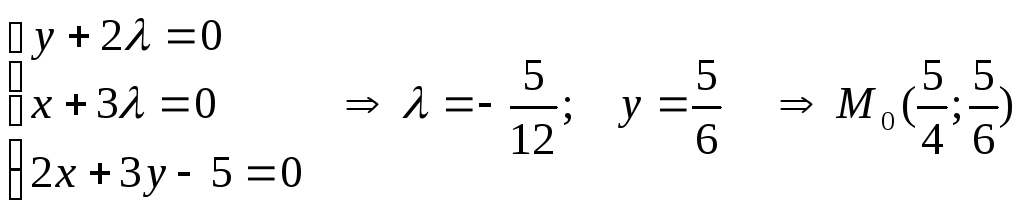