
- •Пояснювальна записка
- •Розділ 1. Матриці та вектори
- •Тема 1. Матриці та визначники. Мінори. Обернена матриця.
- •Контрольні запитання
- •Тема 2. Системи лінійних рівнянь
- •Контрольні запитання
- •Тема 3. Довільні системи лінійних рівнянь
- •Контрольні запитання
- •Тема 4. Елементи векторної алгебри
- •Контрольні запитання
- •Розділ 2. Основи аналітичної геометрії
- •Тема 5. Пряма лінія на площині
- •Контрольні запитання
- •Тема 6. Криві другого порядку
- •Контрольні запитання
- •Тема 7. Площина та її рівняння
- •Видно, що ,( тобто площина паралельна до осіOx.
- •4. Кут між двома площинами.
- •Нехай маємо площину задану нормальним рівнянням
- •Контрольні запитання
- •Тема 8. Пряма в просторі
- •Контрольні запитання
- •Розділ 3. Вступ до математичного аналізу Тема 9. Функція та її границя. Основні теореми про границю.
- •Контрольні запитання
- •Тема 10. Неперервність функції в точці
- •Контрольні запитання
- •Контрольні запитання
- •Тема 12. Диференціал функції. Похідні вищих порядків
- •Контрольні запитання
- •Тема 13. Дослідження функцій за допомогою похідної
- •Контрольні запитання
- •Розділ 5. Функції багатьох змінних
- •Тема 14. Границя функції багатьох змінних
- •Контрольні запитання
- •Тема 15. Частинні похідні та диференціали вищих порядків. Застосуваня частинних похідних
- •Контрольні запитання
- •Розділ 6. Інтегрування функції однієї змінної
- •Тема 16. Первісна функція та неозначений інтеграл
- •3. Таблиця основних інтегралів
- •Контрольні запитання
- •Тема 17. Визначений інтеграл та його обчислення
- •Скориставшись цим, маємо
- •Таким чином
- •Розв’язування. В силу симетрії кривої визначаєм спочатку одну чверть шуканої площі
- •Контрольні запитання
- •Розділ 7. Звичайні диференціальні рівняння
- •Тема 19. Поняття про диференціальні рівняння, рівняння з відокремлюваними змінними
- •Основна задача теорії інтегрування диференціальних рівнянь
- •Контрольні запитання
- •Тема 20. Диференціальні рівняння 1-го порядку
- •Диференціальне рівняння
- •Контрольні запитання
- •Тема 21. Лінійні диференціальні рівняння n-го порядку з постійними коефіцієнтами
- •Контрольні запитання
- •Перелік рекомендованої літератури
- •Тема 1. Матриці та визначники. Мінори. Обернена матриця 4с.
Основна задача теорії інтегрування диференціальних рівнянь
Як було сказано вище, процес знаходження розв’язку даного диференціального рівняння називається інтегруванням цього рівняння. Якщо при цьому вдається виразити весь розв’язок в елементарних функціях, то кажуть, що рівняння проінтегроване в елементарних функціях. Саме з таким рівнянням ми мали справу в задачі 1.
Якщо рівняння не інтегрується в елементарних функціях, але всі його розв’язки виражаються через невизначені інтеграли від елементарних функцій, то кажуть, що рівняння проінтегровано в квадратурах. Квадратурою називається операція взяття невизначеного інтегралу. Наприклад, всі розв’язки рівняння
![]()
даються формулою
![]()
2. Диференціальним рівнянням першого порядку називається співвідношення виду
![]() ,
(6)
,
(6)
де
х
– незалежна змінні (аргумент); у=у(х)
– невідома функція аргументу х;
![]() -задана
функція змінних
-задана
функція змінних
![]() Рівняння (1) не розв’язане
відносно похідної.
Рівняння (1) не розв’язане
відносно похідної.
Рівняння виду
![]() ,
(7)
,
(7)
де f(x,y) – задана функція двох змінних, називається диференціальним рівнянням першого порядку, розв’язаним відносно похідної.
Часто використовують симетричну форму запису диференціального рівняння першого порядку:
![]() ,
,
де P(x,y), Q(x,y) – задані функції змінних х і у.
Розв’язком
диференціального рівняння (6) або (7) на
інтервалі І
називається неперервно диференційовна
функція
![]() ,
яка перетворює це рівняння в тотожність
наІ,
тобто
,
яка перетворює це рівняння в тотожність
наІ,
тобто
![]()
![]() ,
,
![]()
Співвідношення
Ф(х,у)=0
називається інтегралом
рівняння (4) або (5),
якщо воно неявно задає розв’язок
![]() цього
рівняння.
цього
рівняння.
Графік
розв’язку
![]() називаєтьсяінтегральною
кривою диференціального рівняння.
Проекція інтегральної кривої на вісь
ординат називається фазовою
кривою або траєкторією диференціального
рівняння.
називаєтьсяінтегральною
кривою диференціального рівняння.
Проекція інтегральної кривої на вісь
ординат називається фазовою
кривою або траєкторією диференціального
рівняння.
Через кожну точку (х;у) області визначення рівняння (7), проведемо пряму, тангенс кута нахилу якої до осі абсцис дорівнює f(x,y). Ця сім’я прямих називається полем напрямків рівняння (7) або полем напрямків функції f(x,y).
Інтегральна крива в кожній своїй точці дотикається до поля напрямків функції f(x,y). Крива, яка в кожній своїй точці дотикається до напрямку, що є в цій точці, є інтегральною кривою.
Ізокліною називається крива, в кожній точці якої напрямок поля однаковий. Усі інтегральні криві, які перетинають дану ізокліну, утворюють з віссю абсцис один і той самий кут.
У багатьох задачах, які приводяться до диференціальних рівнянь першого порядку, потрібно знайти розв’язок, приймаючи задане значення функції при заданому значенні незалежної змінної. Така задача називається початковою задачею чи задачею Коші.
В загальному вигляді для рівняння першого порядку в нормальній формі (7) задача Коші ставиться так: вимагається знайти розв’язок
у=у(х)
рівняння яке задовільняє початкову умову (умову Коші)
у=у0 при х=х0
яке можна записати у вигляді одного співвідношення:
![]() чи
чи

При цьому вважаєм, що права частина рівняння (7) визначена при х=х0, у=у0.
Бажаючи вказати в розв’язку задачі Коші (7) початкові дані х0, у0, записують цей розв’язок у вигляді
у=у(х, х0, у0) (8)
Геометрично мова йде про знаходження інтегральної кривої, яка проходить через задану точку М0(х0,у0)
Винятково велике значення для теорії диференціальних рівнянь і її додатків має питання про існування розв’язку задачі Коші і про єдинність цього розв’язку. Будем казати, що задача Коші
![]() у=у0
при х=х0
у=у0
при х=х0
має єдиний розв’язок, якщо можна вказати такий окіл точки х0
![]() (9)
(9)
в якому визначено розв’язок (8) і не існує розв’язку у=у1(х, х0, у0), визначеного в тому же околі (9), значення якого не співпадають зі значеннями розв’язку (8) хоча б в одній точці околу (9), відмінній від точки х0. В протилежному випадку кажуть, що єдиність розв’язку задачі Коші порушена.
Коли
дано рівняння
![]() і
поставлено початкову умовуу=у0
при х=х0,
то, перш ніж знаходити розв’язок,
який задовільняє цю умову, бажано
відповісти на питання, чи існує шуканий
розв’язок,
і якщо так, то чи буде цей розв’язок
єдиним. Це особливо важливо в тих
випадках, коли розв’язок
задачі Коші шукається наближеними
методами.
і
поставлено початкову умовуу=у0
при х=х0,
то, перш ніж знаходити розв’язок,
який задовільняє цю умову, бажано
відповісти на питання, чи існує шуканий
розв’язок,
і якщо так, то чи буде цей розв’язок
єдиним. Це особливо важливо в тих
випадках, коли розв’язок
задачі Коші шукається наближеними
методами.
Розглянем рівняння першого порядку в нормальній формі
![]() (10)
(10)
Нехай D є деяка область на площині (х,у), через кожну точку якої проходить одна і тільки одна інтегральна крива рівняння (5). Наприклад, можем вважати, що в околі кожної точки області D виконується умова теореми Пікара. Функція
![]()
![]() (11)
(11)
визначена в деякій області зміни змінної х і С і неперервно диференційовна відносно х, називається загальним рівнянням в області D, якщо вона задовільняє дві умови:
рівнісь (10) має розв’язки в області D відносно довільної постійної:
![]()
2) функція (11) є розв’язком рівняння (10) при всіх значеннях довільної постійної С, задовільняючих формулу, коли точка (х,у) пробігає область D.
Знання загального розв’язку дає можливість розв’язати задачу Коші з будь-якими початковими даними х0, у0 із області D за рахунок вибору відповідного значення довільної постійної С. Для цього достатньо замінити у формулі загального розв’язку змінні х і у числами х0 і у0, розв’язавши одержане рівняння
![]()
відносно С і підставити знайдене значення С=С0 в загальний розв’язок . Одержана функція
![]()
і дасть шуканий розв’язок, при чому інших розв’язків немає.
Якщо у формулі загального розв’язку роль довільної постійної С відіграє початкове значення у0 шуканої функції у при деякому фіксованому значенні х0 незалежної змінної х
у=у(х, х0, у0),
то такий запис загального розв’язку будем називати загальним розв’язком у формі Коші.
Розв’язок, який утворюється підстановкою містить у формулу загального розв’язку конкретного (допустимого) числового значення довільної постійної (включаючи ), є частковим розв’язком.
Розв’язок у=у(х), в кожній точці якого порушується єдиність розв’язку задачі Коші, називається особливим розв’язком. Особливий розв’язок не може бути одержаний із формули загального розв’язку при конкретному числовому значенні довільної постійної С (але може бути одержаний при С=С(х)).
3. Рівняння виду
![]() (12)
(12)
називається рівнянням з відокремлюваними змінними.
Якщо g(c0)=0, то функція y=c0 є розв’язком рівняння (12). Розв’язки рівняння (12), вздовж яких g(y)0, задовольняють співвідношення
![]() ,
,
![]()
Теорема:
Нехай функції f(x)
i g(y)
визначені і неперервно диференційовні
в околах точок х=х0,
у=у0
відповідно, причому g(y0)
0.
Тоді розв’язок
![]() рівняння
(10) з початковою умовою(х0)=у0
існує в деякому околі точки х=х0,
єдиний і задавольняє співвідношення
рівняння
(10) з початковою умовою(х0)=у0
існує в деякому околі точки х=х0,
єдиний і задавольняє співвідношення
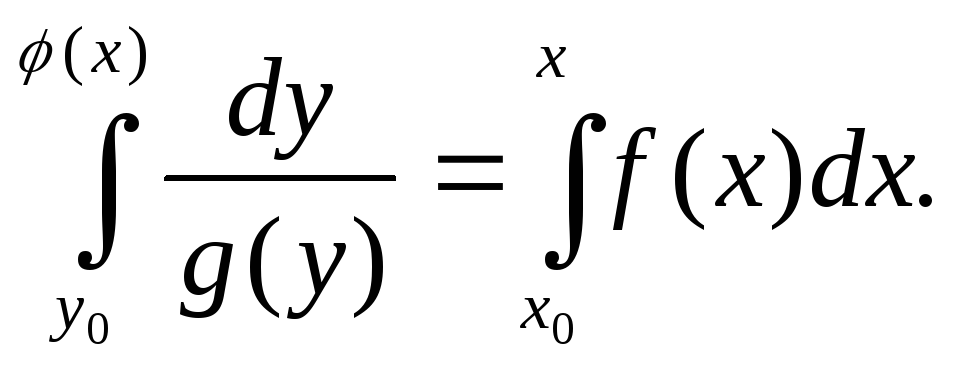
Рівняння
виду
![]() заміноюz=ax+by+c
зводиться до рівнянь з відокремлюваними
змінними.
заміноюz=ax+by+c
зводиться до рівнянь з відокремлюваними
змінними.
Приклад 3. Розв’язати рівняння
х(1+у2)+у(1+х2)у/=0.
Розв’язання.
Запишемо дане рівняння у вигляді
x(1+y2)dx+y(1+x2)dy=0.
Розділивши обидві частини цього рівняння на добуток (1+х2)(1+у2) 0, дістанемо рівняння з відокремленими змінними
![]()
Інтегруючи це рівняння, послідовно знаходимо
![]()
![]()
![]()
Звідси (1+х2)(1+у2)=С.
