
- •3) Однородное дифференциальное уравнение I порядка
- •3) Линейное дифференциальное уравнение I порядка (ур-ия Бернулли)
- •Геометрический смысл производной и дифференциала
- •2) Образовательные цели урока
- •3) Приемы создания мотивации учебной деятельности.
- •4) Тестовые задания для текущего контроля усвоения понятия и способы проверки результатов контроля.
- •2) Выберите правильный ответ:
- •3) Решите задачу
- •5) Фрагмент урока на этапе усвоения понятия
- •Свойства счётных множеств:
- •Основные свойства неопределённого интеграла
- •Свойства определённого интеграла
- •1) Вычисление площади плоских фигур.
- •2) Вычисление объёмов тел вращения.
- •3) Вычисление дуги кривой линии.
- •II. Аксиомы умножения:
- •III. Аксиомы дистрибутивности
- •Простейшие свойства групп, колец, полей
- •Гомоморфизмы групп, колец, полей
- •Свойства гомоморфизмов
- •60. Если : u V и : V w – два гомоморфизма групп или колец, то их композиция ○ : u w будет гомоморфизмом групп или колец.
- •70. Если : V w – изоморфизм групп или колец, то обратное отображение –1 : w V также является изоморфизмом групп или колец. Понятие и идея изоморфизма в современной математике
- •Внеклассное мероприятие по математике в 8 классе: «Эта забавная математика»
- •Теорема о поле комплексных чисел
- •Геометрическая интерпретация действий
- •Определение и простейшие свойства векторных пространств. Примеры
- •Подпространство, критерий подпространства, система образующих, базис и размерность векторного пространства. Примеры
- •1) Любое ненулевое конечномерное векторное пространство обладает базисом,
- •2) Любые два базиса конечномерного векторного пространства состоят из одинакового числа векторов.
- •Изоморфизм векторных пространств
- •Примерный план ответа
- •Кольцо матриц Mm n(f) и векторное пространство матриц Mm n(f)
- •Матричные уравнения
- •1.Решите систему уравнений:
- •Билет № 15. Билет №15. Многочлены от одной переменной. Делимость многочлена на двучлен Кольцо f[X] многочленов над полем
- •Деление с остатком в кольце f[X]
- •Рациональные корни многочлена с целыми коэффициентами
- •Освобождение от алгебраической иррациональности в знаменателе дроби
- •Отношение делимости в кольце z и его свойства
- •I. Организационный момент.
- •II. Устный счет.
- •III. Сообщение темы урока
- •IV. Изучение нового материала
- •V. Физкультминутка
- •Алгоритм Евклида
- •Нок целых чисел и его вычисление
- •Вычисление нод и нок целых чисел с помощью канонического разложения
- •Простые и составные числа
- •20. Если произведение нескольких сомножителей делится на p, то, по крайней мере, один из сомножителей делится на p.
- •30. Различные простые числа взаимно просты.
- •50. Если натуральное число n не делится ни на одно простое число p , тоn – простое, в противном случае оно будет составным.
- •II. Урок изучения нового материала.
- •Теоремы Эйлера и Ферма
- •Признаки делимости
- •Учебные задачи для текущего контроля
- •28.Векторное построение геометрии
- •1 Уровень.
- •2 Уровень.
- •3 Уровень.
1) Любое ненулевое конечномерное векторное пространство обладает базисом,
2) Любые два базиса конечномерного векторного пространства состоят из одинакового числа векторов.
Определение 3.5. Число векторов в любом базисе ненулевого конечномерного векторного пространства V называется его размерностью и обозначается через dim V.
Замечание 4. По определению, считают размерность нулевого векторного пространства равной 0.
Примеры: 1. Векторное пространство геометрических векторов V2 двухмерно (dim V2 = 2). Его базисы – это любые системы из двух неколлинеарных вектора.
2. Векторное пространство геометрических векторов V3 трёхмерно (dimV3 = 3). Его базисы – это любые системы трёх некомпланарных векторов.
3. Арифметическое векторное пространство Rn является n-мерным. Его стандартным базисом служит система векторов ei = (0, … , 0, 1, 0, … , 0), где 1 i n. (dim R n = n).
4. Векторное пространство решений однородной системы линейных уравнений А Х = 0 , где А Mm n(F) имеет размерность n – rg(A). Его базисом будет любая фундаментальная система решений.
Теорема 3.4. Любой вектор b V единственным образом разлагается по базису (1) (e1, e2, …, en) конечномерного векторного пространства V, то есть представляется в виде b = 1 e1 + 2 e2 + … + n en.
Определение 3.6. Пусть b= 1 e1 + 2 e2 + … + n en – разложение вектора b по базису (1) векторного пространства V над полем F. Упорядоченный набор чисел (1, 2, …, n) из поля F называется координатами вектора b в базисе (1).
Пример. В пространстве R3 система векторов e1 = (1, 0, 0), e2= (0, 2, 0), e3 = (0, 0, 3) базисом. Вектор а = (2, 4, 9) имеет координаты (2, 2, 3) в этом базисе, так как
b = 2 e1 + 2 e2 + 3 e3.
Изоморфизм векторных пространств
Определение 3.7.
Биективное
отображение
![]() :U
:U
![]() V
называется изоморфизмом
векторных пространств
U
и V
над одним и тем же полем F,
если:
V
называется изоморфизмом
векторных пространств
U
и V
над одним и тем же полем F,
если:
1)
![]() а,
b
а,
b![]() V
V
![]() (а
+ b)
=
(а
+ b)
=
![]() (a)
+
(a)
+
![]() (b);
2)
(b);
2)
![]() а
а![]() V
V
![]()
![]() F,
F,
![]() (
(![]() а)
=
а)
=
![]() (
(![]() (a))
(a))
Теорема 3.5. Два
конечномерных векторных пространства
U
и V
над одним и тем же полем F
изоморфны тогда и только тогда, когда
их размерности совпадают, то есть:
U
![]() V
V
![]() dimU
= dimV.
dimU
= dimV.
Пример.
1. V2
![]() R2,
так как dim
V2
= dim
R2
= 2, аналогично: V3
R2,
так как dim
V2
= dim
R2
= 2, аналогично: V3
![]() R3.
R3.
2.
M22(R)
![]() R4,
так как dim
M22(R)
= dim
R4
= 4.
R4,
так как dim
M22(R)
= dim
R4
= 4.
МЕТОДИКА 13.СМ 21
Билет № 14. Алгебра матриц
Примерный план ответа
Сформулировать определения операций над матрицами, привести примеры, сформулировать свойства, доказать теоремы о векторном пространстве матриц одинаковой размерности и кольце квадратных матриц n-го порядка над полем P, обосновать один из способов вычисления обратной матрицы и матричный способ решения системы линейных уравнений.
Кольцо матриц Mm n(f) и векторное пространство матриц Mm n(f)
Определение 4.1.
Пусть F
– некоторое поле, m,
n
N.
Прямоугольная таблица вида
 ,
где aij
F
(1
i
m,
1
j
n),
называется
прямоугольной
(m
n)
- матрицей
над полем F
с элементами aij
и
обозначают короче || aij
|| или буквами
А,
В,
С,
...
,
где aij
F
(1
i
m,
1
j
n),
называется
прямоугольной
(m
n)
- матрицей
над полем F
с элементами aij
и
обозначают короче || aij
|| или буквами
А,
В,
С,
...
Любая строка этой матрицы есть n-мерный арифметический вектор, а любой столбец – m-мерный арифметический вектор.
Множество всех (m n)-матриц над полем F будет обозначаться через Mm n(F). В случае m = n матрица называется квадратной порядка n.
Определение 4.2. Две матрицы A, B Mm n(F) называются равными (пишут А = В), если aij = bij (1 i m, 1 j n).
Другими словами, две матрицы равны тогда и только тогда, когда они имеют одинаковые размерности и равные соответствующие элементы.
На некоторых подмножествах множества Mm n(F) можно определить две бинарные операции (+ , ·) и две унарные операции (умножение на скаляр и нахождение обратной матрицы).
Определение 4.3. Суммой матриц A = || aij ||, B = || bij || Mm n(F) называется матрица С = A+B = || aij || + || bij ||= || aij+bi j || Mm n(F) (1 i m, 1 j n).
Определение 4.4. Произведением матрицы A = || aij || Mmn(F) на скаляр F называется матрица A= || aij || Mm n(F) (1 i m, 1 j n).
Определение 4.5. Произведение матриц A = || ais || Mmk (F) и B = || bsj ||, B Mk n(F) – это матрица С = A B = || cij ||= || ai1 · b1j+ ai2 · b2j + … + aik · akj ||, С Mmn(F) (1 i m, 1 j n, 1 s k ).
Замечание. Сложение матриц и умножения матриц на скаляры являются алгебраическими операциями на Mmn(F) – множестве матриц одинаковой размерности m × n, а умножение матриц является алгебраической операцией только на множестве Mnn(F) квадратных матриц порядка n.
Теорема 4.1 (о кольце и векторном пространстве матриц).
1) Алгебра (Mnn(F) +, ) является кольцом с единицей. Это кольцо при n > 1 некоммутативно и содержит делители нуля.
2)
Алгебра (Mnn(F),
+, {w![]() |
|![]()
![]() F})
является
векторным пространством над полем F
размерности m
n.
F})
является
векторным пространством над полем F
размерности m
n.
Замечания: 1.Роль единицы в кольце Mnn(F) играет единичная матрица (у нее на главной диагонали стоят единицы, а все другие элементы равны 0):
Еn =
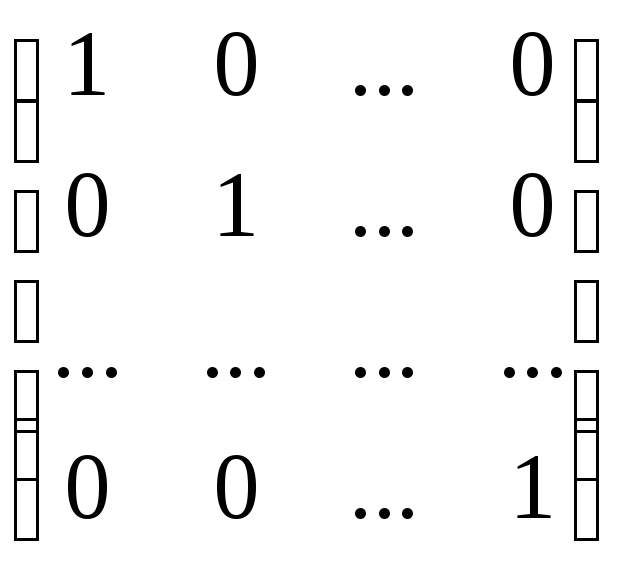
![]() Mnn(F)
Mnn(F)
2. Приведем пример делителей нуля в кольце M22(R): если
А
=
![]() ,В
=
,В
=
![]() ,
тоА
· В =
,
тоА
· В =![]()
Пример.
Вычислим: А
∙ В =
 ∙
∙ .
.
Воспользуемся правилом умножения матриц:
А
∙ В =

 =
=
 ,
где
,
где
![]() ,
при i
,
при i
![]() {1, 2, 3}, j
{1, 2, 3}, j
![]() {1, 2, 3}. Получим:
{1, 2, 3}. Получим:
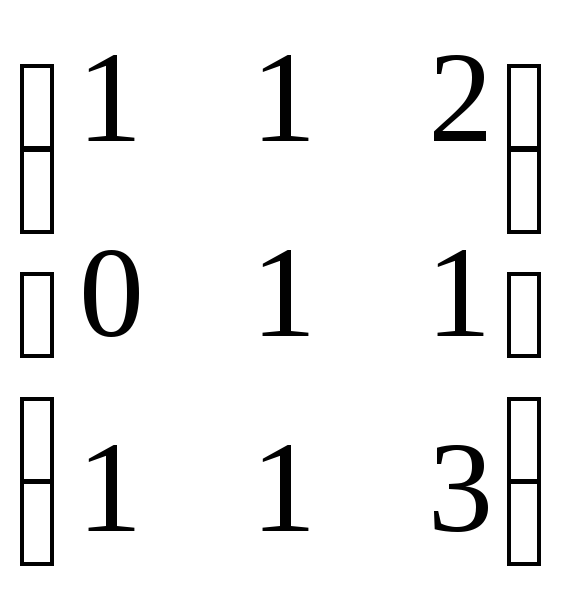 ∙
∙ =
=
 =
= .
.
Обратимые матрицы. Вычисление обратной матрицы
Определение 4.6. Матрица A Mnn(F) называется обратимой, если X Mnn(F) A X = X A = En.
Матрица X называется обратной матрицей к А и обозначается A–1.
Определение 4.7. Квадратная матрица А Mnn(F) называется неособенной (невырожденной), если ее ранг равен порядку n этой матрицы.
Замечание. Квадратная матрица А Mnn(F) является неособенной (невырожденной) тогда и только тогда, когда |A| 0.
Теорема 4. 2 (критерий обратимости матрицы). Квадратная матрица А Mnn(F) обратима тогда и только тогда, когда она неособенная.
Теорема 4. 3 (о нахождении обратной матрицы).
1) Пусть А – неособенная матрица, А Mnn(F). Рассмотрим расширенную матрицу В = (A | Еn), которая получается из А приписыванием справа матрицы Еn. Если к матрице В применить элементарные преобразования строк так, чтобы слева от черты получилась матрица Еn, то справа от черты получится матрица А-1.
(A | Еn) ~ …~ … (Еn | A–1)
2)
Пусть
A
Mnn(F).
Если
|A|
0,
то A–1
=
![]()
|| Aij||
t,
где Aij
– алгебраическое дополнение к элементу
aij
матрицы А (1
i
n,
1
j
n).
|| Aij||
t,
где Aij
– алгебраическое дополнение к элементу
aij
матрицы А (1
i
n,
1
j
n).
Пример. Вычислим обратную матрицу А-1 двумя способами:
А
= =
rang
A
=3, значит, матрица A
обратима.
=
rang
A
=3, значит, матрица A
обратима.
Вычислим А-1.
1.
Метод элементарных преобразований:
 ~
~
 ~
~
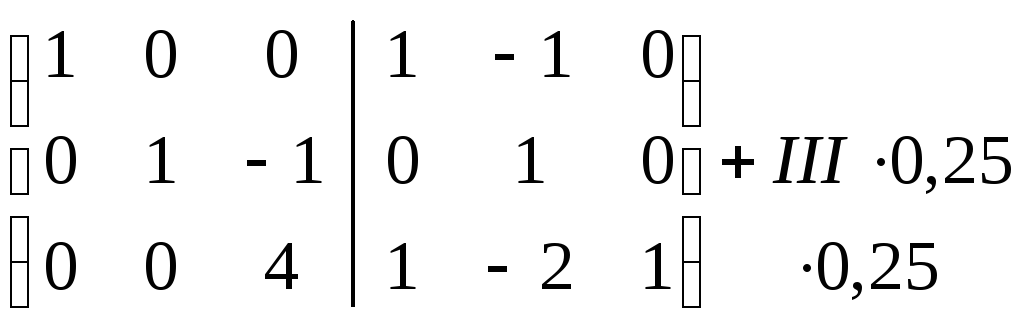 ~
~
 .Таким
образом,
.Таким
образом,
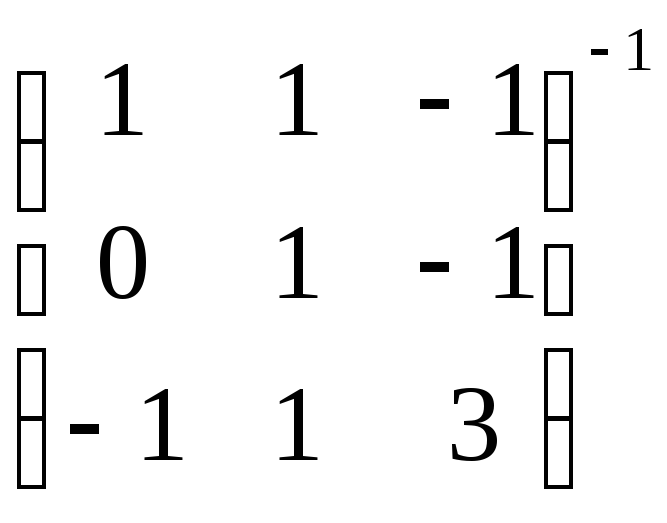 =
=
 .
.
2.
С помощью алгебраических дополнений:
A–1
=
![]()
|| Aij
|| t
(1
i
n,
1
j
n).
|| Aij
|| t
(1
i
n,
1
j
n).
|A|
=
 =
(3 + 1 + 0) –
(1 – 1 + 0)
= 4
=
(3 + 1 + 0) –
(1 – 1 + 0)
= 4
![]() 0. Поэтому А-1
обратима.
0. Поэтому А-1
обратима.
Вычисляем алгебраические дополнения элементов данной матрицы, не забывая о их знаках:
A11
= (-1)1+1·![]() =4,
A12
= (-1)1+2
·
=4,
A12
= (-1)1+2
·![]() =1,
A13
= (-1)1+3
·
=1,
A13
= (-1)1+3
·![]() =1,
=1,
A21
= (-1)2+1
·![]() =–
4,
A22
= (-1)2+2
·
=–
4,
A22
= (-1)2+2
·![]() =2,
A23
= (-1)2+3
·
=2,
A23
= (-1)2+3
·![]() =–2,
=–2,
A31
= (-1)3+1
·![]() =0,
A32
= (-1)3+2
·
=0,
A32
= (-1)3+2
·![]() =1,
A33
= (-1)3+3
·
=1,
A33
= (-1)3+3
·![]() =1.
=1.
А-1
=
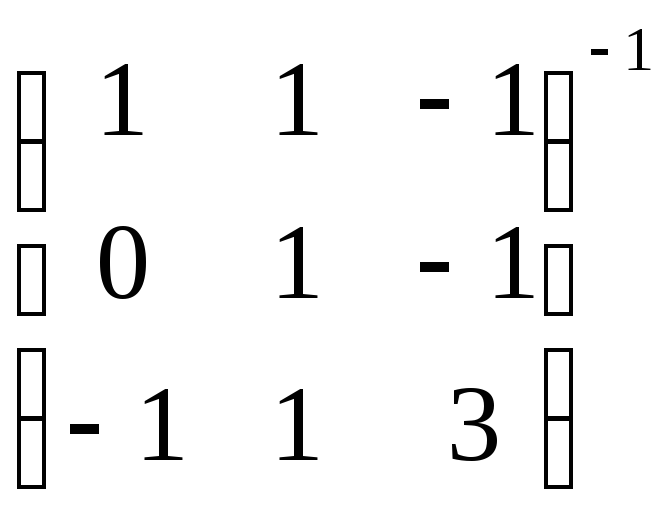 =
=![]()
 =
=![]()
 =
= .
.
Проверка:
А · А-1
=
 ·
·
 =
=
 .
.
Ответ:
А-1
=
 .
.
