Учебные задачи для текущего контроля

На формирование знания изученного материала.

1 уровень.

1.Для данных векторов иназовите:

а) сумму векторов

б) разность векторов

в)скалярное произведение векторов.

2.Продолжите предложение: равные векторы одинаково направлены и….

3. Верно ли что:

2 уровень.

1 .Вставьте пропущенное слово в определение : два нулевых вектора называются если

они лежат на одной прямой или на параллельных прямых.

2. Сформулируйте «правило параллелограмма» сложения векторов.

3 уровень.

1 .Выполните логический анализ теоремы о скалярном произведении векторов по схеме: условие, заключение, какая теорема (простая или сложная).

2. Вывести следствие из определения скалярного произведения векторов.

3. Найти данный материал по теме.

На формирование понимания изученного материала.

1уровень.

1.Привести примеры двух коллинеарных векторов.

2.Найдите ошибку по чертежу.

2 уровень.

1.Сформировать утверждение обратное к данному и доказать его:Если векторы перпендикулярны, то их скалярное произведение равно нулю. 2.Докажите, что от любой точки можно отложить вектор, равный данному вектору, и только один.

3 уровень.

1 .Привести доказательство теоремы о сумме векторов по рисунку:

2.Векторы иперпендикулярны. Докажите , что

3.Составить задачу на применение теоремы о скалярном произведении векторов.

На формирование умений и навыков.

1 уровень.

1. Даны векторы (1,-4) и(-4,8). Найдите вектор, равный сумме векторови, иабсолютную величину вектора .

2.АВСД-параллелограмм, О - точка пересечения диагоналей АС и ВД. Найдите.

2 уровень.

1 .Дан параллелограмм АВСД, , . Выразите векторы ичерези.

2.PE- медиана треугольника МРК. Найдите.

З.По данным составить условие к задаче и решить ее:

Дано: (4.-3),= 15 Найти:

3 уровень.

1 .Даны стороны треугольника – а, b ,c. Найти его медианы.

2.Докажите, что для векторов имеет место неравенство

З.Даны векторы (1,0),(1,1),(1,0). Найдите числои, чтобы имело место векторное равенство

На развитие внимания:

1 уровень.

1. .Перечислите все термины , изученные в данной теме. 2.Продолжите предложение: равные векторы имеют .... 3. Как определяется угол между векторами?

2. уровень.

1. Сформулируйте « правило параллелограмма» сложения векторов

2.Найдите ошибку в определении: два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на пересекающихся прямых.

3уровень.

В параллелограмме АВСД АВ =,АД =. Выразите векторычерез и .

На развитие восприятия.

1уровень.

1.записать с помощью символики

а)сумму и разность векторов

б)произведение вектора на число

в) скалярное произведение 2.Решить задачу

А(-3,2), В(-1,1). Найдите

2уровень.

1 .Посмотреть заданное время на лист с опорным конспектом и как можно точнее воспроизвести его.

2. Решить задачу: Дано: (4,-1)

(-2,-5)Найти:

3уровень.

Дан ненулевой вектор. Можно ли утверждать, что?

Методы и приемы проверки знаний и умений учащихся по теме

Проверка может осуществляться как в письменной (контрольная работа, самостоятельная работа, математический диктант и другие), так и в устной (зачет, опрос и другие) форме.

Задания для текущего контроля и способов быстрой проверки и оценки его результатов

Вариант №1	Вариант №2
Сформулируйте следующие определения
Что такое вектор? Что такое длина вектора? Какие векторы называются коллинеарным?	Какой вектор называется нулевым? Какие векторы называются равными? Какие векторы называются сонаправленными?
Даны векторы: .
Укажите пары коллинеарных векторов.	Укажите пары противоположно направленных векторов.
Вычислите скалярное произведение векторов и , если

Билет № 22. Прямая на плоскости.

Пусть на плоскости задана некоторая аффинная система координат и прямая l.

I. Каноническое уравнение прямой. Выберем произвольную точкуM₀(x₀ ; y₀ )  lи зафиксируем направляющий вектор a(, ) этой прямой. Тогда справедливы следующие эквивалентности:X(x; y)  l  (x–x₀ ; y–y₀) || a(; )  =   = 0 . Итак, координаты точек, расположенных на прямой l, и только они удовлетворяют следующим эквивалентным друг другуканоническим уравнениям прямой:

=

II. Параметрическое уравнение прямой. Из теории определителей известно, что   t  R   t  R .Таким образом, получаемпараметрическое уравнение прямой:

, t  R

III. Общее уравнение прямой. Преобразуем каноническое уравнение прямой:  (x–x₀)–(y–y₀ ) = 0  x+(–)y+(–x₀+y₀) = 0  Ax+By+C = 0, гдеA = , B = –, C = –x₀+y₀ иA²+B²  0, т.к. координаты,  направляющего вектора одновременно не обращаются в ноль.

Пусть теперь задано уравнение Ax+By+C = 0, гдеA²+B²  0. Докажем, что множествоL = {M(x; y)   | Ax+By+C = 0 } является прямой на плоскости. Действительно, выберем в множествеL произвольную точкуM₀(x₀ ; y₀ ): это всегда можно сделать, т.к. коэффициентыA, Bне равны одновременно нулю (например, еслиB  0, тоx₀ можно выбрать произвольно, аy₀ = –x₀–). Таким образом,Ax₀+By₀+C = 0, т.е.С = –Ax₀–By₀ . Если теперь положить = –B,  = Aи рассмотреть вектора(; ), тоа  0 т.к.²+² = = A²+B²  0и можно через т.M₀(x₀ ; y₀) провести прямуюl с направляющим векторома. Ввиду предыдущих эквивалентностей (с учётомA = , B = –, C = –x₀+y₀ иA²+B²  0) получаемAx+By+C = 0  – каноническое уравнение прямойl.

Итак, любая прямая l может быть задана с помощью уравнения Ax+By+C = 0 (A²+B²  0), которое называется общим уравнением прямой на плоскости. Обратно, каждое общее уравнение Ax+By+C = 0 (A²+B²  0) задаёт на плоскости некоторую прямую с направляющим вектором а(–B; A).

Теорема (об общем уравнении прямой на плоскости).(1) Каждая прямая на плоскости задаётся некоторым общим уравнением вида Ax+By+C = 0 (A²+B²  0).

(2) Каждое общее уравнение Ax+By+C = 0 (A²+B²  0) однозначно определяет некоторую прямую на плоскости.

(3) Два общих уравнения A₁x+B₁y+C₁ = 0, A₂x+B₂y+C₂ = 0 (A₁²+B₁²  0  A₂²+B₂²), задают одну и ту же прямую на плоскости тогда и только тогда, когда коэффициенты этих уравнений пропорциональны: = = =  R \ {0}.

(4) При аффинной замене координат общее уравнение прямой преобразуется снова в общее уравнение прямой, т.е. вид общего уравнения прямой инвариантен при аффинных преобразованиях координат.

IV. Уравнение прямой в отрезках.Полученное уравнение += 1называетсяуравнением прямой в отрезках. Смысл названия раскроется, если выяснить геометрический смысл величинa, b : эта прямая пересекает осьx в точке(a; 0), а осьy – в точке(0; b). Таким образом,величины a и b определяют отрезки, отсекаемые прямой на координатных осях (см. рис).

V. Нормальное уравнение прямой.Любую прямую можно задать уравнениемAx+By+C = 0, гдеA²+B² = 1, которое называютнормальным уравнением прямой. Смысл этого названия можно понять, если ввести следующее определение: вектор единичной длины, перепендикулярный к заданной прямой, называетсявектором нормали для этой прямой.

VI. Уравнение прямой с угловым коэффициентом.Пусть, по-прежнему, система координат декартова, и на плоскости дана прямаяAx+By+C = 0,(A²+B²  0), не параллельная оси ординат, т.е.a(–B; A) e₂(0; 1)   или B  0. Тогда Ax+By+C = 0   y = kx+b, где k = , b = . Уравнение видаy = kx+b называетсяуравнением прямой с угловым коэффициентом k.

Выясним геометрический смысл углового коэффициента k. Ясно, что прямая, параллельная оси абсцисс, имеет уравнениеy = b и угловой коэффициентk = 0.

В случае k  0 можно в­зять любые две различные точки на прямой:M₀(x₀ ; kx₀+b) и M₁(x₁; kx₁+b). Тогда векторa = (x₁–x₀ ; k(x₁–x₀)) будет направляющим иk = = –tg  = –tg(–) = tg  (см. рис.). Здесь рассмотрен случай k < 0.

Т.о., угловой коэффициент k – это тангенс угла наклона прямой, т.е. угла между прямой и осью абсцисс, отсчитываемого от оси абсцисс до прямой против часовой стрелки. В случае, когда прямая параллельна оси абсцисс или совпадает с ней, угол её наклона считается равным нулю.

Пример. Написать все виды уравнений прямой, делящей стороныAB иAC треугольникаABC в отношении соответственно, еслиA(–5; 6), B(3; –4), C(8; 8) (система координат декартова).

Решение.Прямая проходит через точкиD(; ) иE( ; ) со свойствами(+5; –6)= = (3–; –4–)и(+5; –6) = (8–; 8–). Поэтому и , т.е.D( – ;)иE(;),(;).

Итак, пишем уравнения прямой, проходящей через точку D( – ;)с направляющим векторома(5; 12) || .

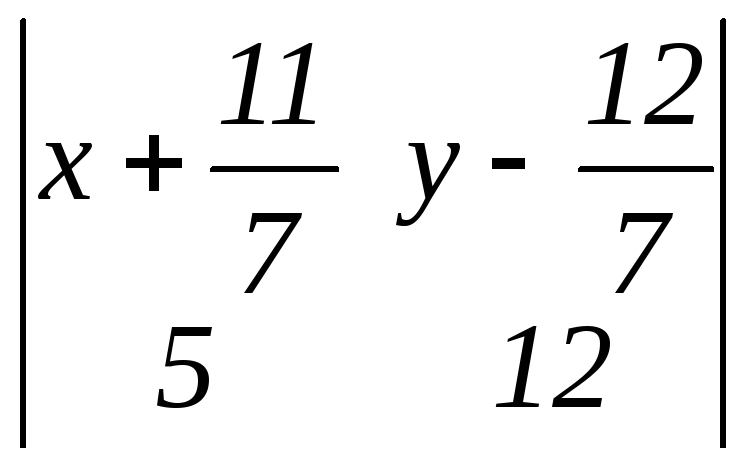1) каноническое уравнение прямой (DE):= или = 0.

2) параметрическое уравнение прямой (DE): , (t  R).

3) общее уравнение прямой (DE): 12(7x+11) = 5(7y–12) или после преобразований84x–35y+192 = 0.

4) уравнение прямой (DE) в отрезках: += 1.

5) нормальное уравнение прямой (DE): x – y+= 0.

6) уравнение прямой (DE)с угловым коэффициентом: y = x + .

Угол между прямыми на плоскости

Пусть на плоскости заданы декартовасистема координат и две прямые l₁ иl₂ с уравнениямиA_ix+B_iy+C_i = 0 (i = 1, 2).

Если эти прямые пересекаются в одной точке, то образуется четыре угла (см. рис.), которые разбиваются на две пары равных вертикальных углов  ии дополняют друг друга до. Наименьший из этих углов называетсяуглом между прямыми l₁ и l₂и обозначается (l₁ , l₂ ). Ясно, что угол между прямыми всегда не превосходит. Если прямые совпадают или параллельны, то угол между ними считается равным0.

1) через направляющие векторы:отложим от точки пересечения направляющие векторыa(–B₁ ; A₁) иb(–B₂ ; A₂). Возможны два основных расположения этих векторов (см. рис.). В первом случае (l₁ , l₂) =  = (a, b), а во втором (l₁ , l₂) = = = – =  – (a, b). Таким образом, если(a, b)  (т.е.cos (a, b)  0), то  (l₁ , l₂) =  = (a, b), cos  (l₁ , l₂) = +cos (a, b) , а если (a, b) > (т.е. cos (a, b) < 0), то  (l₁ , l₂) =  –  =  – (a, b), cos  (l₁ , l₂) = –cos (a, b). В любом случаеcos  (l₁ , l₂) = = | cos (a, b) | и, вспоминая связь косинуса угла между векторами со скалярным произведением и его выражением через координаты, получаем (l₁ , l₂) = arc cos | cos (a, b) | = = arc cos =arc cos . Эта формула работает даже, если прямые совпадают или параллельны. В этом случае векторыa иb коллинеарны, так что величина равна1 (проверьте !!!) и (l₁ , l₂) = arc cos 1 = 0.

2) через угловые коэффициенты:С понятием угла тесно связано понятие углового коэффициента прямой и уравнение прямой с угловым коэффициентом.

Пусть на плоскости заданы две прямые l₁ иl₂ с уравнениямиy = k_ix+b_i (i = 1, 2). Тог­да, как показывает рисунок (рассмотрите все возможности !!), (l₁ , l₂) =  =  –  и

tg = tg(–) = =и  [0; ].Таким образом, получаем: (l₁ , l₂) = arc tg .

Таким образом, доказана

Теорема (о вычислении угла между прямыми).(1) Если прямые l₁ и l₂ заданы в некоторой декартовой системе координат общими уравнениями A_ix+B_iy+C_i = 0 (i = 1, 2), то выполнено равенство

 (l₁ , l₂) = arc cos .

(2) Если прямые l₁ и l₂ заданы в некоторой декартовой системе координат уравнениями с угловыми коэффициентами y = k_ix+b (i = 1, 2), то

 (l₁ , l₂) = arc tg .

Следствие (о перпендикулярности прямых). (1) Если прямые l₁ и l₂ заданы в некоторой декартовой системе координат общими уравнениями A_ix+B_iy+C_i = 0 (i = 1, 2), то они перпендикулярны тогда и только тогда, когда A₁A₂+B₁B₂ = 0.

(2) Если прямые l₁ и l₂ заданы в некоторой декартовой системе координат уравнениями с угловыми коэффициентами y = k_ix+b (i = 1, 2), то они перпендикулярны тогда и только тогда, когда k₁k₂ = –1 .

Доказательство следует из того, что =  cos  = 0  tg  = +∞ .

Расстояние от точки до прямой на плоскости

Будем предполагать, что прямая lзадана нормальным уравнением Ax + By + C = 0, гдеA² + B² = 1 в декартовой системе координат.

На плоскости задана произвольная точка P(x₀ ; y₀) и нужно найти расстояниеd(P, l) от неё до прямойl. Если провести через т.P прямуюl ||l, то искомое расстояние будет равно d(P, l) = HH, гдеOH  l, OH  l.

Переходим к вычислениям. Направляющие векторы прямыхl иl совпадают, поэтому ура­в­не­­ние прямойl записывается в нор­мальном видеAx+By+C = 0, гдеC находится из условия про­хожденияl через точку P : Ax₀+By₀+C = 0, т.е. выполнено равенство C = –(Ax₀+By₀ ) .

При этом, H(–AC; –BC), H(–AC; –BC), (–A(C–C); –B(C–C)) иHH = || === |C – C| = |–(Ax₀+By₀)–C| = = |Ax₀+By₀+C| .

Одновременно получена формула для расстояния d(l, l) между параллельными пря­мыми, заданными нормальными уравнениямиAx+By+C = 0 иAx+By+C = 0:d(l, l) = = |C – C| .

Как изменятся формулы, если прямая задана общим уравнением Ax+By+C = 0 в декартовых координатах ? Нормальное уравнение получается умножением общего уравнения на множитель. Следовательно, все формулы умножатся на этот множитель:d(P, l) = ,d(O, l) = , d(l, l) = .

Подытожим все выводы в теореме:

Теорема (о расстояниях от точки до прямой и между прямыми).Пусть на плоскости даны прямая l с общим уравнением в некоторой декартовой системе координат Ax+By+C = 0 (A²+B²  0) и точка P(x₀ ; y₀ ). Тогда d(P, l) = ; в частности, если Р является началом координат О, то d(О, l) = .

Если уравнением Ax+By+C = 0 задана вторая прямая l, параллельная l, то d(l, l) = .

МЕТОДИКА 22. Прямоугольная система координат на плоскости, абсцисса и ордината точки

Виленкин 6 кл. Тема изучается в 6 классе в большой теме «Координаты на плоскости». Основные понятия: координатные прямые, система координат, абсцисса, ордината.

Типы математических ошибок по данной теме: не различают понятия, такие как абсцисса и ордината, положительные и отрицательные числа, направление положительной оси координат, ошибки при построении точки на плоскости координат.

Учебные задачи на устроение ошибок:

• Постройте точку по ее координатам

• Определите координаты заданной на плоскости точки

• Задания вида «рисуем по координатам»

• Как определить положение точки на прямой, на плоскости

• Как располагаются координатные прямые

• Где лежит точка, если ее абсцисса равно нулю, ордината равна нулю.

Методы и средства проверки знаний и умений учащихся.

Контроль знаний и его типы:

• Внешний (учитель за учеником)

• Взаимный (ученик за учеником)

• Самоконтроль (ученик за собственной деятельностью)

Виды контроля:

• Контроль по конечному результату: пошаговый (контроль за операциями), контроль за установлением определенных параметров деятельности

• По месту в процессе обучения: текущий (в ходе учения), итоговый по теме, по курсу обучения. Текущий может быть: предварительный (установить готовность к обучению), ежедневный, периодический.

• В новых педагогических технологиях рассматриваются следующие виды контроля усвоения знаний и способов деятельности: входной, текущий, итоговый.

Формы контроля:

• Массовый

• Индивидуальный: фронтальный, индивидуальный опрос, контрольные работы, сочинения, диктанты.

Способы контроля: письменный, устный, практический.

Средства контроля: математический диктант, дидактические материалы, карточки, тесты, перфокарты, таблицы, опорные схемы, задания с печатной основой, компьютер, модели и приборы и т.д.

К современным средствам относятся: тест, рейтинговые системы, портфолио (учитывать творческие работы, подходы учащихся).

Фрагмент урока на этапе контроля.

Деятельность учителя	Деятельность учащихся
Ребята, давайте теперь посмотрим как вы усвоили материал. Как построить точку С на координатной плоскости, если ее координаты (–4; 3). Игра “Поражение цели”. Класс делится на две команды: “Наводчики” и “Стрелки”. По очереди каждая команда поражает цель своего противника. Чья команда поразит больше цели!	Необходимо отложить на координатных осях абсциссу и ординату точки С. Абсцисса равна -4, т.е. откладываем от начала координат влево 4 единицы. Ордината равна 3, т.е. откладываем от начала координат три единицы вверх. Мысленно проводим прямые, параллельные осям координат, в данных точках; и точка пересечения этих прямых и является искомой точкой С.

Типы математических ошибок по данной теме: не различают понятия, такие как абсцисса и ордината, положительные и отрицательные числа, направление положительной оси координат, ошибки при построении точки на плоскости координат.

Учебные задачи на устроение ошибок:

• Постройте точку по ее координатам

• Определите координаты заданной на плоскости точки

• Задания вида «рисуем по координатам»

• Как определить положение точки на прямой, на плоскости

• Как располагаются координатные прямые

• Где лежит точка, если ее абсцисса равно нулю, ордината равна нулю.

Методы и средства проверки знаний и умений учащихся.

Контроль знаний и его типы:

• Внешний (учитель за учеником)

• Взаимный (ученик за учеником)

• Самоконтроль (ученик за собственной деятельностью)

Виды контроля:

• Контроль по конечному результату: пошаговый (контроль за операциями), контроль за установлением определенных параметров деятельности

• По месту в процессе обучения: текущий (в ходе учения), итоговый по теме, по курсу обучения. Текущий может быть: предварительный (установить готовность к обучению), ежедневный, периодический.

• В новых педагогических технологиях рассматриваются следующие виды контроля усвоения знаний и способов деятельности: входной, текущий, итоговый.

Формы контроля:

• Массовый

• Индивидуальный: фронтальный, индивидуальный опрос, контрольные работы, сочинения, диктанты.

Способы контроля: письменный, устный, практический.

Средства контроля: математический диктант, дидактические материалы, карточки, тесты, перфокарты, таблицы, опорные схемы, задания с печатной основой, компьютер, модели и приборы и т.д.

К современным средствам относятся: тест, рейтинговые системы, портфолио (учитывать творческие работы, подходы учащихся).

Билет № 23. Плоскость в пространстве.

Пусть в пространстве E₃ задана некоторая аффинная система координат и плоскость .

I. Каноническое уравнение плоскости. Выберем произвольную точку M₀(x₀ ; y₀ ; z₀ )   и от неё отложим любые неколлинеарные векторы a = иb = с концамиM, N  . Тогда плоскость  однозначно определяется тремя точками M₀ , M, N , не лежащими на одной прямой. Если а(; ; ), b( ;  ; ), то для любой точки X(x ; y ; z)  E₃ имеем X     (, a , b компланарны)  ab = 0   = 0 .Это уравнение относительно переменных x, y, z называется каноническим уравнением плоскости  (по аналогии с каноническим уравнением прямой). Векторы a, b называются направляющими векторами плоскости. Поэтому каноническое уравнение плоскости – это уравнение, составленное по координатам одной точки плоскости (M₀  ) и двух её направляющих векторов (а(; ; ), b( ;  ; )).

Ясно, что каноническое уравнение плоскости определено неоднозначно: можно произвольно выбирать точку плоскости и направляющие векторы.

II. Параметрическое уравнение плоскости. Из теории определителей известно, что = 0   s, t  R   s, t  R (здесь важно, что векторы a( ;  ; ) и b( ;  ; ) линейно независимы). Таким образом, получаем параметрическое уравнение плоскости:

, s, t  R

Ясно, что по заданному параметрическому уравнению плоскости без труда выписывается её каноническое уравнение.

III. Общее уравнение плоскости. любая плоскость  может быть задана уравнением Ax+By+Cz+D = 0 (A²+B²+С² 0), которое называется общим уравнением плоскости. Обратно, каждое общее уравнение Ax+By+Cz+D = 0 (A²+B²+С²  0) задаёт в пространстве некоторую плоскость, направляющие векторы а( ;  ; ) и b( ;  ; ) которой являются произвольными линейно независимыми решениями однородного уравнения Ax+By+Cz = 0.

Теорема (об общем уравнении плоскости). (1) Каждая плоскость в пространстве E₃ задаётся некоторым общим уравнением вида Ax+By+Cz+D = 0 (A²+B²+C²  0).

(2) Каждое общее уравнение Ax+By+Cz+D = 0 (A²+B²+C²  0) однозначно определяет некоторую плоскость в пространстве E₃ .

(3) Два общих уравнения плоскости A₁x+B₁y+C₁z+D₁ = 0, A₂x+B₂y+C₂z+D₂ = 0 (A₁²+B₁²+C₁²  0  A₂²+B₂²+C₂²), задают одну и ту же плоскость тогда и только тогда, когда коэффициенты этих уравнений пропорциональны: = = = =   R \ {0}.

(4) При аффинной замене координат общее уравнение плоскости преобразуется снова в общее уравнение плоскости, т.е. вид общего уравнения плоскости инвариантен при аффинных преобразованиях координат.

IV. Уравнение плоскости в отрезках. Пусть плоскость , не проходящая через начало аффинной системы координат и не параллельная ни одной из координатных осей Ox, Oy, Oz, задана общим уравнением Ax+By+Cz+D = 0 (A²+B²+C²  0). Это значит, что A0+B0+C0+D  0, т.е. D  0, и плоскость  пересекает все три координатные оси. Каковы эти точки пересечения ? Координаты точки пересечения с осью Ox удовлетворяют условию   . В частности,A  0. Аналогично находятся и точки пересечения плоскости  с осями Oy и Oz : (0 ; – ; 0), (0 ; 0 ; –)Итак, уравнение плоскости Ax+By+Cz+D = 0 удовлетворяет ограничениям A  0, B  0, C  0, D  0. Тогда Ax + By + Cz+D = 0  Ax + By + Cz = – D  ++= 1  ++= 1, где a = – , b = – , c = – – найденные выше координаты пересечения плоскости с соответствующими координатными осями.

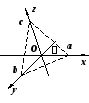
Полученное уравнение ++= 1 называется уравнением плоскости в отрезках. Здесь величины a, b и с определяют отрезки, отсекаемые плоскостью на координатных осях (см. рис).

V. Нормальное уравнение плоскости. Плоскость можно задать уравнением Ax+By+Cz+D = 0, где A²+B²+C² = 1, которое называют нормальным уравнением прямой. Смысл этого названия можно понять, если ввести следующее определение: вектор единичной длины, перепендикулярный к заданной плоскости, называется вектором нормали для этой плоскости.

Рассмотрим вектор n(A; B; C) и исследуем его расположение по отношению к плоскости. Если рассмотреть произвольный вектор , где M(x₁ ; y₁ ; z₁ ), N(x₂ ; y₂ ; z₂ )  , то (x₂ – x₁ ; y₂ – y₁ ; z₂ – z₁ ) и из условий Ax₁+By₁+Cz₁+D = 0, Ax₂+By₂+Cz₂+D = 0 следует, что n=A(x₂ – x₁)+B(y₂ – y₁)+C(z₂ – z₁) = 0. Таким образом, n  и ввиду произвольности точек M, N  , получаем n   . Если плоскость задана нормальным уравнением, то A²+B²+C² = 1, |n| = 1, так что n(A; B; C) – вектор нормали для плоскости, заданной нормальным уравнением Ax+By+Cz+D = 0.

Угол между двумя плоскостями

Пусть в пространстве заданадекартова система координат. Рассмотрим две плоскости ₁ , ₂ с общими уравнениями А_ix+B_iy+C_iz+D_i = 0 (A_i²+B_i²+C_i²  0, i = 1, 2). Эти плоскости либо совпадают, либо параллельны, либо пересекаются по прямой. В первых двух случаях величина угла между ними считается равной нулю. В третьем случае при пересечении плоскостей образуются четыре двугранных угла (см. рис.), они попарно вертикальные, и величина меньшего из них называется углом между плоскостями ₁ и ₂ .

Как вычислять угол между плоскостями ? Рассмотрим прямую l пересечения плоскостей ₁ и ₂ с направляющим вектором a( ;  ; ) и произвольной точкой P(x₀ ; y₀ ; z₀)  l. Тогда величина угла  (₁ , ₂) =  равна углу  (k₁ , k₂) между двумя прямыми k₁ и k₂, перпендикулярными прямой l и проходящими через т. P в плоскостях _i (i = 1, 2). Как было отмечено при выводе нормального уравнения плоскости, для любой плоскости с общим уравнением Ax+By+Cz+D = 0 вектор N(A; B; C) перпендикулярен этой плоскости (т.е. перпендикулярен любому направленному отрезку с концами в этой плоскости). Поэтому для плоскости , проходящей через прямые k₁ , k₂ в качестве вектора N можно взять направляющий вектор a прямой l, перпендикулярный обеим прямым k₁ и k₂ . Таким образом,  имеет общее уравнение вида x+y+z+D = 0, где D = –x₀–y₀–z₀ получается из условия P(x₀ ; y₀ ; z₀)  .

С другой стороны, векторы N_i(A_i ; B_i ; C_i), перпендикулярны плоскостям _i (i = 1, 2), а значит и прямой l. Поэтому плоскость с направляющими векторами N₁ , N₂ и проходящая через т. P совпадает с . Кроме того, из условий N₁  k₁ , N₂  k₂ следует, что углы  (k₁ , k₂) и  (N₁ , N₂) с общей вершиной P в плоскости  имеют соответственно перпендикулярные стороны. Значит либо  =  (k₁ , k₂) =  (N₁ , N₂) и cos  = cos  (N₁ , N₂), либо  =  (k₁ , k₂) =  –  (N₁ , N₂) и cos  = – cos  (N₁ , N₂). В любом случае cos  = = |cos  (N₁ , N₂)| . Таким образом, получены формулы:

Эти формулы справедливы и в случае коллинеарных векторов N₁ , N₂ , т.е. когда плоскости ₁ и ₂ совпадают или параллельны. Особенно просто вычисляется угол между плоскостями, заданными нормальными уравнениями А_ix+B_iy+C_iz+D_i = 0 (A_i²+B_i²+C_i² = 1, i = 1, 2):  (₁ , ₂) = arc cos |A₁A₂+B₁B₂+C₁C₂ |.

Следствие (о перпендикулярности плоскостей). Плоскости ₁ и ₂ , заданные в некоторой декартовой системе координат общими уравнениями А_ix+B_iy+C_iz+D_i = 0 (A_i²+B_i²+C_i²  0), i = 1, 2, перпендикулярны (т.е.  (₁ , ₂) = ) тогда и только тогда, когда A₁A₂+B₁B₂+C₁C₂ = 0.

Двугранный угол — пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями.

Полуплоскости называются гранями двугранного угла, а их общая прямая — ребром.

Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру.

У всякого многогранника, правильного или неправильного, выпуклого или вогнутого, есть двугранный угол на каждом ребре.

Р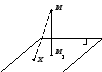асстояние от точки до плоскости. Пусть задана точка M(u; v; w) E₃ и плоскость  с нормальным уравнением Ax+By+Cz+D = 0 (A²+B²+C²= 1). Тогда расстояние (M, ) от точки M до плоскости  – это min{ MX | X  }, и из рисунка видно, что этот минимум достигается при X = M_ (в прямоугольном треугольнике катет короче гипотенузы). Таким образом, (M, ) = MM_ – расстоянию от точки до её проекции на плоскость . Для нахождения этого расстояния воспользуемся результатами вычислений, проведённых при решении задачи § 8. Имеем

M_((1–A²)u–ABv–ACw–AD; –ABu+(1–B²)v–BCw–BD; –ACu–BCv+(1–C²)w–CD).

Поэтому (M, ) = MM_ === = |Au+Bv+Cw+D| .

В общем случае, когда плоскость задана не нормальным, а общим уравнением, для перехода к нормальному уравнению нужно поделить все коэффициенты общего уравнения на . Таким образом, получится формула(M, ) = .

МЕТОДИКА 23. Тема: «Прямоугольная система координат в пространстве»

11кл 10-11 кл.–старшая шк, предметы алг и нач ан и геометрия. М-ды обуч: наглядные(..), практические(реш-ие зазл упр-ий), слов, дидак-ие игры(игр сит-ии); по логике излож–дедук м-ды полн; по степени сам-ти-с/р, исслед-кие м-ды.Обуч: ввести пон прямоуг сист коорд в пр-ве; выраб-ть умение строить т. по задан ее коор-там; выраб ум нах-ть коор-ты т., изображ-ой в задан сист коор-т. Разв: разв мировоз(изуч реал действит-ти сред-ми мат), разв позн-ных проц-в, диалект-го мыш-ия, функц-го стиля мышл, разв общеуч-ые умения (раб с книгой).Восп: восп интерес к мат (истор-ий мат), кул-ру общения, осущ-ть эстет-ое, экол-ое восп-ние, профес-ную ориентацию уч-ся, воспит отд кач лич-ти(аккур, последов-сть, трудолюб, ответственность, настойч-сть и др.)Ур. ознак с нов. мат(цель–ввести понятие и устан св-ва или построить прав); Эт ур:I Орг. мом (сообщ-е темы, ц ур. и мот-ция учеб. деят уч-ся).II Подгот к изуч нов. мат (повт-е, актуализация баз-х З).III Ознак с нов. мат.IV Первич осмыс и закрепл изуч. мат-ла.V Постан д/з.VIПодвед ит ур.При изуч нов мат-ла д/достиж мот-ции м/создать проблем сит-ию, столк уч-ся с труд, кот они не м/раз-ть при пом имеющ у них запаса З; сталк-сь с труд, они убежд в необх получ нов З или прим стар в нов сит. М-ды мотив:1.разнооб виды деят-ти 2.яркость эмоц-ть излож мат 3.подбор посильных зад,созд-ие усл для выбора зад разного ур-ня слож и возм-ть скоррек-ть этот выбор в сл неудачи или успеха 4.оперир-ие ранее изуч мат-ом 5. Индивид оцен-ие В кач-ве сред нагляд м/испол презент MS PowerPoint, различ чертежи, схемы, макеты и табл. Пер изуч темы уч-ся м/прочит небол истор-ую справ.

Цели:

Образовательные: - ввести понятие прямоугольной системы координат в пространстве;

- выработать умение строить точку по заданным ее координатам;

- выработать умение находить координаты точки, изображенной в заданной системе координат.

Развивающие: - развитие мировоззрения;

- развитие логического мышления (в форме понятий, суждений, умозаключений);

- развитие геометрического и абстрактного мышления, речи, памяти.

Воспитательные: - воспитание интереса к математике через задачи, занимательные задачи, дидактические игры;

- воспитание отдельных качеств личности: аккуратности, точности, наблюдательности, самостоятельности.

Тип урока: урок изучения нового материала.

Примерный план урока

1.Перед изучением темы учащимся можно прочитать небольшую историческую справку: прямоугольные употреблялись в геометрии еще до начала нашей эры. Древний математик александрийской школы Апполоний Пергский (живший в III – II вв. до н.э.) уже пользовался прямоугольными координатами.

Впервые идея координатного метода была систематически развита Пьером Ферма и Рене Декартом. В их формулировках расстояния до координатных осей могли быть только положительными числами или нулем. Важная идея о том, что одно или оба эти расстояния можно также считать и отрицательными, принадлежит Исааку Ньютону. Г.В.Лейбниц первым назвал эти расстояния «координатными»

Таким образом, открытие декартовых координат не принадлежит Декарту. Декарт построил аналитическую геометрию, а в ней, как в фокусе, сошлись математические открытия медленно, с трудом слагавшиеся в течение тысячелетий. Работа Декарта «La Geometric», в которой излагались основные идеи аналитической геометрии на плоскости, была опубликована в 1637г.

- Объяснить правило задания прямоугольной системы координат в пространстве: прямоугольная система координат в пространстве задана, если выбрана точка – начало координат, через эту точку проведены три попарно перпендикулярные прямые, на каждой из которых выбрано направление (оно обозначается стрелкой), и задана единица измерения отрезков.

- Используя рис 114 учебника, обратить внимание на обозначения и названия осей координат в пространстве. Сопоставить эти обозначения с соответствующими обозначениями осей координат на плоскости, известными из курсов алгебры и геометрии 7 – 9 классов. (см.: Атанасян Л.С. и др. Геометрия 7-9. М.: Просвещение, 1996 и послед изд.)

- Подчеркнуть, что в прямоугольной системе координат каждой точке М пространства соответствует тройка чисел, которые называются ее координатами. Они определяются аналогично координатам точек на плоскости. Можно привести пример, что любую точку Земли можно полностью охарактеризовать широтой, долготой и высотой над уровнем моря.

Для определения координат точки М в пространстве через эту точку проводят три плоскости, перпендикулярные к осям координат. Затем, используя точки М₁, М₂, М₃ пересечения этих плоскостей с осями координат (рис. 115 учебника), находят координаты точки М.

На уроке полезно выполнить упражнения двух типов: на нахождение координат данной точки по чертежу и на построение точки по заданным ее координатам. Для этого можно использовать рис. 116 учебника. Например, для нахождения координаты точки А на этом рисунке, проводим через данную точку перпендикуляр к плоскости ОXY (обозначим его АА₁), а затем через точку А₁ – перпендикуляры к осям ОХ и OY (обозначим их А₁М₁ и А₁М₂). Основания перпендикуляров (точки М₁ и М₂) дают возможность найти абсциссу и ординату точки А, а длина перпендикуляра АА₁ дает аппликату точки А.

Следует объяснить, почему найденные таким образом абсцисса, ордината и аппликата точки А соответствуют данному выше определению координат точки: плоскость АА₁М₁ перпендикулярна к оси OХ, плоскость АА₁М₂ перпендикулярна к оси OY, а плоскость, проходящая через точку А и перпендикулярная к оси OZ, пересекает ось ОZ в точке М₃, такой, что OM₃=АА₁, поэтому точки М₁, М₂, М₃ и есть те самые точки, которые позволяют найти координаты точки А.

- Необходимо уделить внимание нахождению координат точек, лежащих в координатных плоскостях или на осях координат. Если точка М(x, y, z) лежит в плоскости OYZ, то y=0

- Для закрепления навыков нахождения координат точек и построение точек по их заданным координатам можно дать задания: 1. Построить по координатам; 2. По рисунку найти координаты вершин фигуры.

Например, построить по координатам:

(1; -3; 0)	(-2,5; 5,5; 0)	(5; 4; 0)
(-1; -3; 0)	(-1; 6; 0)	(5,5; 3; 0)
(-2; -2; 0)	(1; 6; 0)	(4; 2; 0)
(-3; -1; 0)	(2,5; 5,5; 0)	(3; 1; 0)
(-3; 1; 0)	(1,5; 5; 0)	(3; -1; 0)
(-2; 2; 0)	(1; 4; 0)	(2; -2; 0)
(-1; 3; 0)	(1; 3; 0)	(1; -3; 0)
(-1; 4; 0)	(2; 2; 0)	(1,5; 5; 0)
(-1,5; 5; 0)	(3; 4; 0)	(-1,5; 5; 0)

Билет № 24.Движение плоскости.

Движением плоскости называется такое ее преобразование, которое сохраняет расстояния между точками (иногда движение называют перемещением). Всякое движение сохраняет длины отрезков, углы между прямыми и площади фигур.

Основные виды движения плоскости:

1. Параллельный перенос.Параллельным переносом плоскости на вектор а называется отображение плоскостиT_a : E₂  E₂ , при котором каждая точка плоскости сдвигается на вектора, т.е.T_a(M) = M, причём = a.

Запишем координатные формулы этого отображения в некоторой декартовой системе координат: если a( ; ), M(x ; y), M(x ; y), то(x –x ; y –y) = a( ; ), откуда находим:

Ясно, что это движение первого рода (с матрицей = ).

2. Поворот.Пусть на плоскости зафиксирована точкаС  Е₂. Отображение плоскостиR_С^ : E₂  E₂ называетсяповоротом с центром в точке С на угол  , если для любой точкиM  E₂ и её образаM = R_С^(M) направленный отрезокполучается из направленного отрезкаповоротом вокруг точкиС на угол . При этом, если  0, то поворот осуществляется против часовой стрелки, а в случае < 0 он выполняется по часовой стрелке.

Зафиксируем на плоскости систему декартовых координат и выведем координатные формулы поворота. Пусть вначале С – начало координат.

Тогда точки M иM лежат на одной окружности с центром в т.О и радиусомR = OM. Поэтомуx² + y² = R², += 1, и значит, на­йдётся такой угол, что = cos  , = sin  , т.е.. Поэтому, и раскрывая по формулам тригонометрии получим:.

Таким образом, получены следующие координатные формулы вращения относительно начала координат:

вращение на угол 

относительно начала координат

В общем случае центр вращения имеет координаты С(x₀ ; y₀ ) . Поэтому поворачивается на угол вектор(x–x₀ ; y–y₀ ) и переходит в вектор(x–x₀ ; y–y₀ ). Подставляя эти координаты в выведенные формулы, получим:

или.

Итак, получены общие формулы вращения на угол  вокруг произвольного центраС(x₀ ; y₀ ):

a = x₀ – x₀cos  + y₀sin  ,

b = y₀ – x₀sin  – y₀cos  .

вращение на угол 

относительно центра С(x₀ ; y₀)

Полученные формулы показывают, что поворот является движением первого рода (с матрицей ).

3. Симметрия относительно точки.Пусть на плоскости задана фиксированная точкаО  E₂ . ОтображениеS_O : E₂  E₂ называетсясимметрией с центром в точке О, если для любой точкиM  E₂ и её образаM = S_O(M) выполняется равенство = –.

Координатные формулы этого преобразования получаются легко: если в некоторой аффинной системе координат O(x₀ ; y₀ ), M(x ; y), M(x ; y) , то(x–x₀ ; y–y₀ ) = = – (x–x₀ ; y–y₀ )   .

Таким образом, получены координатные формулы для симметрии относительно точки:

симметрия с центром О(x₀ ; y₀)

симметрия с центром О(0; 0)

Эти формулы показывают, что симметрия с центром О является движением первого рода (с ортогональной матрицей = ) и совпадает со вращением вокруг т.О на угол (сверьте формулы !!!). Итак,S_O = R_O^ .

4. Симметрия относительно прямой.Пусть на плоскости задана фиксированная прямаяl . ОтображениеS_l : E₂  E₂ называетсясимметрией относительно прямой l, если для любой точкиM  E₂ её образM = S_l(M) симметриченM относительно прямойl . Это значит, что(MM)  l иM симметричнаM относительно точкиP = (MM)  l (см. рис.).

Пусть в некоторой декартовойсистеме координат прямаяl задана общим уравнениемAx+By+C = 0 (A²+B²  0),M(x₀ ; y₀ ). Тогда, как известно,a(–B; A) –нап­равляющий вектор этой прямой, аn(A; B)  a . Поэтому параметрическое уравнение прямой(MM) имеет вид (t  R), и можно найти координаты точки P : A(x₀+At) + B(y₀+Bt) + C = 0  t = – . Таким образом, получаемP(x₀ – A;y₀ – B). Используя выведенные ранее координатные формулы симметрии относительно точкиP, отсюда находим:

M(–x₀ + 2( x₀ – A) ; –y₀ + 2( y₀ – B)) =

= M(;).

Используя привычные обозначения M(x ; y), M(x ; y), получим

симметрия относительно прямой

l: Ax + By + C = 0

симметрия относительно прямой

l: y = 0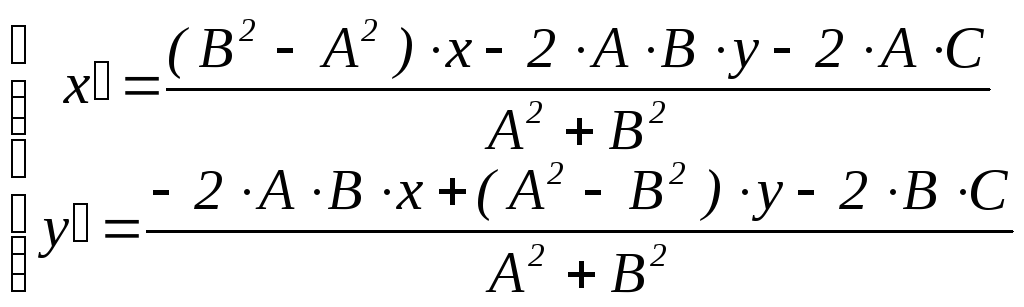

Ясно, что матрица U = этого аффинного преобразования ортогональна и поэтому имеет виддля некоторого угла, определяемого условиями. В частности, для прямойl с уравнениемy = 0 имеемU = = . Таким образом, симметрия S_l относительно прямойl является движениемвторогорода.

5. Скользящая симметрия.Это преобразование плоскостиS_l,v является композицией двух движений – симметрии относительно прямойl и параллельного переноса на вектор, коллинеарный направляющему вектору этой прямой:S_l,v = T_vS_l (см. рис.).

Из рисунка видно, что порядок, в котором берётся композиция преобразований в скользящей симметрии несущественен: T_vS_l = S_lT_v.

Ясно, что скользящая симметрия, будучи композицией движений первого и второго родов, сама будет движением второго рода. Общие координатные формулы скользящей симметрии запишите сами – приведём только формулы для скользящей симметрии относительно оси OX, когда прямаяl задаётся уравнениемy = 0, аv( ; 0):

скользящая симметрия

относительно оси OX

Оказывается, что все движения плоскости исчерпываются частными видами движений, рассмотренными выше.

Можно доказать, что любое движение плоскости является одним из указанных видов, т.е. других движений плоскости не существует. В этом заключается классификация движения.

Теорема (о классификации движений). (1) Любое движение первого рода является либо тождественным преобразованием плоскости, либо параллельным переносом на некоторый вектор, либо поворотом относительно некоторого центра на какой-то угол.

(2) Любое движение второго рода есть либо осевая симметрия (симметрия относительно прямой), либо скользящая симметрия.

(3) Любое движение плоскости есть либо тождественное преобразование плоскости, либо параллельный перенос на некоторый вектор, либо поворот относительно некоторого центра на какой-то угол, либо осевая или скользящая симметрия.

Задача. На плоскости даны прямаяl и две т.AиB. Построить наl т.C, такую, чтобыl являлась биссектрисой.

Построение: 1. Применим осевую симметрию и найдем для т. А симметричную ей т.А^’.

2. Строим прямую ВА’.

3. Находим точку пересечения l(BA’)=C.

4. Строим прямую СА.

В силу осевой симметрии ΔСАО=ΔСА’О против равных сторон лежат равные углы, т.е..

МЕТОДИКА 24.

Образовательные цели урока:

5-6классыпропедевтическоеизучение геометрических преобразований, создается запас наглядных представлений о симметричных фигурах.

Основной курс,8 класс тема «Преобразование фигур» (смотри программу). В учебных пособиях по геометрии эта линия представлена по-разному: так в учебнике А.В.Погорелова «Геометрия 7-11» геометрические преобразования являются лишь объектами изучения. Основное внимание уделяется преобразованию подобия: тема - подобие треугольников.

10-11 классы - изучаются преобразования в пространстве - симметрия относительно плоскости.

Цели изучения темы:

Обучающие: знать основные понятия, определение преобразований: симметрии, подобия, подобных треугольников; свойства преобразований, доказательство этих свойств, суть метода преобразований; уметьприменять преобразования при решении задач.

Развивающие цели:развитие диалектического мировоззрения: показать связь геометрических преобразований с окружающей действительностью. Развитие логического мышления (в форме понятий, суждений, умозаключений), развитие пространственных представлений и пространственного воображения, так как геометрические преобразования связаны с созданием образа, развитие конструктивных умений и навыков.

Воспитательные цели:воспитание интереса к математике, например, знакомство с различными геометриями. Воспитание отдельных качеств личности: аккуратности, точности, наблюдательности, эстетическое воспитание. Ипрактические цели:показать использование преобразований при решении прикладных задач, например, использование подобия: определение высоты недоступного предмета.

III. Основные положения методики.Само понятие «геометрическое преобразование» и виды преобразований в школьном курсе математики проходит три этапа (как и все понятия):

1) 5-6 классы пропедевтический курс: используются наглядные, практические методы, игровые ситуации (пример: какая из фигур самая симметричная?мысленно установить, сколько осей симметрии имеет каждая фигура.

2) Основной курсгеометрии 7-9 классы, изучаются определения преобразований, свойства, доказательства свойств. Используются словесные методы обучения, методы дедукции при сохранении наглядных и практических методов, используется метод координат (математический метод).

3) Закрепление (усвоение) понятий: решение задач, доказательства теорем методом геометрических преобразований. Методы обучения зависят от возраста учащихся, от содержания материала, от этапа усвоения.

Привести пример изучения симметрии относительно точки из учебника «Геометрия 7-11» Погорелова А.В. § 9.

IV. Основные типы задач:

Математические задачи:

1) Построить фигуру с помощью данного преобразования (точку, отрезок, треугольник);

2) Доказать равенство или подобие фигур с помощью преобразований;

3) Доказать какие-либо свойства фигур с помощью преобразований;

4) Решить задачу на построение методом геометрического преобразования.

Учебные задачи:отрабатывать определения, формулировки теорем, методы доказательства, формировать метод геометрических преобразований.

Средства наглядности:Выбор наглядности зависит от возраста, содержания учебного материала.

Виды наглядности:

• Предметная (восприятие конкретных предметов, опыт, экскурсии).

• Изобразительная (собственно-изобразительная – конкретные рисунки, символическая – чертежи, схемы, таблицы).

• Словесная (живая речь учителя).

На данном уроке изучения нового материала можно использовать ИД, где показывают презентации (PP) о движении, поворот, то есть основные понятия.

Мотивация:

Необходимое условие – для создания у учащихся интереса к содержанию обучения и к самой учебной де­ятельности — возможность проявить в учении умственную самостоятельность и инициативность. Чем активнее методы обучения, тем легче заинтересовать ими учащихся. Основное средство воспитания устой­чивого интереса к учению — использование таких вопросов и заданий, решение которых требует от учащихся активной поисковой деятельности.

Большую роль в формировании интереса к учению играет создание проблемной ситуации, столкновение учащихся с трудностью, которую они не могут разре­шить при помощи имеющегося у них запаса знаний; сталкиваясь с трудностью, они убеждаются в необходимости получения новых знаний или применения старых в новой ситуации.. Интересна только та работа, которая требует постоянного напряжения. Легкий материал, не требующий умственного напряжения, не вызывает интереса. Преодоление трудностей в учебной деятельности — важнейшее условие возникновения интереса к ней. Трудность учебного материала и учебной задачи приводит к повышению интереса только тогда, когда эта трудность посильна, преодолима, в противном случае интерес быстро падает.

Данная тема изучается в восьмом классе (Погорелов 7-11), с точки зрения психологии, это подростковый период. Для него характерно: парадоксальный характер, мотивация учения снижена, избирательность интересов, формирование новых форм зрелой мотивации, имеет большое значение положение подростка в классе.

2. Фрагмент урока изучения новой темы: «Движение. Свойства движения».

Цели урока:

Образовательные:

Обучающие: обеспечить в ходе урока усвоения понятий «преобразование», «движение», свойства движения, формировать умение применять преобразования при решении задач, формировать умение изображать на плоскости, формировать умение переводить движением фигуру в фигуру.

Развивающие: способствовать развитию логического мышления, восприятия, памяти, внимания, диалектического мировоззрения, показать связь геометрических преобразований с окружающей действительностью, способствовать развитию пространственных представлений и пространственного воображения, так как геометрические преобразования связаны с созданием образа, развитию конструктивных умений и навыков.

Воспитательные: воспитывать устойчивый интерес к математике, воспитывать отдельные качества личности: настойчивость, трудолюбие.

Тип урока: изучение нового материала

Структура урока:

1. организационный момент

2. постановка целей урока

3. проверка домашнего задания

4. подготовка к изучению нового материала

5. изучение нового материала

6. первичное закрепление и осмысление нового материала

7. постановка домашнего задания

8. подведение итогов урока

Действия учителя	Действия учеников
Здравствуйте, ребята! Садитесь. Ответьте на вопросы: 1. Что называется расстояние между точками? 2. Как вычисляется расстояние между точками? Сегодня мы изучим новое понятие «движение» и его свойства.

Билет № 25.

Важной фигурой в геом. Евклида является многоугольник.

Рассмотрим 2 прямые а и в. Эти прямые делят плоскость на две полуплоскости (каждая из них). Предположим, что т.А = а∩в. Выберем некоторый угол.

Как известно, угол является частью плоскости и определяется как пересечение соответствующих полуплоскостей. Рассм. некот. выпуклую замкнутую линию.

Замкнутая линия наз. выпуклой, если для любого его звена а_i все остальные звенья этой ломаной лежат в одной полуплоскости относительно этого звена.

Простая замкнутая(концы совпадают)ломаная наз. многоугольником, если ее соседние звенья не лежат на одной прямой. Звенья ломаной наз. сторонами мног-ка, а т., в кот. пересекаются эти звенья – вершинами многоуг-ка.

Рассмотрим вопрос о величине многоуг-ка. Под величиной многоуг-ка понимают площадь. Мн-во всех многоуг-ков обозн. М. сами многоуг. бедем обозн. латинскими буквами.

Рас-м отображение F:M®R⁺, каждому мн-ву ставит в соотв. некоторое строго положит-ное действит-ное число (R⁺) Отображение F наз. ф-цией площади, заданной на мн-ве М, если отображение F:M®R⁺, удовлетв. требованиям:

1.если А=В, то F(A) = F(B)

2.если С разбит на 2 многоуг. А и В без общих внутр (.), то F(C)=F(A)+F(B)

3. если А явл. единичным кв-том, т.е. кв-том у кот. сторона º1, то F(A) =1

Число F(М)=Sм и наз. площадью многоуг m.

$ет ли f-ия площади на мн-ве многог-ов М, если $ет, то однозначно ли она определяется?

Предположим вначале, что f-ия площади F $ет, т.е. каждому многоугольнику М в соотв. став-ся число Sм, к-ое наз. его площадью (М® Sм)

Виды многоугольников. Прямоугольник со сторонами а и b.

Разделим М вертик. чертой на 2 прямоуг. А и В

М

A B

b a1 a2

Sм = F(M) = F(a,b) S_А= F(a₁,b); Sв= F(a₂,b)

По 2° f-ции площÞ F (М) = F(A) + F(B) Þ F(a,b) = F(a₁,b) + F (a₂,b) ,т.к а=a₁+a₂Þ F(a₁+a₂,b) = F(a₁,b) + F(a₂,b) (1)

1. фун-ция F явл. линейной по первому арг. а.

Аналогично разбиваем М горизон.пр. Þ F(a,b₁+b₂)=F(a,b₁)+F(a,b₂) (2)

2. т.о. f-ия явл. линией по обоим своим арг. т.е. явл. линейной. В теории f-ий док-ся, что всякая линейная f-ия от 2х агр. Имеет след. вид F(x,y)=k x y (3) т.о. Sм= k x y (4)

Воспользовавшись 3° f-ии S: Предположим что М явл. ед.квадратом, т.е. a=b=1, т.к. S=1Þ из (4) Þ1=k*1*1Þ k =1.т.о. (4) принимает окончат-ый вид Sм= ab (I) т.о. Sпрямоуг = произвед. его сторон

Параллелограмм с основанием а и высотой h.

Рас-м прямоуг. KNCD. Легко док-ть, что ∆AKD≡∆BNCÞAK=BNÞKN=aÞ S_KNCD=ah (5) с др.стороны и АВСD, и KNCDсостоит из 2х одинаковых частей: ∆AKD (∆BNC); многоугольник KВСD. Применим 1°и 2°Þ S_АВCD =S_KNCDÞ S=ah (II)

М-∆ с основанием а и высотой h (III)

Произвольный многоугольник Разобьем его к.-либо образом на ∆-ки, измерим S каждого из полученных ∆-ков по (III)и возьмем сумму этих S.Эта сумма и наз.площдью мног-ника М

Зам-е: S многогранника М не зависит от способа его разбиения.

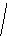
Идея доказательства следующая:S_А = S_А1 + S_А2;

А1S_А = S_В1 + S_В2.

А2 В1 В2

Объединив 2 разбиения, получим более мелкое разбиение многоуг-ка М:

Ŝ_А = (S_С2 + S_С3) + (S_С1 + S_С4) = (S_С1 + S_С2) + (S_С3 + S_С4) = S_А1 + S_А2 = S_АÞŜ_А = S_А

Из всего выше сказанного след., что если функция площади F на мн-ве многоуг-в М существует. То она опред-я единственным образом.

Д-м теперь, что ф-ция площади М существует.

Рассм. произв-й мн-к А, разобъем его каким-либо образом на треуг. (А1,А2,…,Аn). S каждого опред-м по (III)

S_А = (IV) – построенная функция удовлетворяет всем 3м требованиям опре-я площади.

Учитывая все сказанное можно сформулировать след. Т:

Теорема(Существование и единственность функции площади)

На мн-ве мног-ков М в евкл. геомет., ф-ция площади сущ-ет и определена единств. образом.

Два многоугольника называются равновеликими , когда их площади равны.

Два мног-ника наз. равносоставленными, если они состоят из одного и того же набора (множества)треугольников.

Теорема: Из равносоставленности двух мног-ков следует их равновеликость ( и наоборот).

Вывод: Из равновеликости двух многогранников не следует их равносоставленность (каждый многогранник можно разбить на тетраэдры).

МЕТОДИКА 25.Урок обобщения и систематизации знаний

Вид учебных занятий: семинар, конференция.

Цель - усвоение знаний в их системе.

Подготовка учащихся: сообщение заранее темы (проблемы) вопросов, литературы. Вооружение учащихся во время обобщающей деятельности на уроке необходимым материалом: таблицами, справочниками, наглядными пособиями, обобщающими схемами, фрагментами фильмов. Самое главное в методике обобщения - включение части в целое. На уроках обобщения и систематизации знаний выделяют наиболее общие и существенные понятия, законы и закономерности, основные теории и ведущие идеи, устанавливают причинно-следственные и другие связи и отношения между важнейшими явлениями, процессами, событиями, усваивают широкие категории понятий и их систем и наиболее общие закономерности. Процесс обобщения и систематизации знаний предполагает такую последовательность действий: от восприятия, осмысления и обобщения отдельных фактов к формированию понятии, их категорий и систем, от них - к усвоению более сложной системы знаний: овладение основными теориями и ведущими идеями изучаемого предмета. В связи с этим, в уроке обобщения и систематизации знаний выделяют следующие структурные элементы:

1. постановка цели урока и мотивация учебной деятельности учащихся;

2. воспроизведение и коррекция опорных знаний

3. повторение и анализ основных фактов, событий, явлений;

4. обобщение и систематизация понятий, усвоение системы знаний и их применение для объяснения новых фактов и выполнения практических заданий;

5. усвоение ведущих идей и основных теорий на основе широкой систематизации знаний;

6.      подведение итогов урока.

МЕТОДЫ:Беседа,Лекци,Работа с учебником.Схематические рисунки,Лабораторные и практические работыДля более успешного выполнения учащимися подобных заданий некоторые учителя практикуют составление учащимися сравнительных таблиц по предварительно разработанной схеме инструкций, в которой сформулирована последовательность выполнения задания на сравнение и обобщение. Подобные задания могут выполняться и устно. Они способствуют повышению эффективности обобщения и систематизации знаний, заготовке необходимых схем инструкций, моделей, образцов, таблиц. Важное значение имеет предупреждение ошибок в знаниях учащихся и своевременное их исправление.

ФРАГМЕНТ УРОКА

Тема урока: Площадь треугольника.

Тип урока: Урок обобщения и систематизации знаний

Цели урока:

Обучающие: обобщить знания о площади треугольника, закрепить умение решать геометрические задачи на нахождение площади произвольного треугольника, совершенствовать навыки решения задач на применение формул вычисления площадей треугольника.

Развивающие: развивать мышление, речь, память, умение выделять главное, приводить примеры.

Воспитательные: воспитывать общую культуру, активность, самостоятельность, интерес к математике.

Ход урока

3. Обобщение и систематизация понятий, усвоение системы знаний и их применение для объяснения новых фактов и выполнения практических заданий (аукцион – распродажа геометрических фигур (треугольников) и задач о нахождении их площадей).

Вступительное слово учителя.

Сегодня у нас состоится аукцион – распродажа геометрических фигур (треугольников) и задач о нахождении их площадей.Что такое аукцион дословно?Аукцион – это публичная продажа имущества, при которой покупателем становится тот, кто предложит более высокую цену. Участники аукциона называются аукционерами, а человек, проводящий аукцион, – аукционистом.Итак, к нам на аукцион поступило несколько фигур.Условие: кто сразу даст точное определение фигуры, тот ее и покупает. Если у кого-то будут дополняющие ответы, то фигура продается тому, кто закончит полный ответ. Так что постарайтесь дать сразу точный ответ.Желающие ответить (т.е. купить фигуру) поднимают руку. Кто первый поднимет – тот и начинает.

Аукционист после каждого неполного ответа будет ударять в гонг до трех раз, пока не появится ученик (аукционер), желающий дополнить.

Замечание. Если все же ученик, желающий дополнить, не найдется, т.е. задание вызовет у учащихся затруднения, фигуру придется продать предыдущему покупателю. Однако в этом случае учителю следует дополнить ответ самому, чтобы не оставлять пробелов в знаниях.

При продаже фигур № 10, 11, 12, 13, 14 равенство треугольников целесообразно записывать на доске, чтобы учащиеся еще раз могли проследить соответствие равных углов и равных сторон. Для этой цели учителю можно взять помощника из числа учеников. Тот же помощник может во время всего аукциона помогать учителю (аукционисту) замечать, кто первым поднял руку для ответа. В качестве помощника можно взять самого слабого ученика, чтобы, во-первых, и его вовлечь в процесс, во-вторых, придать ему значимость в глазах товарищей.

Если для ответа одновременно поднимают руку несколько человек, следует разнообразить вызов учащихся, чтобы как можно больше ребят вовлечь в работу аукциона.

Все фигуры, выставляемые на продажу, можно нарисовать на отдельных альбомных листах или вырезать из плотной бумаги и ярко раскрасить (и треугольники, и окружности, и пары треугольников).

Аукцион

1. На продажу выставляется произвольный треугольник.

Дать определение треугольника.

Ответ: треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, соединенных отрезками.

2. Продается площадь.

Дать определение.

3. Какую формулу лучше использовать при нахождении площади треугольника.

Задачи (по уровням).

1. Основание треугольника 12 см, его высота – 7 см. Найти площадь треугольника.

2. Катеты прямоугольного треугольника 5 см и6 см. Найти его площадь.

3. Основание треугольника 9 см, а угол между ним и боковой стороной, равной 8 см, равен 30 градусов. Найти площадь треугольника.

1. В прямоугольном треугольнике KMN медиана NP = 10см, а его площадь равна 280 кв. см. Найдите расстояние от середины катета NK до гипотенузы КМ. (При решении этой задачи необходимо помнить, что понятие окружности, описанной около треугольника, учащимся еще неизвестно. В этом случае можно воспользоваться свойствами средней линии треугольника и параллельных прямых).

2. Основание треугольника 12 см. Проекция боковой стороны на основание равна 5 см. Найти площадь треугольника, если известно, что угол между данной боковой стороной и ее проекцией равен 45 градусов.

1. Проекции боковых сторон треугольника равны 6см. Найти площадь треугольника, если один из острых углов этого треугольника равен 45 градусов. (Задачу решить двумя способами).

2. В треугольнике две стороны равны 2см и 4 см. Высота треугольника, проведенная на меньшую из данных сторон, равна 5 см. Что можно сказать о величине высоты, проведенной на большую сторону? Найдите эту высоту.

3. Выразите площадь треугольника через его стороны а, b, с и радиус вписанной окружности r. Сделайте чертеж к задаче.

Билет № 26. Теорема Дезарга.

В проективной геометрии фигуры называются конфигурациями.

Рассмотрим на проективной плоскости P₂три точкиA,B,C, не лежащие на одной прямой. Соединим эти точки прямыми. Полученная конфигурация называется трехвершинником (в элементарной геометрии - треугольник). ТочкиA,B,C– вершины, а прямые, их соединяющие, называются сторонами.

Рассмотрим два трехвершинника, которые могут располагаться в одной плоскости, а могут и не располагаться (обозначим Δ, т.е. ΔABCΔA’B’C’). Имеет место следующая теорема.

Теорема Дезарга (прямая).Если три прямые, соединяющие соответствующие вершины двух трехвершинников, пересекаются в одной точке, то соответствующие стороны этих трехвершинников пересекаются в трех точках, лежащих на одной прямой.

Док-во: Вектор, порождающий некоторую точку проективной плоскости будем обозначать.

Если три точки колинеарны (т.е. лежат на одной прямой) то они порождаются тремя компланарными векторами (т.е. линейнозависимыми).

Рассмотрим три точкиA,A’,S. Эти точки колинеарнывекторы, их порождающие,,­­­­­– линейнозависимые (т.е. один из этих векторов выражается через два других). Тоже самое относится к тройкам точекB,B’,SиC’,C,S. Т.о. имеем три векторных равенства:

Сравнивая равенства системы (1) получаем:

(из 1 и 2)

(из 2 и 3)

(из 1 и 3)

Введем следующие обозначения

Из системы (2) имеем,,(4)

Из системы (3) имеем: точка P(AB), точкаP’(A’B’)

точка T(AC), точкаT’(A’C’) (5)

точка R(BC), точкаR’(B’C’)

Учитывая равенство (4) получаем равенство точек P=P’,T=T’,R=R’. (6)

P=M,T=N,R=K(7)

Пользуясь равенством (3) имеемI

II

I

Выполним следующие операции I-II+III().

(8)

Перепишем (8) в следующем виде (9)

Равенство (9) показывает, что точки M,N,K– колинеарны, т.е. лежат на одной прямойl.

Теорема (об­ратная). Если прямые, соединяющие соответственные вершины трехвершинников АВС и А'В'С", сходятся в одной точке, то соот­ветственные стороны этих трехвершинников пересекаются в точ­ках, лежащих на одной прямой (существен лишь тот случай, когда трехвершинники АВС и А'В'С' лежат в одной плоскости).

По другому теорема звучит так:

Если два трехвершинника имеют центр перспективы, то они имеют и ось перспективы, и наоборот.

Применение теоремы Дезарга в школьных задачах

Применение теоремы Дезарга в планиметрических задачах основано на интерпретации трёхвершинника проективной плоскости в виде обычного треугольника на евклидовой плоскости. Теорему Дезарга в этом случае можно сформулировать так:

Теорема Дезарга. Пусть на плоскости заданы два треугольника А₁В₁С₁ и А₂В₂С₂ , соответствующие вершины которых не совпадают и соответствующие стороны не параллельны. Тогда прямые (А₁А₂), (В₁В₂) и (С₁С₂) пересекаются в одной точке тогда и только тогда, когда три точки АВ = (А₁В₁)  (А₂В₂), ВС = (В₁С₁)  (В₂С₂) и АС = (А₁С₁)  (А₂С₂) лежат на одной прямой.

Задача 1. На плоскости заданы два отрезка прямых и точка. С помощью одной линейки провести прямую, проходящую через эту точку и недоступную точку пересечения данных прямых.

Решение: I. Анализ. Пусть заданы отрезки прямыхl , m и точкаР. Предположим, что уже проведена искомая прямаях = (PR). Её можно постараться интерпретировать как ось перспективы некоторых двух трёхвершинников, у которыхР = (A₁C₁)  (A₂C₂) иR = (A₁B₁)  (A₂B₂), найти точкуQ = (B₁C₁)  (B₂C₂)и провести прямуюх = (PQ).

II. Построение. 1) Произвольно выбираем в доступной части плоскости т.S;

2. проводим три прямые b, c, a, одна из которых (именноb) проходит через т.Р, и все три пересекаются в т.S, получая точкиА₁ = a  l , В₁ = b  l иА₂ = a  m, В₂ = b  m;

3. проводим (А₁Р), получая т.С₁= (A₁P)  c, и(А₂Р), получая т.С₂ = (A₂P)  c;

4. (В₁С₁)  (В₂С₂) = Q ;

5. x = (PQ). S

A₁

l B₁

С₁

R

x Q P

A₂ B₂

m С₂

III. Доказательство.Теорема Дезарга.

IV. Исследование.Задача всегда имеет единственное решение (даже если исходные прямые были параллельны).

МЕТОДИКА 26. Тема: «Основные задачи на построение с помощью циркуля и линейки»

Решить задачу на построение– это значит найти способ построения фигуры, осуществить это построение и доказать, что построенная фигура – фигура, обладающая требуемыми свойствами.

Для начала мы должны описать, что можно делать с помощью линейки и циркуля.

Линейка – инструмент, позволяющий: провести произвольную прямую; провести прямую (произвольную), проходящую через данную точку; провести прямую, проходящую через две данные точки; построить произвольный луч; построить произвольный луч с заданным началом; построить луч с заданным началом, проходящий через заданную точку; построить отрезок с заданными концами.

Циркуль – инструмент, позволяющий: построить произвольную окружность; построить окружность с заданным радиусом; построить окружность с заданным центром и радиусом; отложить данный отрезок на прямой от данной точки.

Цель:Рассмотреть алгоритм основных задач на построение с помощью циркуля и линейки: деление отрезка пополам, построение перпендикуляра к данной прямой.

Общий прием решения задач на основе деятельностного подхода

1. Изучить содержание задачи.

2. Проверить (вспомнить), есть ли общий прием (алгоритм, правило) решения задач такого типа (если «да» - использовать его, если «нет» - п.3).

3. Провести общий или специальный анализ-поиск решения.

4. На основе анализа или известного приема (алгоритма) составить план решения данной задачи.

5. Решить задачу по составленному плану.

6. Записать решение с использованием соответствующей символики.

7. Если нужно, проверить или исследовать решение.

8. Рассмотреть другие возможные способы решения, выбрать наиболее рациональный.

9. Записать ответ.

Обобщенный прием решения задач на построение

1. Анализ: на этом этапе предполагается, что задача решена, т.е. искомая фигура построена. Находятся связи между элементами фигуры и данными задачи.

2. Построение: на этом этапе дается алгоритм построения искомой фигуры, при этом используются данные анализа.

3. Доказательство: на том этапе доказывается, что построенная фигура действительно является искомой фигурой.

4. Исследование: изучается вопрос о том всегда ли задача имеет решение и сколько имеет решений.

Урок закрепления знаний (структура)

1. Проверка д.з., уточнение направлений актуализации изучения материала.

2. Сообщение темы, целей и задач урока, мотивация учения.

3. Воспроизведение изученного и его применение в стандартных условиях.

4. Применение приобретенных знаний в новых или измененных условиях.

5. Подведение итогов урока.

6. Постановка д.з.

Билет № 27. Метрические свойства поверхности.

Понятие гладкой поверхности.

Рассмотрим вектор-функцию двух скалярных аргументов (1). Областью определенияD функции (1), т.е. областью изменения параметров (U,V) является некоторая область плоскости с координатными линиями U и V.

Предположим, что в трехмерном пространствеE₃ задана прямоугольная система координат . Договоримся все векторы откладывать от начала координат в т.О. Если параметр (U,V) изменяется в области D, то т.М описывает в пространстве некоторое множество V.

Опр. Множество VE₃, заданное вектор-функцией (1) называется гладкой поверхностью, если вектор-функция (1) удовлетворяет следующим двум условиям:

1. функция имеет частные производные любого порядка;

2. для любых значений (U,V) первая производная ,линейно независимыми, т.е. являются не коллинеарными векторами. (не параллельны)

В координатной записи вектор-функция .

Ведем следующие обозначения : ,

Вектор-функция (1) имеет полный дифференциал .

Приведем пример гладкой поверхности: рассмотрим обычную плоскость π, заданную начальной точкойM₀, двумя направляющими векторами ,(непараллельные).

Выберем на π произвольно т.М. . Имеем равенство. Окончательно получаем параметрическое уравнение плоскости π:(2)

Проверим выполнимость двух требований:

1. очевидно выполняется, т.к. функция (2) является простейшей линейной функцией;

2. , .

По условию векторы ,- направляющиене коллинеарныене параллельны.

Можно сделать вывод, что обычная плоскость является примером гладкой поверхности.

Первая квадратичная форма поверхности и ее роль.

Рассмотрим поверхность V:

Имеем ,,. Рассмотрим следующие скалярные произведения. Введем следующие обозначения:, , . (3)

Учитывая обозначения (3) получаем (4)

Выражение, стоящее в правой части равенства (4) представляет собой многочлен второй степени относительно переменных (дифференциалов dU, dV). В курсе алгебры такие многочлены называются квадратичными формами.

Квадратичная форма (4) называется первой квадратичной формой поверхности V.

(5)

Величины g₁₁, g₁₂, g₂₂, найденные по правилу (3) являются коэффициентами формы

Очевидно, чтобы найти необходимо и достаточно найти ее коэффициенты по формуле (3).

Рассмотрим значение первой квадратичной формы :

1. длина линии на поверхности.Рассмотрим на поверхности V, заданной уравнением (1), гладкую линию γ, заданную параметрическим уравнением в криволинейных координатах: 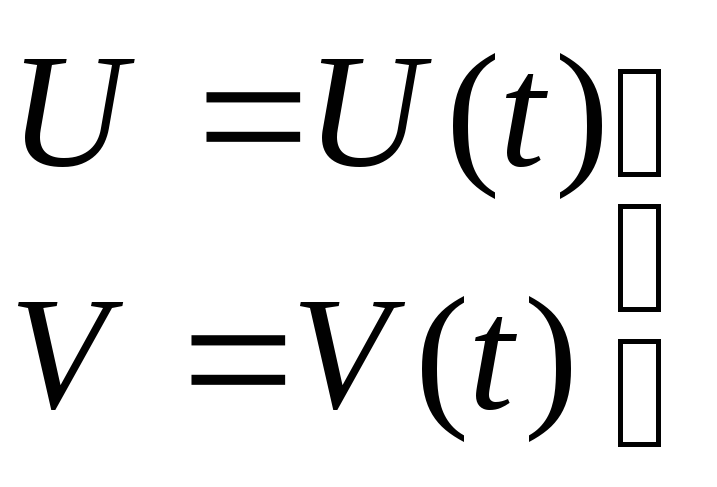(6)

Рассмотрим две точки А(t₁), B(t₂). Найдем длину . Её дифференциал. Переходя к интегралу проводя элементарные выкладки, используя уравнения (6) получаем:.

Итак, первая квадратичная форма позволяет вычислить длину дуги гладкой линии, лежащей на поверхностиV.

2) угол между линиями на поверхности. На поверхности V, заданной уравнением (1) рассмотрим две гладкие линии γ₁ и γ₂, которые пересекаются в некоторой точке М₀. Как известно углом между линиями называется угол между касательными к этим линиям в точке пересечения. Дифференцирование вдоль линии γ₁ будем обозначать d, а вдоль линии γ₂ будем обозначать δ. Т.о. в т.М₀ имеем касательные векторы к линии γ_{1 - ,}к линии γ₂ - .(7)

, т.к. в геометрии угол между линиями считается не тупым, то получаем след. формулу: (8)

Воспользуемся формулами (7), чтобы расписать (8) подробно.

2) площадь поверхности. Выберем на поверхности V точку М(U,V). В области D, которая является областью изменения параметров U,V, точке М соответствует . ПараметруU дадим приращение dU, V – приращение dV. В плоской области D получим прямоугольник . На поверхностиVэтому прямоугольнику соответствует криволинейный четырехугольник.

Вт.М рассмотрим дифференциалы вектор-функции, т.к. изображение линии на поверхностиV яв-ся координатными, то дифференциалы вдоль этих линий имеют такой вид: ,.

На указанных векторах как на сторонах построим параллелограмм, который располагается в касательной плоскости к поверхности V в т.M. Площадь поверхности (V) (S_(v)) некоторое число. Из курса мат.анализа известно, что для вычисления некоторой величины нужно найти ее дифференциал, а затем перейти к интегралу. Очевидно: дифференциал S(V) есть площадь бесконечно малой области поверхности V. Т.о. (9)

Применяя известные формулы аналитической геометрии . Переходя к двойному интегралу получаем следующую формулу для вычисления поверхностиV: (10)

Воспользуемся известной формулой: (11)

Подставляем (10) в (11) получаем:

Из всего сказанного видно, что первая квадратичная форма к поверхностиV позволяет вычислять:

1. длину линии на поверхности;

2. угол между линиями на поверхности;

3. площадь поверхности.

Другими словами: форма позволяет проводить измерения на поверхности, т.е. определяет всю метрику поверхности. Поэтому формаиначе называют основной или метрической формой поверхностиV.

МЕТОДИКА 27.10кл 10-11кл.–старшая шк, предметы алгебра и начала анализа и геометрия.

Методы обуч: наглядные(..), практические(реш-ие зазл упр-ий), словесные, дидак-ие игры(игровые ситуации); по логике излож–дедук м-ды полн; по степени сам-ти-с/р, исслед-кие м-ды.

Юнош-ий возр-т: интелектуал-е воспр-е, символьная нагляд-сть

Цели:

Обуч: ввести пон …; передать уч-ся опред сист матем-х ЗУН. Помочь уч-ся овлад матем-ми идеями, выработать У реш осн типы матем зад, прим-ть теорию на прак.

Разв: разв мировоз(изуч реал действит-ти сред-ми мат), разв позн-ных проц-в, диалект-го мыш-ия, функц-го стиля мышл, разв общеуч-ые умения (раб с книгой).

Восп: восп интерес к мат (истор-ий мат), кул-ру общения, осущ-ть эстет-ое, экол-ое восп-ние, профес-ную ориентацию уч-ся, воспит отд кач лич-ти(аккур, последов-сть, трудолюб, ответственность, настойч-сть и др.)

Урок ознакомления с новым материалом(цель–ввести понятие и устан св-ва или построить прав);

Эт ур:I Орг. мом (сообщ-е темы, ц ур. и мот-ция учеб. деят уч-ся).

II Подгот к изуч нов. мат (повт-е, актуализация баз-х З).

III Ознак с нов. мат.

IV Первич осмыс и закрепл изуч. мат-ла.

V Постан д/з.

VIПодвед ит ур.

Мет-ка изуч пон. 1 Эт – подгот. На нём происх воспр-ие мат-ла, и возник представ-ия, так же н/о показ необх-сть изуч вновь вводим-х пон. Метод-кие приёмы: наблюд, опыт, прак-кая раб, истор-кий обзор, подвод задачи.

2 Эт – основной – определение понятий. Метод-кие приёмы: выявить лог-кую стр-ру опр-ия (термин, род, вид); сформул-ть опр; мотив-ть термин; частные и общие сл понятия; упраж «подведите под понятие»; вывед след-ий; др опр; нахож-е ошибок.

3 Эт – усв пон. Методич. приёмы: установ связь с др. понят; вкл. в клас-цию; провести клас-цию; состав родосл-ую понятия; реш. зад на прим-ие пон; упраж на обобщение и специализацию.

1эт-рассматр-ся зад, привод к опр(по аналогии с кабин)

2эт- термин:угол между прям и пл-тью;род:угол?;видовое отличие:…

3эт-усвоение понятия…классификация:…

В кач-ве средства наглядности м/испол. през MS PowerPoint, различ черт, схемы, макеты и табл.

Билет № 28. Векторное построение геометрии.