1) Вычисление площади плоских фигур.

а) Пусть дана криволинейная трапеция

-если f(x) ≥0

- если f(x) ≤0

б) Если f(x)₂ ≥ f(x)₁, то

в)

г) Пусть кривая задана параметрическими

уравнениями: АВ,

2) Вычисление объёмов тел вращения.

а) Пусть дана криволинейная трапеция, стоящая на оси Ох, будем вращать её вокруг оси Ох.

Пусть дана криволинейная трапеция, стоящая на оси Оу, будем вращать её вокруг оси Оу.

б)

, если

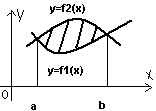
3) Вычисление дуги кривой линии.

Длина отрезка вычисляется по формулам:1. и 2.

Теорема: Если ф-ция f(x) и её производная непрерывна на отрезке [a,b], то длина кривой (дуги): 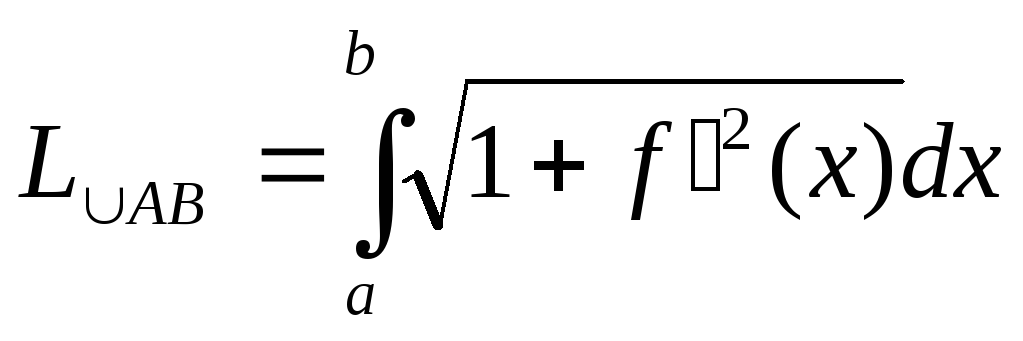- в прямоугольных координатах.

б) Пусть АВ задана своими параметрическими уравнениями: , тогда.

МЕТОДИКА 10. Логико – математический анализ теоретического материала темы

Основные понятия темы:

• Первообразная;

• Криволинейная трапеция;

• Интеграл функции (пределы интегрирования, знак интеграла, подынтегральная функция, переменная интегрирования).

Основные предложения темы:

• Признак постоянства функции;

• Теорема (основное свойство первообразных);

• Правила нахождения первообразных;

• Теорема (вычисление площадей криволинейных трапеций): .

• Если 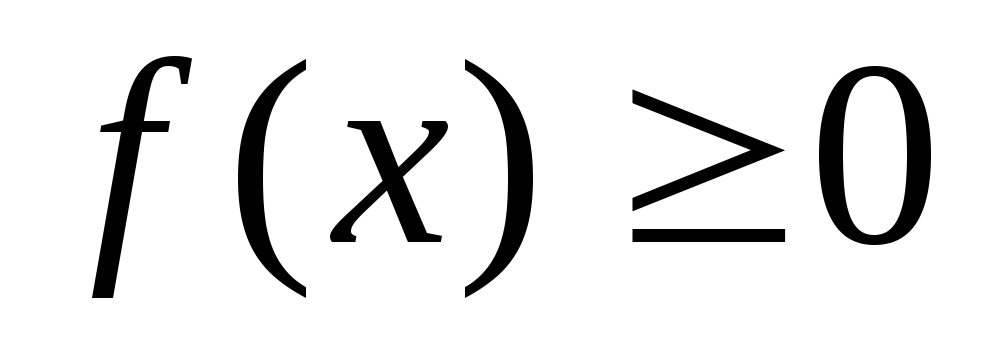на отрезке [a;b], то площадь S соответствующей криволинейной трапеции выражается формулой S= .

• Если F - первообразная для f на отрезке [a;b], то 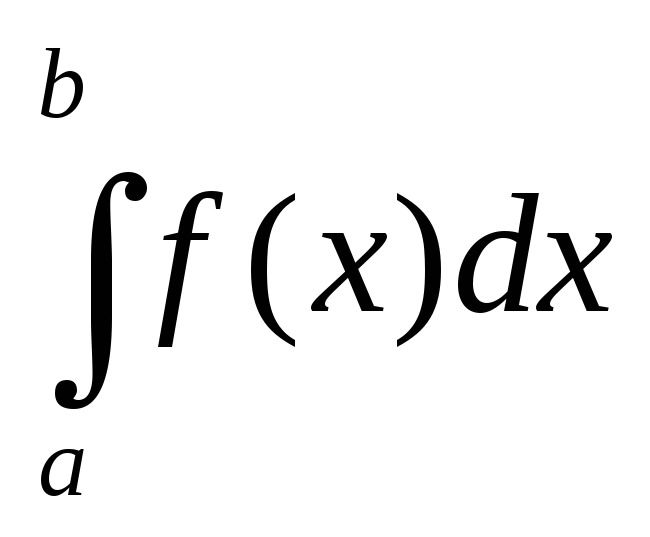=формула Ньютона – Лейбница. Она верна для любой функцииf, непрерывной на отрезке [a;b].

• Замечание: удобно расширить понятие интеграла, полагая по определению при , что.

• Геометрический смысл основного свойства первообразных: графики любых двух первообразных для функции получаются друг из друга параллельным переносом вдоль оси OY.

Результаты логико – математического анализа можно представить в виде таблицы:

Ранее изученный материал	Теоретический материал темы	Применение изученного материала
Площадь, свойства площади, формулы для вычисления площади. Производная функции, дифференциал функции, правила вычисления производных, производные физических величин. Функция, график функции, приращение функции.	Формула Ньютона – Лейбница Переменная интегрирования Подынтегральная функция Знак интеграла Пределы интегрирования (нижний и верхний) Интеграл функции Криволинейная трапеция Общий вид первообразных для функции Первообразная Признак постоянства функции Основное свойство первообразных Геометрический смысл основного свойства первообразных Правила нахождения первообразных Теорема о вычислении площадей криволинейных трапеций	В физике и геометрии: вычисление физических и геометрических величин с помощью интеграла Решение задач в этих дисциплинах

1. Место темы в программе, учебниках математики

Пропедевтика элементов математического анализа (производной и интеграла) проводится при изучении функций в основной школе.

Тема «Интеграл» изучается в 11 классе по учебнику Алгебра и начала анализа: Учеб.для 10-11 кл.общеобразоват.учреждений/Ш. А. Алимов, Ю. М. Колягин и др.-10-е изд.-М.:Просвещение, 2002

2. Виды планирования темы, примерная структура тематического плана

Тема	Подтема	Задачи	Теоретич. материал	Задачи в классе	Задачи дома	Повторение	С/Р	Формы контроля
Интеграл	Правила нахождения первообразных	Ввести правила нахождения первообразных, научить применять правило на практике	Таблица первообразных	988; 989(1,2,3); 992(1,2).	989(4,5,6); 990(1,2,3); 992(3,4).			Опрос, индивидуальная проверка
	Решение задач	Закрепить данные правила в процессе решения задач. Осуществить контроль за состоянием знаний и умений по теме.		993; 994(1,3); 995(1,2).	994(2,4); 995(3,4); 996.	998 (для сильных учащихся)		Проверка д/з, с/р.

3. Опишите технологический подход к планированию темы

Технологическая карта (педагогическая технология В.М.Монахова). Тема: Интеграл (11 класс).

Логическая структура учебного процесса	В1 Д1 В2 Д2
Целеполагание	Диагностика	Коррекция
В1. Знать определение криволинейной трапеции. Уметь распознавать к.т. и вычислять ее площадь.	С/р1. Вычислить площадь к.т., ограниченной линиями: y=x^3+1, y=0, x=0, x=2 y=cos x, y=0, x=0, x= y=x^2, y=0, x=0, x=3	Возможные ошибки: при выполнении рисунка (неверное изображение графиков функций); в нахождении первообразных; вычислительные, при вычислении S к.т.; Замечание: учебные задачи для коррекции составляются для предупреждения и устранения каждого вида ошибки.
В2. Знать формулу Ньютона – Лейбница, применять ее к вычислению S фигуры, ограниченной линиями. Уметь вычислять S фигуры.	С/р2. Вычислить интегралы:	Возможные ошибки: в нахождении первообразных; выбор неправильной фигуры для вычисления S. В применении формулы Ньютона - Лейбница
Дозирование самостоятельной деятельности учащихся
Удовлетворительно	Хорошо	Отлично
Вычислить площадь фигуры, ограниченной линиями: x=-1, x=2; x=3,y=0.	Вычислить площадь фигуры, ограниченной линиями: y=x^2-x-5, y=x-2 y=x^2+x-4, y=6-x^2	Вычислить площадь фигуры, ограниченной линиями: y=x^2, y=sin x,
Вычислить интегралы:	Вычислить интегралы:	Вычислить интегралы:

Билет № 11. Основные алгебраические структуры

Определения и примеры групп, колец и полей

Определение 1.1. Пусть G   и  – бинарная алгебраическая операция на G, т.е.  a, b  G ! a b  G. Алгебра (G, ) называется группой, если выполнены аксиомы:

(А 1):  a, b, c  G (a b) c = a (b c) (операция  ассоциативна)

(А 2):  e  G  a  G a e = a = e  a (существование нейтрального элемента)

(А 3):  a  G  a^–1  G a a^–1 = e = a^–1 a (существование симметричного элемента)

Примеры: 1. (Z , +), (Q , +), (R , +), (C , +).

2. (M_{m n} (F), +), (GL(n, F), ), где GL(n, F) = {A  M_nn (F) | |A|  0} – множество обратимых матриц.

3. (Z_n , +), (Z_n^ ,  ), где Z_n^ = { Z_n | Н.О.Д.(a, n) = 1} – множество обратимых вычетов.

4. (N, +) – не группа, т.к. нарушено свойство (А2).

Определение 1. 2. Группа (G, ) называется абелевой или коммутативной, если выполняется аксиома коммутативности:

(А 4):  a, b  G a  b = b  a

Единственная некоммутативная (неабелева) группа из вышеперечисленных – это мультипликативная группа обратимых матриц (GL(n, F), ) при n  2.

Определение 1.3. Пусть K   и +,  – две бинарные алгебраические операции на K, т.е.  a, b  K  ! a + b  K и  a, b  K  ! a b  K . Алгебра (K, +,  называется кольцом, если выполнены аксиомы I, II, III.

I. Аксиомы сложения: (K, +) – абелева группа, т.е. удовлетворяет аксиомам (А1), (А2), (А3), (А4). Нейтральный элемент кольца называется нулевым элементом и обозначается 0, а симметричный элемент к а по сложению – противоположным и обозначается – a .