6.2 Типовые законы распределения непрерывных случайных величин

6.2.1 Равномерное распределение

Равномерное распределение имеет непрерывная случайная величина Х, если ее плотность вероятности в некотором интервале а; b] постоянна, т.е. если все значения X в этом интервале равновероятны:

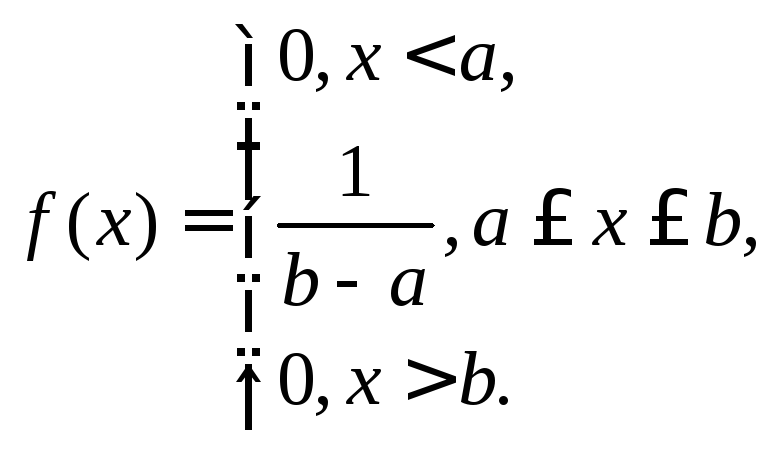
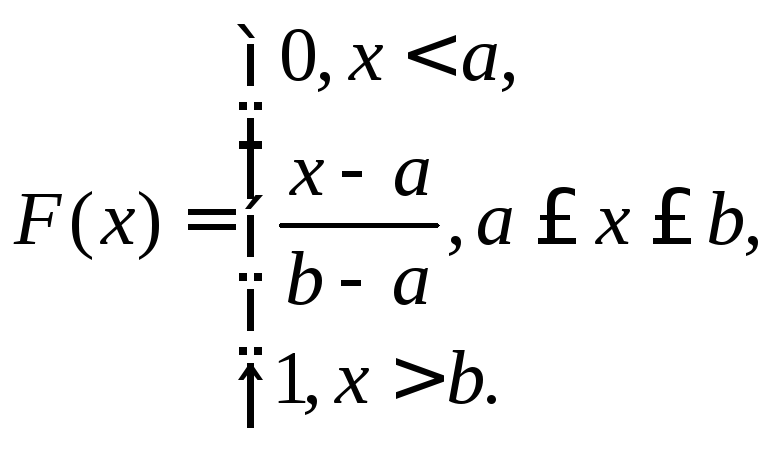(6.8)

Ниже приведены графики плотности и функции равномерного распределения при b=3 и a =1.

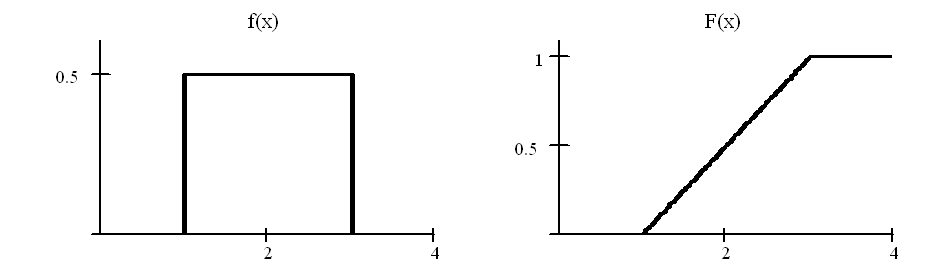
Числовые характеристики равномерно распределенной случайной величины:

. (6.9)

При необходимости определения параметров a и b по известным m_X, D_X используют следующие формулы:

(6.10)

Условия возникновения:

1) Случайная величина Х - ошибки округления при ограниченной разрядной сетке:

- округление до меньшего целого, ,

- округление до большего целого, ,

- округление до ближайшего целого, ,

где 1 – вес младшего разряда.

2) Случайная величина Х - погрешность считывания значений с аналоговой шкалы измерительного прибора, , где 1 – цена деления шкалы.

3) Генераторы псевдослучайных величин, например RANDOM, встроенные в языки программирования высокого уровня.

6.2.2 Экспоненциальное распределение

Экспоненциальное распределение имеет непрерывная случайная величина T, принимающая только положительные значения, если ее плотность вероятности и функция распределения равны:

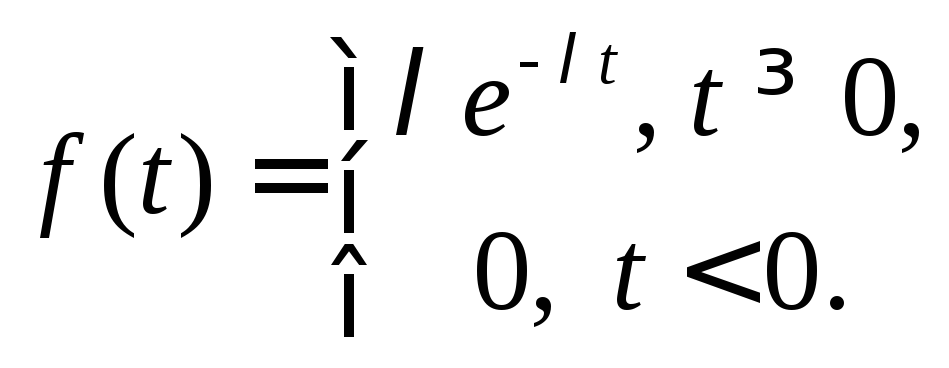
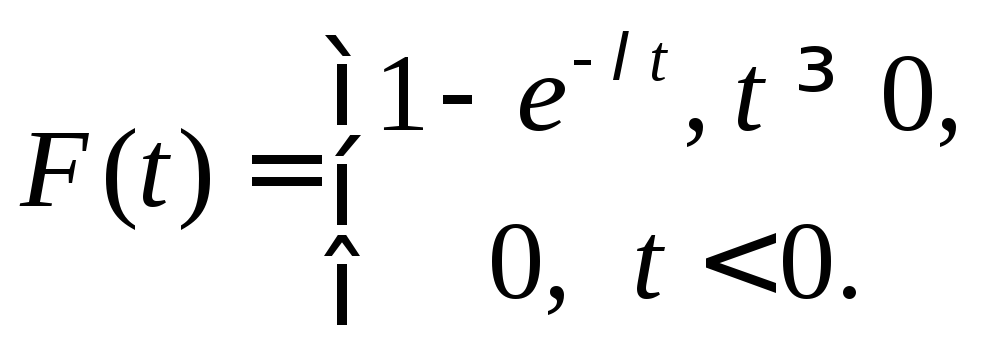(6.11)

где  – параметр распределения ( >0).

Ниже приведены графики плотности и функции экспоненциального распределения при  =1.

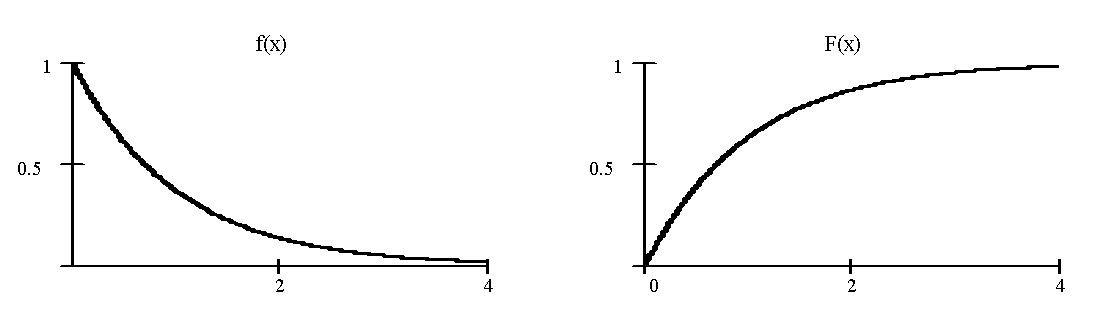
Числовые характеристики экспоненциальной случайной величины:

. (6.12)

Условия возникновения. Случайная величина T – интервал времени между двумя соседними событиями в простейшем или Пуассоновском потоке случайных событий, причем параметр распределения  – интенсивность потока.

6.2.3 Нормальное распределение

Нормальное распределение (распределение Гаусса) имеет непрерывная случайная величина Х, если ее плотность вероятности и функция распределения равны:

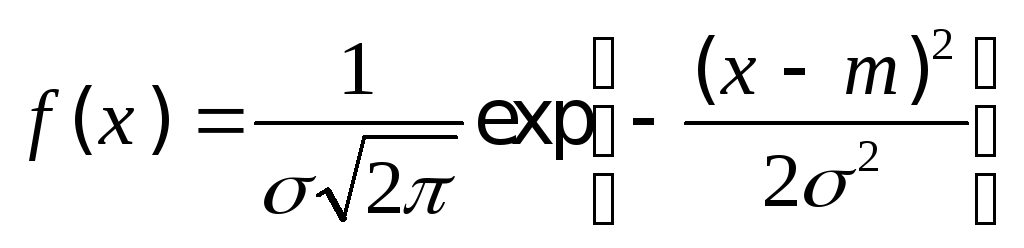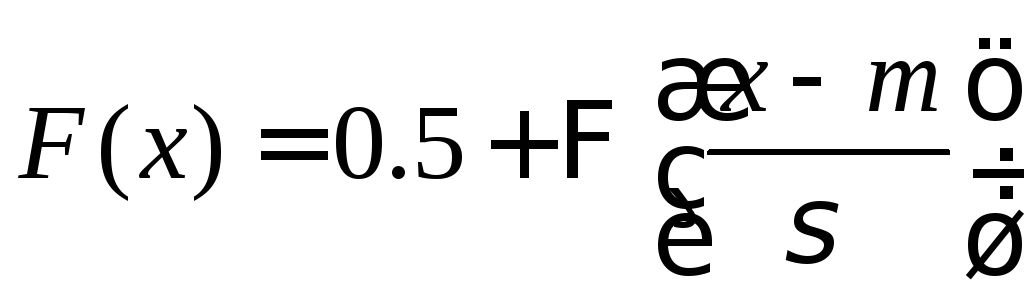,, (6.13)

где m, σ - параметры распределения ( σ >0),

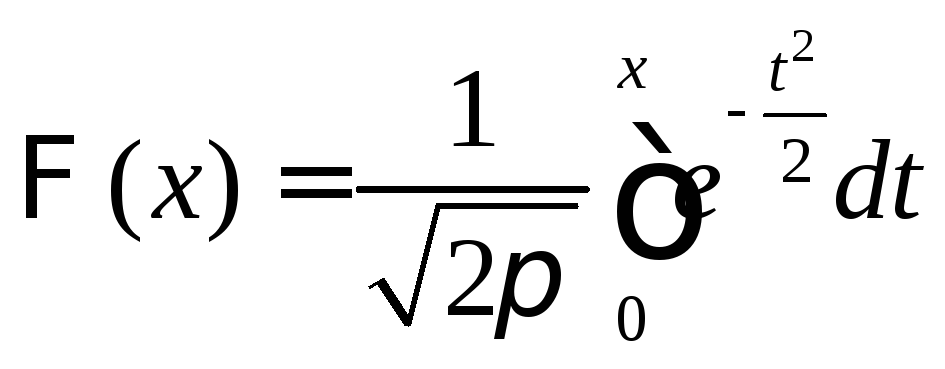—функция Лапласа.

Ниже приведены графики плотности и функции нормального распределения при m =1, σ =1.

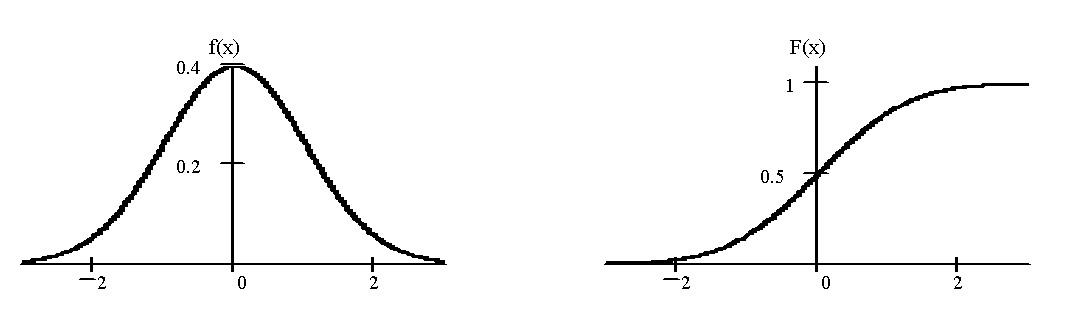Так как первообразная для в аналитическом виде не существует, то для вычисления значений функции распределения и вероятностей событий, связанных с нормальной случайной величиной используется табулированная функция Лапласа. При использовании таблицы значений функции Лапласа следует учитывать, что(- x) = - (x), (0) = 0, () = 0,5.

Числовые характеристики нормальной случайной величины:

; (6.14)

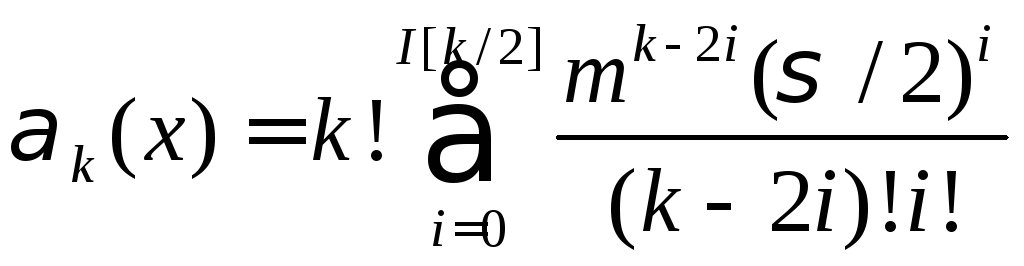; (6.15)

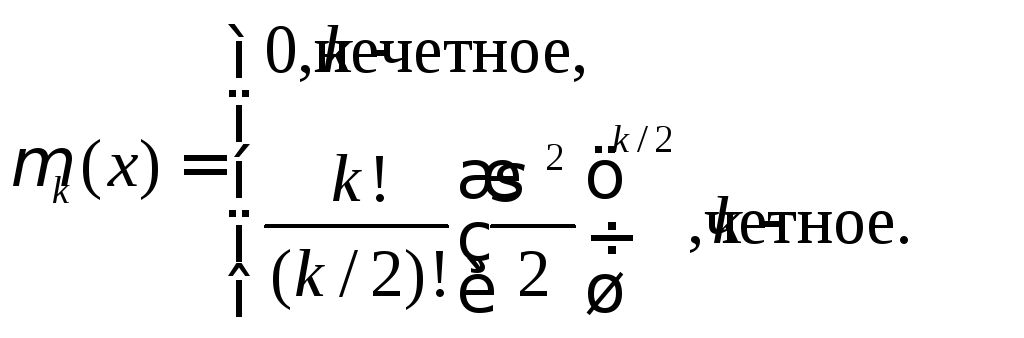(6.16)

Условия возникновения. Это наиболее часто встречающийся на практике закон распределения (см. лекцию 12; (центральную предельную теорему)). Например, нормальный закон распределения имеют:

- погрешности измерительных приборов; при этом откалибрированный прибор не имеет систематической погрешности, т.е. m=0, а величина σ определяется классом точности измерительного прибора;

- параметры радиоэлектронных компонентов (резисторов, конденсаторов, т.п.), причем m – номинальное значение, указанное на маркировке, а σ определяется классом точности.

Лекция 7

Пусть некоторая случайная величина Х подвергается детерминированному преобразованию , в результате которого получится величина Y, т.е. .

Очевидно, что величина Y будет случайной, и, как правило, необходимо определить закон распределения и/или числовые характеристики случайной величины Y по известному закону распределения величины Х и виду преобразования .