14.1.1 Оценка математического ожидания

Оценка математического ожидания. На основании теоремы Чебышева в качестве состоятельной оценки математического ожидания может быть использовано среднее арифметическое значений выборки , называемое выборочным средним:

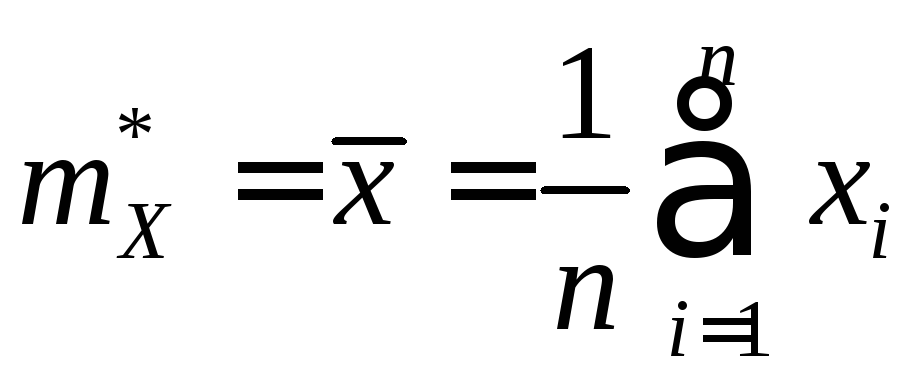. (14.5)

Определим числовые характеристики оценки x.

,

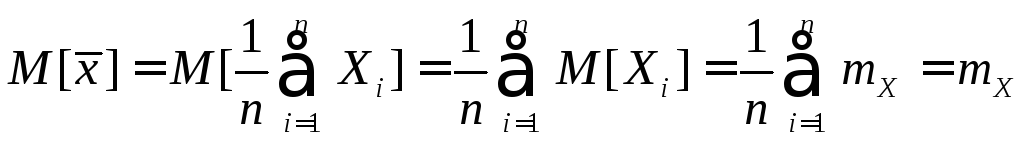т.е. оценка несмещенная.

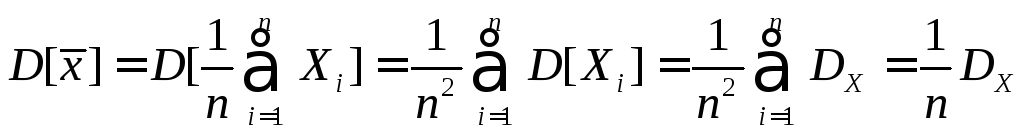. (14.6)

Оценка (14.5) является эффективной, т.е. ее дисперсия минимальна, если величина X распределена по нормальному закону.

14.1.2 Оценка начального момента

Состоятельная оценка начального момента k-го порядка на основании теоремы Чебышева определяется по формуле

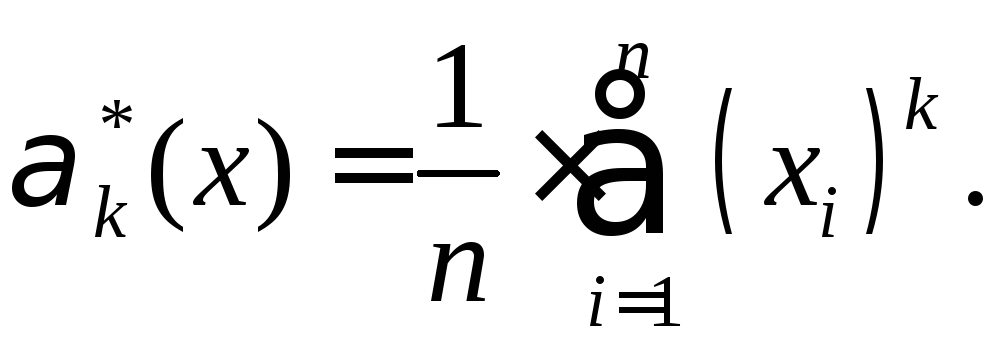(14.7)

14.1.3 Оценка дисперсии

Оценка дисперсии. В качестве состоятельной оценки дисперсии может быть использовано среднее арифметическое квадратов отклонений значений выборки от выборочного среднего:

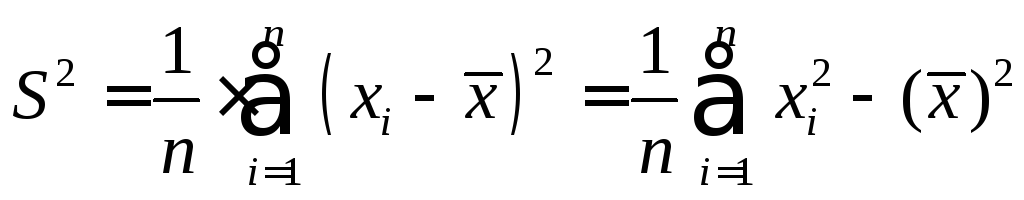. (14.8)

Определим математическое ожидание оценки S². Так как дисперсия не зависит от того, где выбрать начало координат, выберем его в точке m_X, т.е. перейдем к центрированным величинам:

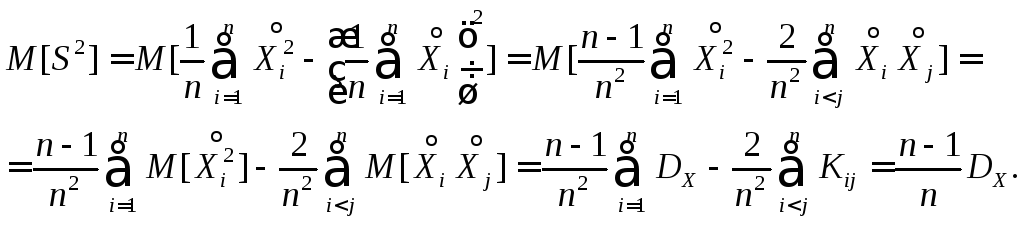
Ковариация , так как опыты, а следовательно, иХ_i  значение величины Х в i-м опыте  независимы. Таким образом, величина является смещенной оценкой дисперсии, а несмещенная состоятельная оценка дисперсии равна:

(14.9)

Дисперсия величины равна:

. (14.10)

Для нормального закона распределения величины X формула (14.10) примет вид

, (14.11)

для равномерного закона распределения –

. (14.12)

Состоятельная несмещенная оценка среднеквадратического отклоненияопределяется по формуле:

(14.13)

14.1.4 Оценка центрального момента

Состоятельная оценка центрального момента k-го порядка равна:

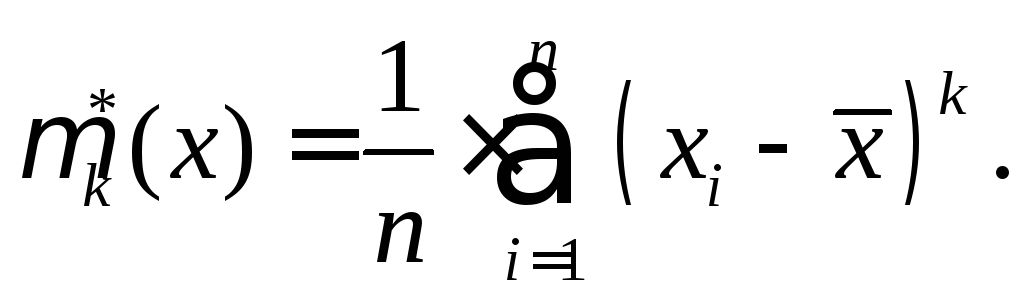(14.14)

14.1.5 Оценка вероятности

Оценка вероятности. На основании теоремы Бернулли несмещенная состоятельная и эффективная оценка вероятности случайного события A в схеме независимых опытов равна частоте этого события:

, (14.15)

где m - число опытов, в которых произошло событие A;

n - число проведенных опытов.

Числовые характеристики оценки вероятности равны:

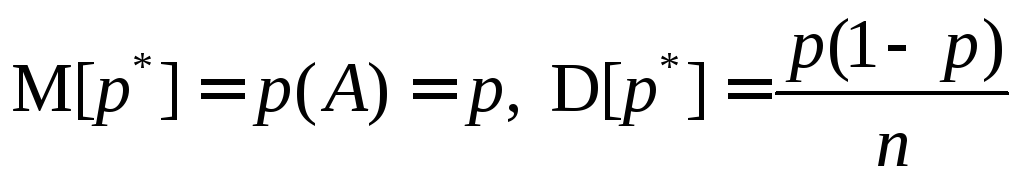. (14.16)

14.2 Оценка параметров распределения

Для вычисления оценок параметров распределения чаще всего применяются методы моментов и максимального правдоподобия.

Метод моментов. Пусть имеется выборка {x₁, ..., x_n} независимых значений случайной величины с известным законом распределения и m неизвестными параметрами . Необходимо вычислить оценки параметров . Последовательность вычислений следующая:

1. Получить аналитические выражения m начальных и/или центральных теоретических моментов

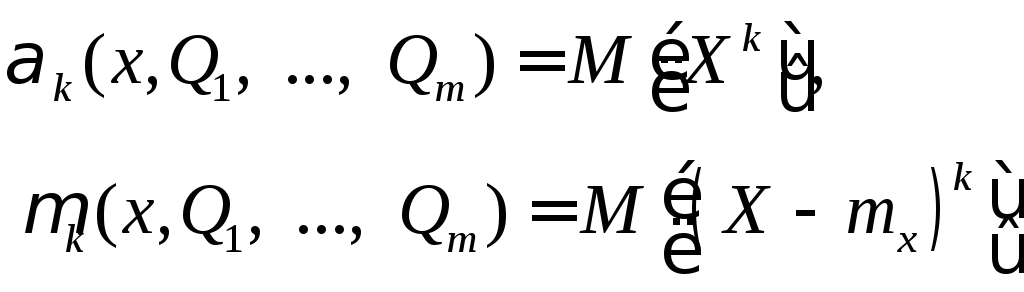. (14.17)

2. Определить m соответствующих оценок начальных и/или центральныхмоментов по формулам (14.7, 14.14).

3. Составить и решить относительно неизвестных параметров систему из m уравнений:

,

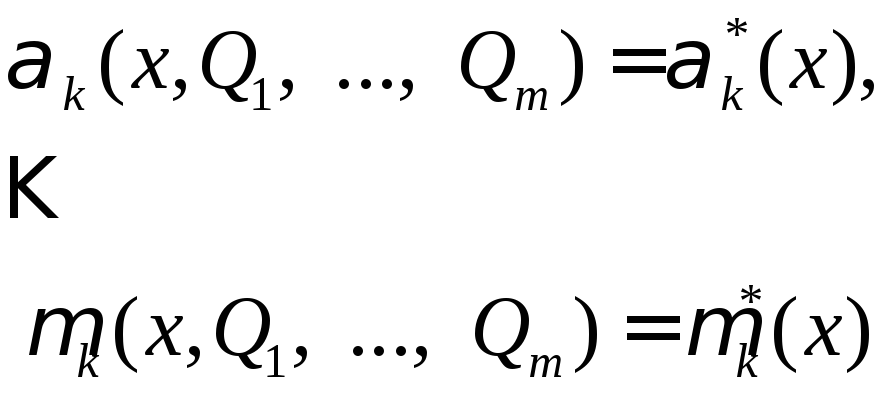в которых теоретические моменты приравниваются к точечным оценкам соответствующих моментов. Каждое уравнение имеет вид или. Найденные корни являются оценками неизвестных параметров.

Замечание. Часть уравнений может содержать начальные моменты, а оставшаяся часть - центральные.

Метод максимального правдоподобия. Согласно данному методу оценки получаются из условия максимума по параметрам положительной функции правдоподобия .

Если случайная величина X непрерывна, а значения x_i независимы, то

Если случайная величина X дискретна и принимает независимые значения x_i с вероятностями то функция правдоподобия равна

Система уравнений согласно этому методу может записываться в двух видах:

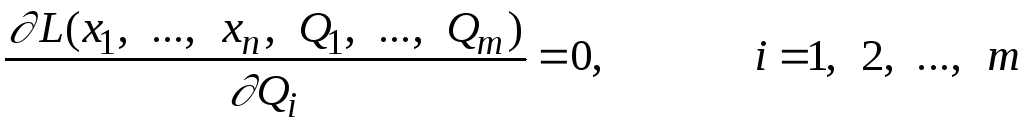(14.18)

или

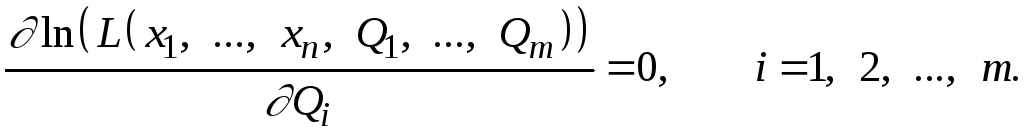(14.19)

Найденные корни выбранной системы уравнений являются оценками неизвестных параметров .