11.2.2 Теорема о дисперсии суммы

Теорема о дисперсии суммы случайных величин. Дисперсия суммы случайных величин равна сумме всех элементов корреляционной матрицы слагаемых:

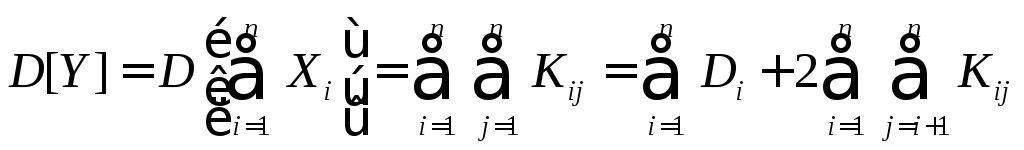. (11.7)

Доказательство:

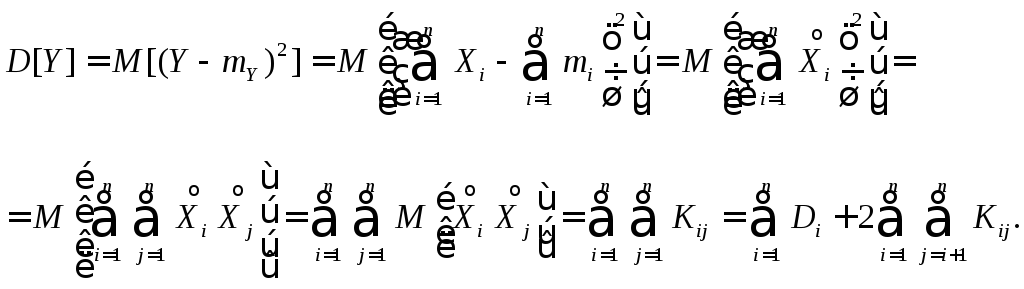
Следствие. Дисперсия суммы некоррелированных случайных величин равна сумме дисперсий этих величин, так как :

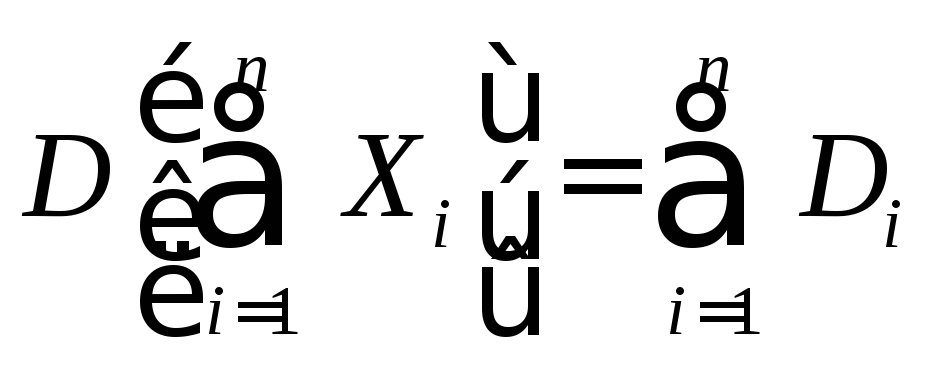. (11.8)

Если 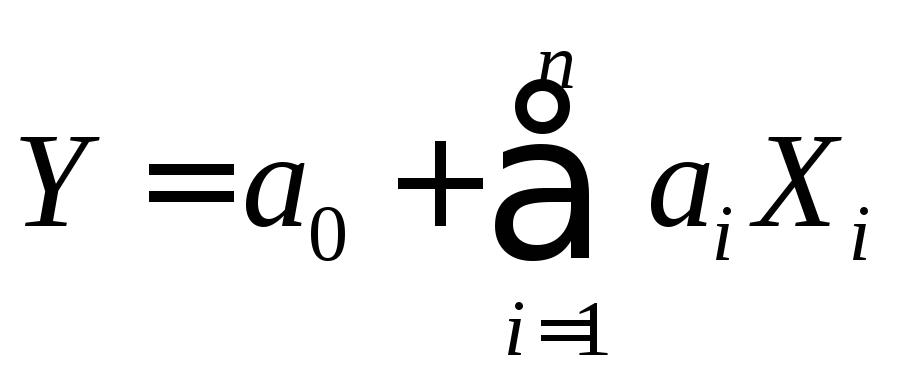,- не случайные коэффициенты, то дисперсияY равна:

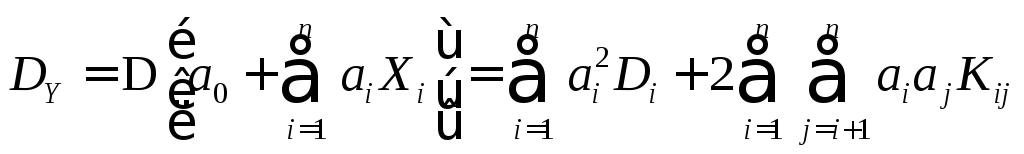. (11.9)

Это легко доказать, используя (11.7) и свойства дисперсии (D[c] = 0, D[X+c] = D_X, D[c×X] = c^2D_X).

Пример. Докажем, что абсолютная величина корреляционного момента двух случайных величин не превышает среднего геометрического их дисперсий:

или .

Введем в рассмотрение случайные величины и вычислим их дисперсии по формуле (11.9):

; .

Так как дисперсия всегда неотрицательна, то и . Таким образом, .

11.3 Числовые характеристики произведения случайных величин

Пусть 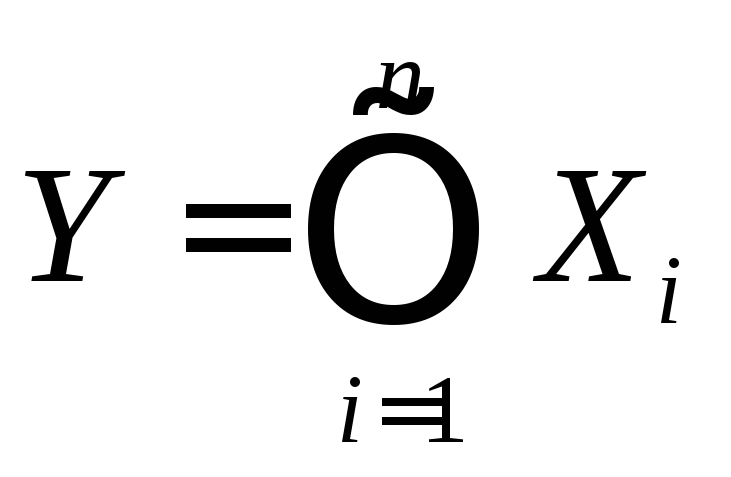, гдеХ₁ , Х₂ ,…Х_n - случайные величины с известными числовыми характеристиками:

- вектор математических ожиданий M=(m₁,m_2,…m_n);

- вектор дисперсий D=(D₁,D₂,…D_n);

- корреляционная матрица .

11.3.1 Теорема о математическом ожидании произведения

Теорема о математическом ожидании произведения случайных величин. Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс ковариация:

. (11.10)

Доказательство. По определению ковариация равна:

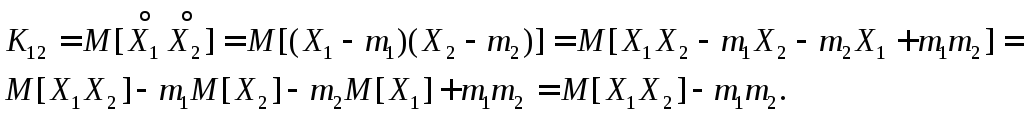Откуда следует формула (11.10).

Следствие. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:

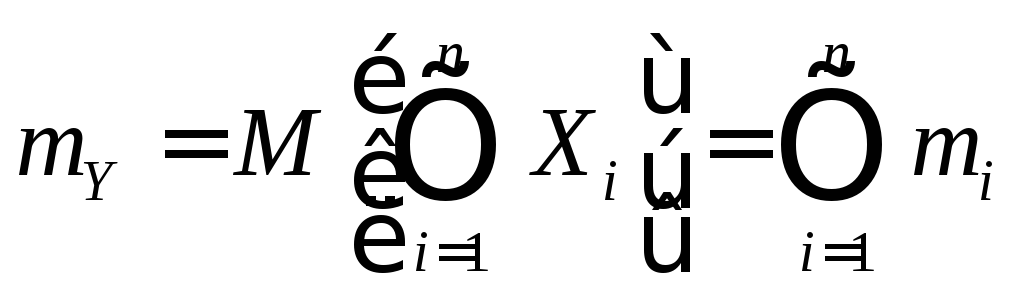(11.11)

Доказательство: Пусть n = 2. Для независимых случайных величин , тогда формула (11.10) примет вид .

Используя метод математической индукции, легко доказать, что (11.11) справедлива для любого n.

11.3.2 Теорема о дисперсии произведения

Теорема о дисперсии произведения случайных величин. Дисперсия произведения независимых случайных величин равна

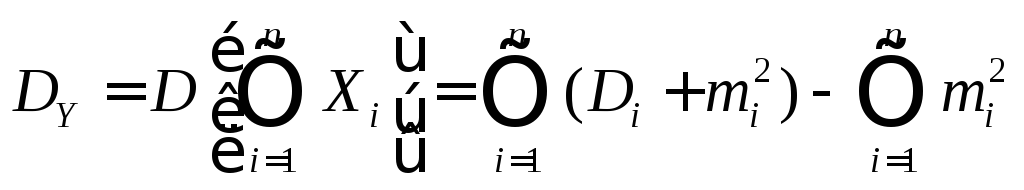(11.12)

Доказательство: По определению дисперсия равна

.

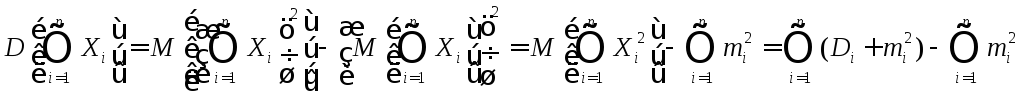Следствие. Дисперсия произведения независимых центрированных случайных величин равна произведению дисперсий этих величин:

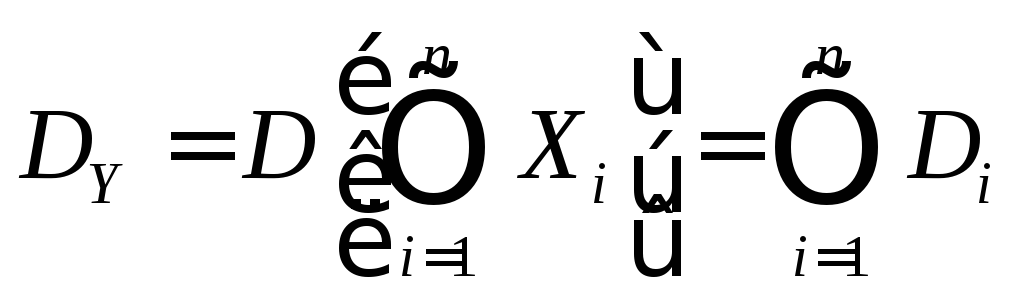. (11.12)

Лекция 12

12.1 Закон больших чисел

Пусть проводится некоторый опыт, в котором нас интересует значение случайной величины Х. При однократном проведении опыта нельзя заранее сказать, какое значение примет величина Х. Но при n-кратном (n > 100...1000) повторении «среднее» (среднее арифметическое) значение величины Х теряет случайный характер и становится близким к некоторой константе.

Закон больших чисел – совокупность теорем, определяющих условия стремления средних арифметических значений случайных величин к некоторой константе при проведении большого числа опытов.

12.1.1 Неравенство Чебышева

Неравенство Чебышева. Для любой случайной величины X с математическим ожиданием m_X и дисперсией D_X выполняют следующее неравенство:

, (12.1)

где ε > 0.

Доказательство. Рассмотрим вероятность :

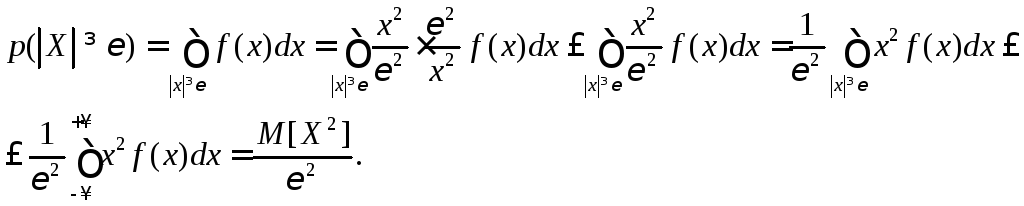
Таким образом, . Заменив нецентрированную величину X на центрированную , получим .

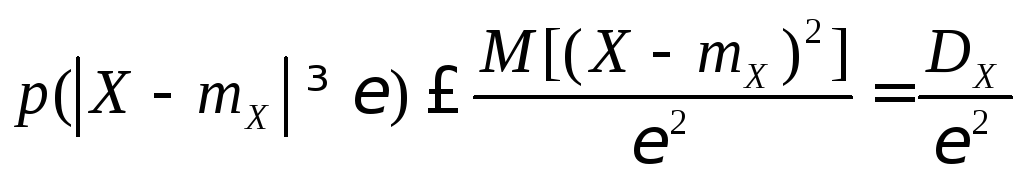Пример. Определим вероятность, что случайная величина примет значение за пределами интервала 3σ_X. Полагаем в неравенстве Чебышева , имеем:

.

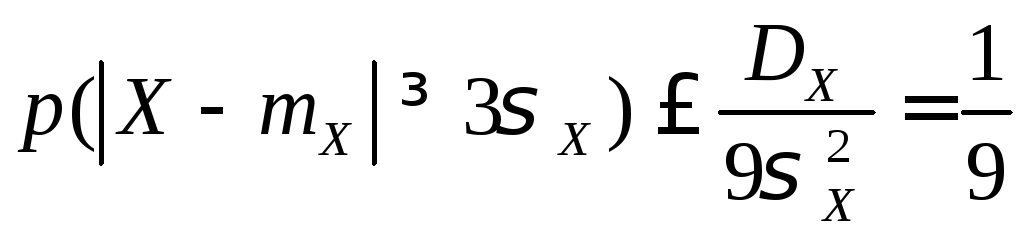Неравенство Чебышева дает только верхнюю границу вероятности данного отклонения. Значение вероятности быть выше этой границы (1/9) не может ни при каком законе распределения. Таким образом, правило 3σ_X выполняется с вероятностью не меньшей чем 8/9.

Сходимость по вероятности. Последовательность случайных величин X_n сходится по вероятности к величине a, , если при увеличении n вероятность того, что X_n и a будут сколь угодно близки, неограниченно приближается к единице:

где , - произвольно сколь угодно малые положительные числа.

Одна из наиболее важных форм закона больших чисел – теорема Чебышева, она устанавливает связь между средним арифметическим наблюдаемых значений случайной величины и ее математическим ожиданием.