7.1. Закон распределения функции случайного аргумента

В случае, если Х - дискретная случайная величина с известным рядом распределения вероятностей:

xi	x1	x2	…	xn
pi	p1	p2	…	pi

то определение ряда вероятностей Y не составит сложности. Так как , то значениебудет появляться вероятностьюp_i :

yi	(x1)	(x2)	…	(xn)
pi	p1	p2	…	pn

(*)

Из (*) путем упорядочивания и объединения одинаковых значений получаем ряд распределения случайной величины Y:

yi	y1	y2	…	ym
pj	p1	p2	…	pm

Если Х – непрерывная случайная величина с известной плотностью вероятности , то алгоритм получения закона распределениязависит от вида. Рассмотрим участок оси абсцисс [а,b], на котором лежат все возможные значения величины Х, т.е. , в частном случае. Способ решения поставленной задачи зависит от поведения функции на участке [а,b]: монотонна она на этом участке или нет.

7.1.1 Монотонно возрастающая функция

Пусть - монотонно возрастающая функция. Определим функцию распределения случайной величины У.

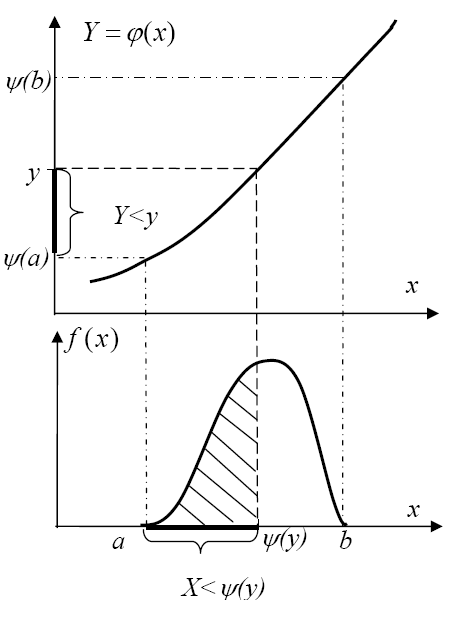
По определению она равна

,

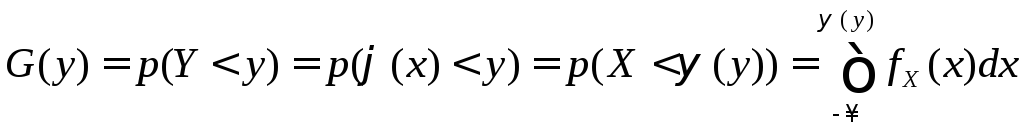где (y) - обратная функция (x).

Для выполнения условия необходимо и достаточно, чтобы случайная величина Х попала на участок оси абсцисс от а до (y). Таким образом, функция распределения Y для аргумента X, распределенного в интервале [a,b], равна:

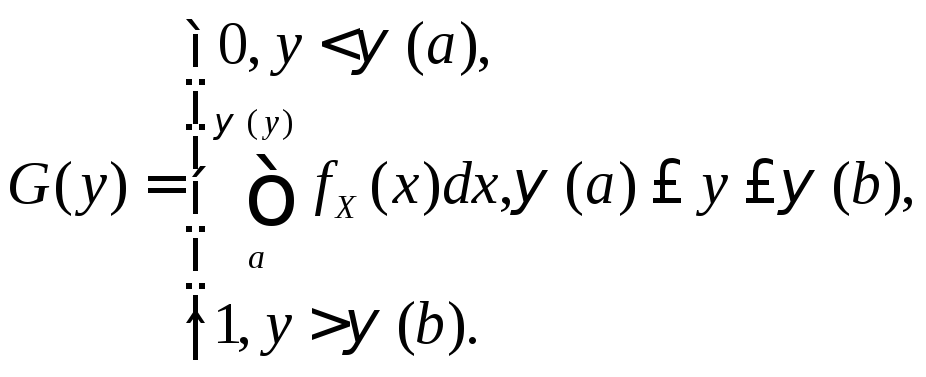
7.1.2 Монотонно убывающая функция

Пусть - монотонно убывающая функция. Определим функцию распределения случайной величиныY.

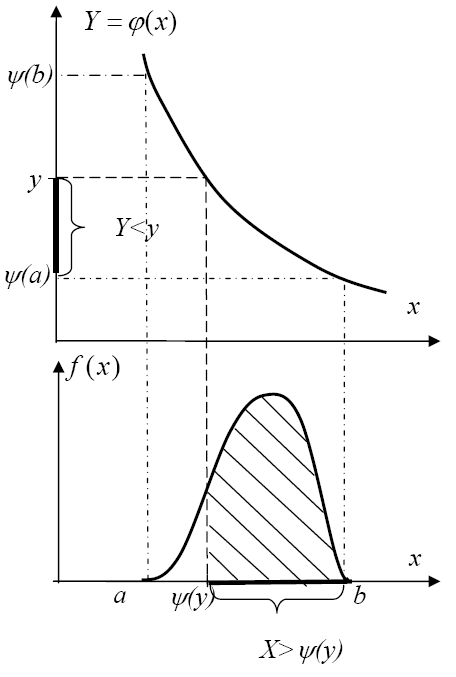
По определению она равна

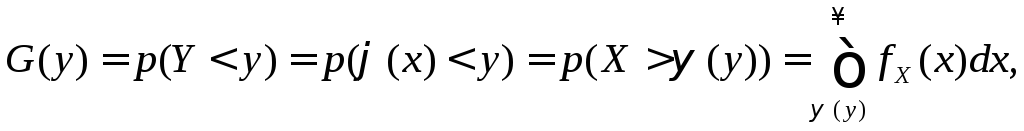
где (y) - обратная функция (x).

Для выполнения условия необходимо и достаточно, чтобы случайная величина Х попала на участок оси абсцисс от х = (y) до b. Таким образом, функция распределения Y для аргумента X, распределенного в интервале [a,b], равна

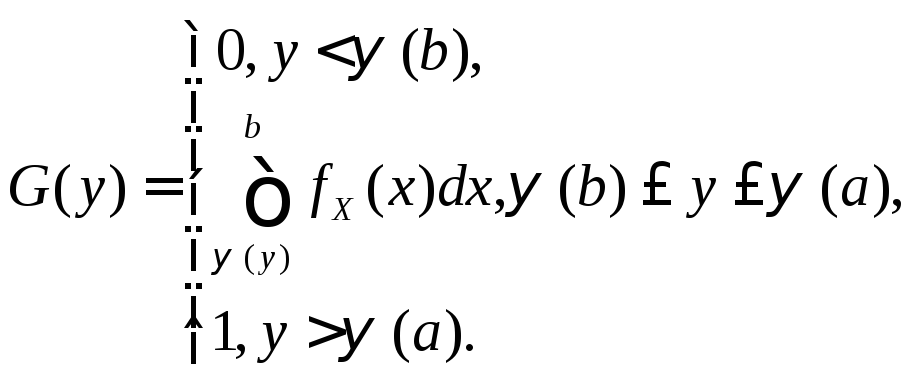
Плотность вероятностей случайной величины для любого монотонного случая имеет следующий вид:

(7.1)

Пример. Пусть случайная величина Х имеет нормальный закон распределения ,. Найти

Функция строго монотонна, дифференцируема и имеет обратную.Воспользуемся формулой (7.1). Так как

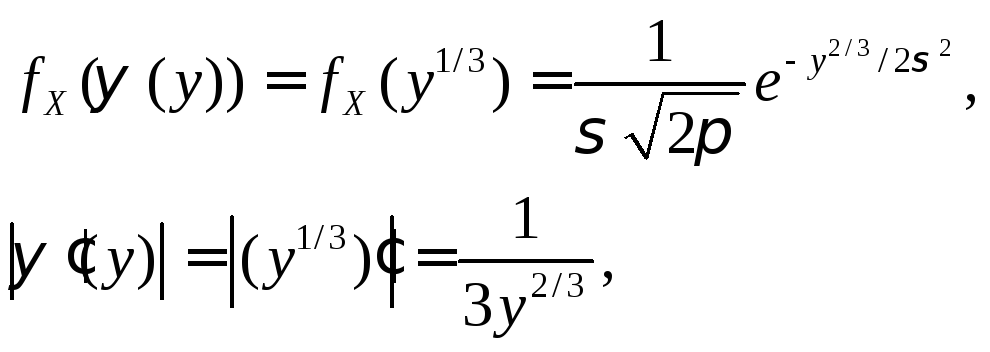
то искомая плотность распределения функции :

.

7.1.3 Немонотонная функция

Пусть - немонотонная функция. Алгоритм получения закона распределения приведен ниже.

1. Построить график и определить диапазон значений .

2. Диапазон Y разбить на M интервалов, в каждом из которых одинаковая степень неоднозначности k_i, i=1,2, .. M:

.

Степень неоднозначности k_i – число значений Х, соответствующих одному значению Y, или число обратных функций для данного интервала _j(у), j=1… k_i.

3. Определить обратные функции _j(у) = ^-1 (х) и вычисляется _j'(у).

В общем случае число обратных функций _j(у) в i-м интервале равко k_i

4. Определить плотность вероятностей по следующей формуле:

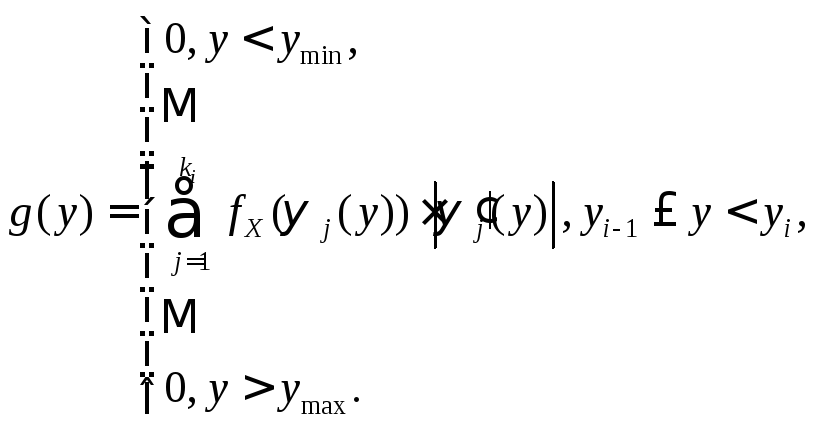(7.2)

В частном случае, когда обратные функций одинаковы для всех интервалов, формула (7.2) принимает вид

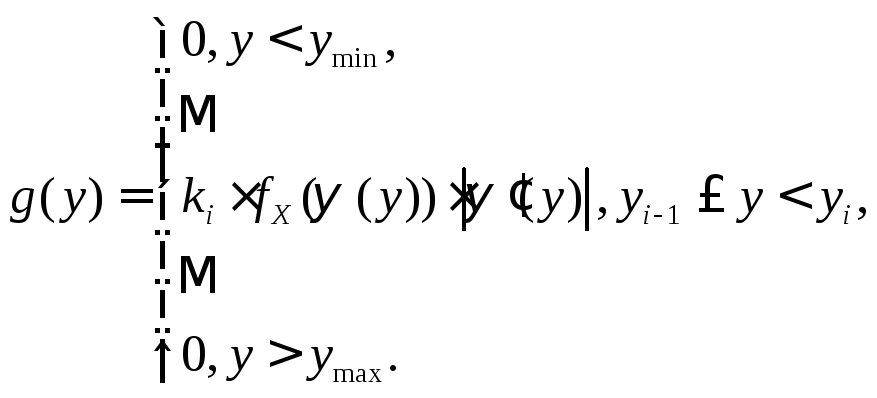, (7.3)

а если величина Х равномерно распределена в интервале a, b, т.е. ее плотность равна 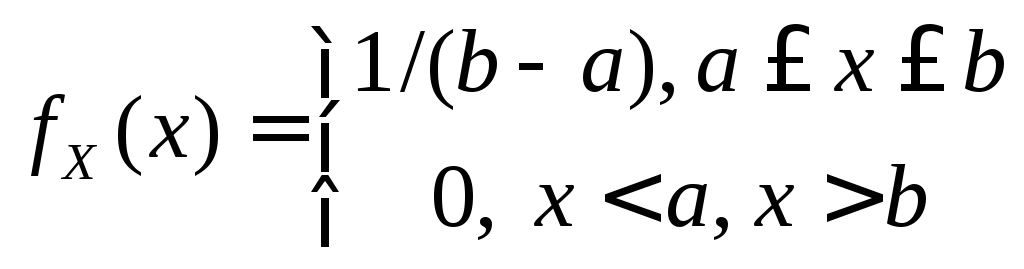, то выражение дляg(у) можно представить как

(7.4)

7.2 Числовые характеристики функции случайного аргумента

Пусть Y = (х), где X – случайная величина с известным законом распределения, и необходимо определить числовые характеристики Y. В том случае, когда закон распределения Y определен (см. выражения (7.1)  (7.4)), то числовые характеристики Y легко вычислить по формулам (5.1)  (5.7). Однако, если закон распределения величины Y в явном виде не нужен, а необходимы только ее числовые характеристики, применимы следующие формулы.

Если Х – дискретная случайная величина с известным рядом распределения вероятностей, то

; (7.5)

; (7.6)

; (7.7)

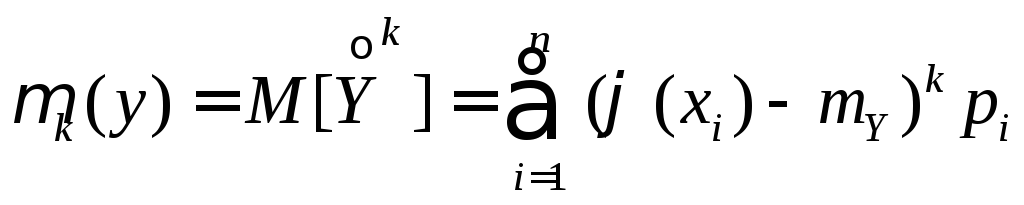. (7.8)

Если Х – непрерывная случайная величина с известной плотностью вероятностей f(x), то формулы принимают вид

; (7.9)

; (7.10)

; (7.11)

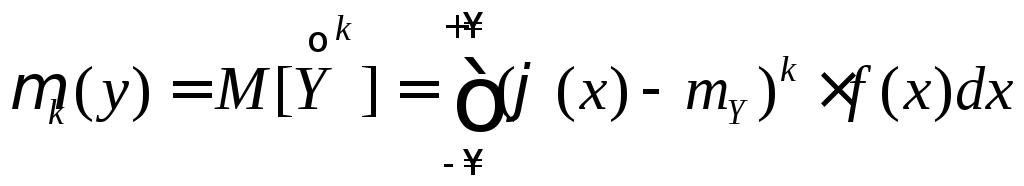. (7.12)