10.3 Многомерные случайные величины

Совокупность произвольного числа n одномерных случайных величин Х_i, i = 1,…,n, которые принимают значение в результате проведения одного и того же опыта, называется n-мерной случайной величиной (Х₁, Х₂, …Х_n). Ее можно интерпретировать как случайную точку или случайный вектор в n-мерном пространстве.

Полной характеристикой n-мерной случайной величины (Х₁, Х₂, …Х_n) является n-мерный закон распределения, который может быть задан функцией распределения или плотностью вероятности.

10.3.1 Функция распределения

Функцией распределения n-мерной случайной величиной (Х₁, Х₂, …Х_n) называется вероятность выполнения n неравенств вида Х_i <x_i:

. (10.6)

Функцию распределения любой частной системы из величин, входящих в систему, можно получить, если положить все остальные аргументы n-мерной функции распределения равными бесконечности.

10.3.2 Плотность распределения

Плотностью распределения n-мерной случайной величиной (Х₁, Х₂, …Х_n) называется n-я смешанная частная производная функции , взятая один раз по каждому аргументу:

. (10.7)

Она обладает следующими свойствами:

1. f(x₁…x_n) 0.

2. Условие нормировки:

(10.8)

3. Плотности распределения меньшего порядка могут быть получены путем интегрирования n-мерной плотности распределения по ненужным переменным. Например, одномерная плотность распределения величины Х_к равна:

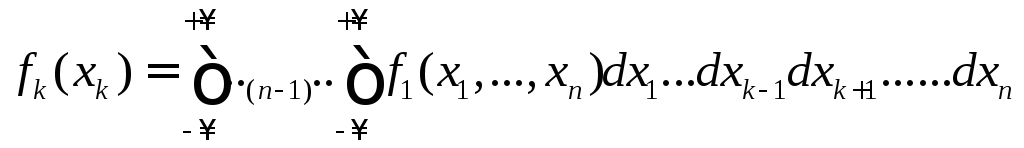(10.9)

4. Вероятность попадания случайной точки (Х₁, Х₂, …Х_n) в пределы n-мерной области D равна n-кратному интегралу по этой области:

(10.10)

Случайные величины (Х₁, Х₂, …Х_n) называются независимыми, если закон распределения каждой частной системы, выделенной из системы (Х₁, Х₂, …Х_n), не зависит от того, какие значения приняли остальные случайные величины.

Плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему: .

10.3.3 Числовые характеристики

Основные числовые характеристики n-мерной случайной величиной (Х₁, Х₂, …Х_n) следующие.

1. Вектор математических ожиданий M=(m₁,m_2,…m_n):

(10.11)

2. Вектор дисперсий D=(D₁,D₂,…D_n)

(10.12)

3. Корреляционная матрица, характеризующая попарную корреляцию всех величин, входящих в систему:

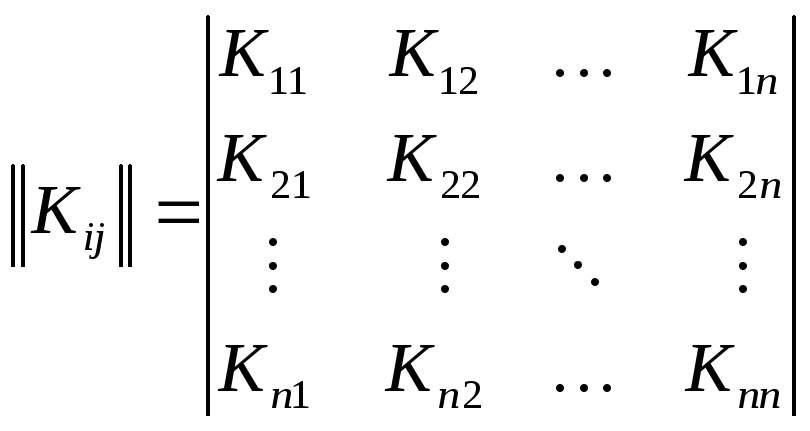
где

. (10.13)

Данная матрица является симметричной () и включает в себя вектор дисперсий, так какК_ii = D_i

4. Матрица коэффициентов корреляции:

,

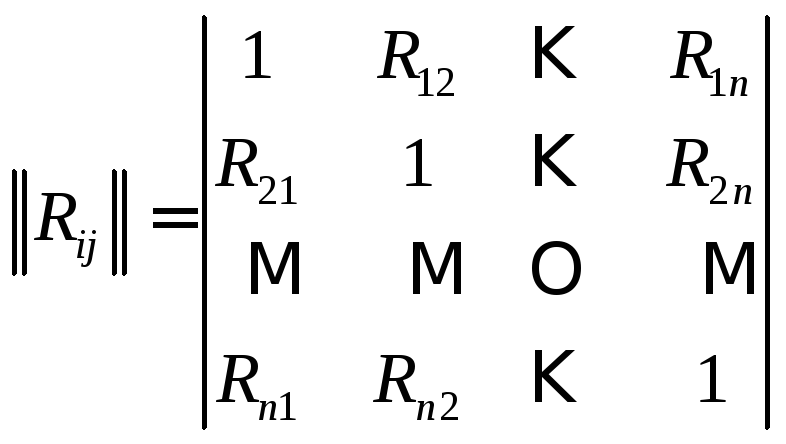где

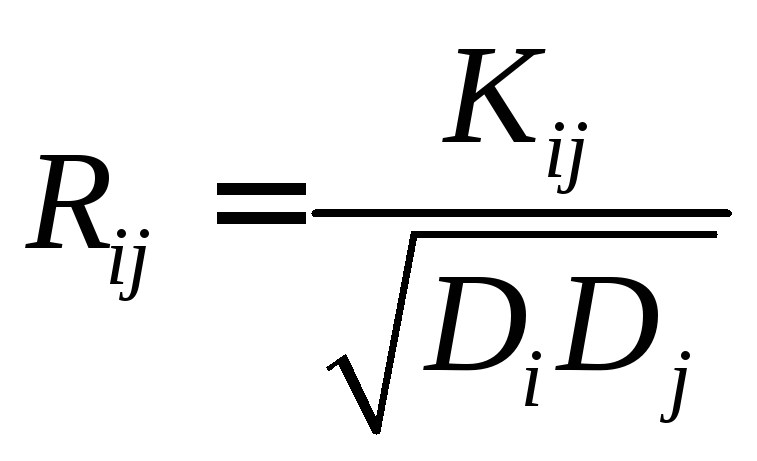. (10.14)

Матрица квадратная и симметричная.

Лекция 11

11.1 Числовые характеристики функции многих переменных

Пусть Y = (x₁ , x₂ ,…,x_n), где Х₁ , Х₂ ,…Х_n - случайные величины с известной совместной n-мерной плотностью вероятностей.

Начальные моменты величины Y определяются по формуле

, (11.1)

а центральные моменты  по формуле

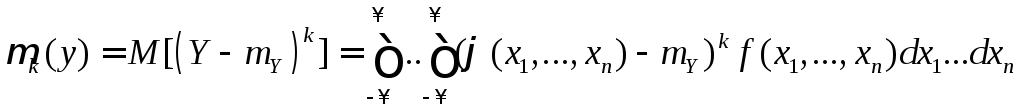, (11.2)

причем

, (11.3)

. (11.4)

В случае, когда совместная плотность вероятности аргументов неизвестна, а известны числовые характеристики аргументов, то задача определения числовых характеристикY разрешима только для определения классов функций .

11.2 Числовые характеристики суммы случайных величин

Пусть , гдеХ₁ , Х₂ ,…Х_n - случайные величины с известными числовыми характеристиками:

- вектор математических ожиданий M=(m₁,m_2,…m_n);

- вектор дисперсий D=(D₁,D₂,…D_n);

- корреляционная матрица .

11.2.1 Теорема о математическом ожидании суммы

Теорема о математическом ожидании суммы случайных величин. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:

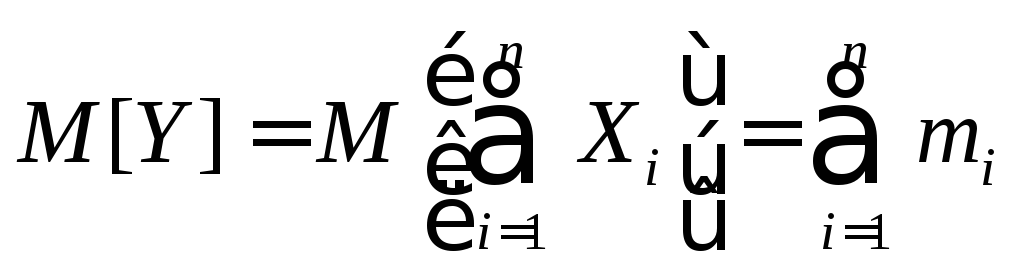. (11.5)

Доказательство. Пусть n = 2, т.е. Y = Х₁ + Х₂ и предположим, что слагаемые непрерывные случайные величины с некоторой совместной плотностью распределения . Тогда

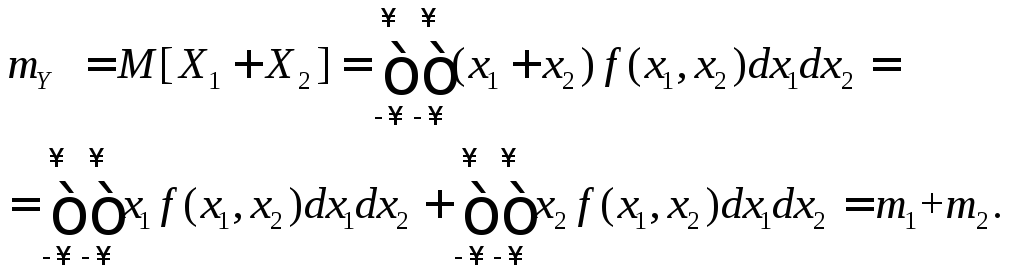
Аналогично и для дискретных слагаемых. Используя метод математической индукции, легко доказать, что теорема справедлива для любого n.

Если 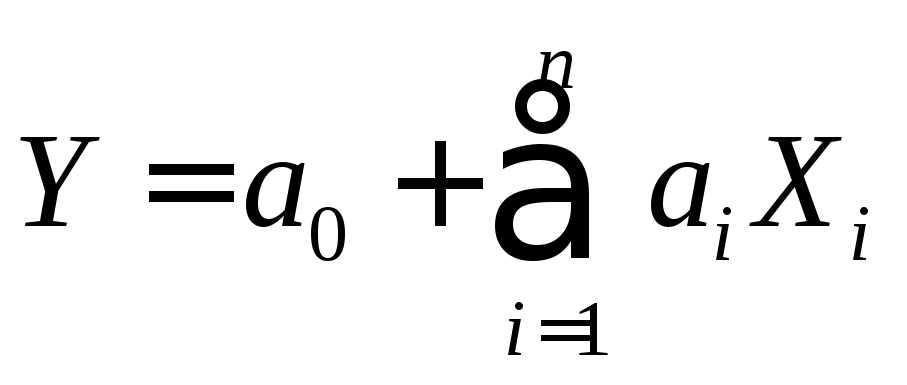, где- не случайные коэффициенты, то математическое ожиданиеY равно:

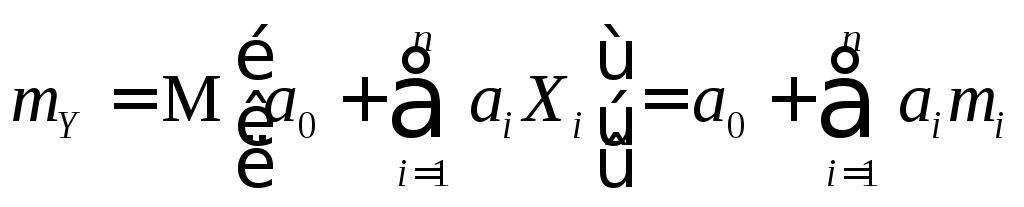; (11.6)

Это легко доказать, используя (11.5) и свойства математического ожидания (M[c] = c, M[X+c] = ,M[c×X] = ).